Square & Square root of 10

Square of 10

10² (10×10) = 100

The square of 10 is the result of multiplying 10 by itself, denoted as 10^2 or 10 * 10. The prefix “square” indicates that the number is multiplied by itself, while the suffix “of” specifies the number being squared, in this case, 10. Therefore, the square of 10 is 100.

Square Root of 10

√10 = 3.16227766017

The square root of 10 is an important mathematical concept, representing the value that, when multiplied by itself, equals 10. This value lies between 3 and 4, as 3^2 equals 9 and 4^2 equals 16. However, it is not a whole number, nor can it be expressed as a simple fraction. Instead, it is an irrational number, meaning its decimal representation goes on indefinitely without repeating. The approximate value of the square root of 10 is approximately 3.16227766017.

Square Root of 10: 3.16227766017
Exponential Form: 10¹/² or 10⁰.⁵
Radical Form: √10

Is the Square Root of 10 Rational or Irrational?

The square root of 10 is an irrational number.

• A rational number can be written in the form p/q, where p and q are integers and q is not equal to zero. Rational numbers include integers, fractions, and terminating or repeating decimals.
• An irrational number is a type of real number that cannot be expressed as the ratio of two integers. It cannot be written as a fraction where both the numerator and denominator are whole numbers.

The square root of 10 is an irrational number. It cannot be expressed as a simple fraction of two integers. When we calculate the square root of 10, we find that its decimal representation is non-repeating and non-terminating. This characteristic distinguishes irrational numbers from rational numbers, which can be expressed as fractions. The square root of 10 falls into the category of irrational numbers because it cannot be written in the form a/b where a and b are integers and b is not zero. Therefore, the square root of 10 is classified as an irrational number due to its unique decimal representation.

Methods to Find Value of Root 10

Finding the exact value of the square root of 10 (√10) is challenging due to its irrational nature, meaning its digits continue infinitely without repeating. However, several methods can approximate its value with increasing accuracy:

1. Prime Factorization Method: Decompose 10 into its prime factors (2 × 5), then find the square roots of each prime factor and multiply them together to obtain the square root of 10.
2. Estimation Method: Begin with a range based on nearby perfect squares (e.g., √9 = 3 and √16 = 4), then refine guesses within this range until reaching a satisfactory approximation of √10.
3. Using Calculators or Software: Utilize calculators or mathematical software equipped with functions to compute the square root of 10 directly, providing accurate results efficiently.
4. Iteration Method: Employ iterative techniques like the Newton-Raphson method to iteratively refine initial guesses of √10 until achieving a desired level of precision.
5. Table Lookup: Refer to mathematical tables or online resources containing pre-calculated values of square roots to find an approximate value for √10.

Square Root of 10 by Long Division Method

1. Separate Digits: Since 10 is a whole number, there are no digits after the decimal point. Therefore, we can separate 10 into pairs of digits as 10.
2. Initial Guess: Begin with an initial guess for the square root. Given that 10 lies between 3^2 = 9 and 4^2 = 16, we start with 3.
3. Divide and Average: Divide 10 by the initial guess (3). This yields 3.33. Next, average this result with the initial guess: (3 + 3.33) ÷ 2 ≈ 3.17. This becomes our new guess.
4. Repeat Process: Now, divide 10 by the new guess (3.17). The result is approximately 3.155. Average this result with the previous guess to obtain a new guess of about 3.162.
5. Continue Iterating: Keep repeating the division and averaging steps until the digits after the decimal point stop changing significantly.

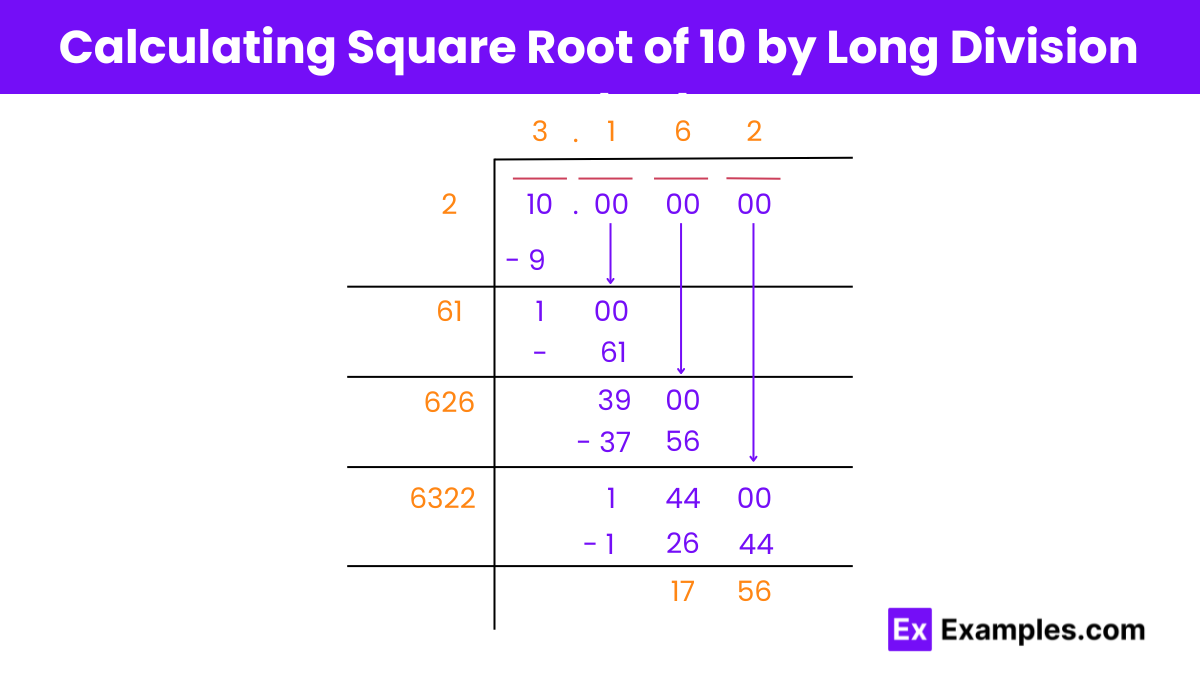
By following this method, we find that the square root of 10 is approximately 3.162. This approach provides a systematic way to approximate square roots using long division.

FAQ’S

Is √ 10 a real number?

Yes, √10 is a real number.The square root of 10 (√10) is a real number because it represents a valid solution on the real number line.

Is 10 an integer yes or no?

Yes, 10 is an integer. An integer is a whole number that can be positive, negative, or zero, and 10 falls under the category of positive integers because it is a whole number greater than zero.

What is the square root of 10 between?

The square root of 10 is between 3 and 4. It is approximately 3.16227766017. This irrational number falls between the perfect squares of 3 (which is 9) and 4 (which is 16), showing that its value lies between those two integers on the number line.