Square & Square Root of 113
Square & Square Root of 113
Square of 113
The square number of 113 is calculated by multiplying 113 by itself, resulting in 12,769. This square number exemplifies the fundamental concept of squaring in mathematics, showcasing the growth in magnitude when numbers are multiplied by themselves.
Square Root of 113
The square root of 113, an irrational number, is approximately 10.63014581273465. It represents the number that, when multiplied by itself, equals 113. Understanding square roots illuminates mathematical principles, offering insights into numerical relationships and facilitating problem-solving across various disciplines.
Is the Square Root of 113 Rational or Irrational?
A rational number can be expressed as the quotient of two integers, where the denominator is not zero.
An irrational number cannot be expressed as a fraction of two integers, and its decimal representation is non-repeating and non-terminating.
Method to Find Value of Root 113
1. Prime Factorization Method
- Decompose 113 into its prime factors, but since 113 is a prime number, its prime factorization is 113 itself.
2. Long Division Method
- Set up the long division by grouping digits in pairs, starting from the decimal point.
- Find the largest integer whose square is less than or equal to 113.
- Proceed with the division process, refining the quotient until the desired level of accuracy is reached.
3. Using a Calculator
- Input √113 into a scientific calculator to obtain an approximation of the square root.
4. Newton’s Method (Iterative)
- Start with an initial guess for the square root.
- Use the iterative formula to refine the approximation until reaching the desired level of accuracy.
5. Using a Table of Squares
- Refer to mathematical tables listing square roots of numbers and find the closest approximation for √113.
6. Continued Fractions
- Express √113 as a continued fraction, which can provide rational approximations.
7. Binomial Expansion
- Expand a binomial expression involving √113 to obtain a series approximation.
Square Root of 113 by Long Division Method
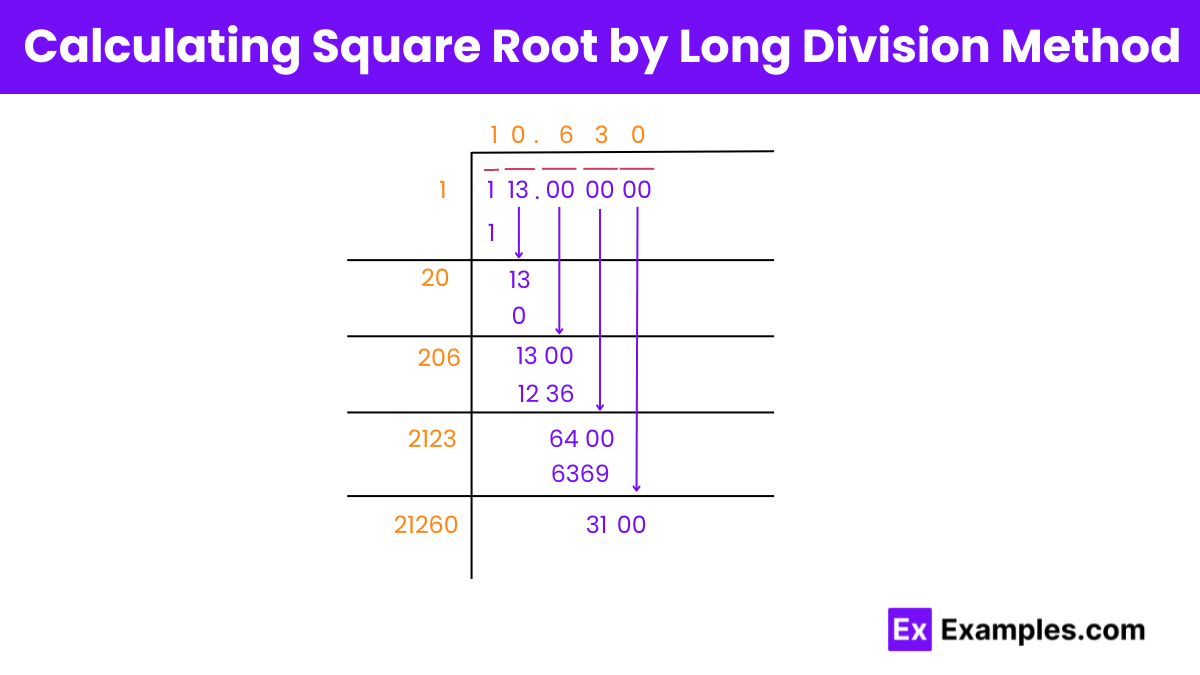
Step 1: Pair the digits of 113, starting from the one’s place, with a horizontal bar to indicate the pairing.
Step 2: Find the largest number whose square is less than or equal to 1, which is 1.
Step 3: Multiply the quotient by 2 to get the starting digit of the new divisor, which is 2.
Step 4: Place 0 at the one’s place of the new divisor, resulting in 20. The obtained answer is 13, and we bring down 00.
Step 5: Multiply the current quotient (10) by 2 to get 20, the starting digit of the new divisor.
Step 6: Place 6 at the one’s place of the new divisor, resulting in 206. The obtained answer is 64, and we bring down 00.
Step 7: Continue the process of multiplying the current quotient by 2 to determine the next digit of the divisor, and repeat the division until reaching the desired level of accuracy.
Is 113 Perfect Square root or Not?
A perfect square is a number that can be expressed as the product of an integer with itself e.g.1, 4, 9, 16… Since there is no integer (n) such that (n × n = 113). 113 is not a perfect square.
FAQs
What is 113 divisible by?
113 is a prime number, which means it is only divisible by 1 and itself. Therefore, 113 is divisible by 1 and 113.
What are the factors of 113?
The factors of 113 are the numbers that divide 113 exactly without leaving a remainder. Since 113 is a prime number, its only factors are 1 and 113.
Share :
