Square & Square Root of 12
Square of 12
The square of 12, represented as 12, is calculated by multiplying 12 by itself, resulting in 144. This is a fundamental arithmetic operation where 12 is both the multiplicand and multiplier, leading to its squared value, 144.
Square root of 12
Or
√12 = 3.464 up to three places of decimal.
The square root of 12, represented as √12, falls into the category of irrational numbers, meaning it cannot be precisely expressed as a fraction. The approximate numerical value of √12 is 3.4641, situating it between the whole numbers 3 and 4. The fact that 12 is not a perfect square (a number that is an integer’s square) underlines why its square root, √12 does not simplify to an exact whole number.
Exponential Form of 12: = (12)½ or (12)0.5
Radical Form of 12: √12 or 2√3
Is Square Root of 12 Rational or Irrational?
The square root of 12 irrational number
The square root of 12 is a mathematical concept that prompts an exploration into its rationality or irrationality. To determine whether the square root of 12 is rational or irrational, we must first understand these terms.
Rational Numbers:
Rational numbers are those that can be expressed as a quotient or fraction of two integers, where the denominator is not zero. In other words, they can be written in the form a/b, where a and b are integers and b≠0. Rational numbers include integers, fractions, terminating decimals, and repeating decimals.
Irrational Numbers:
Conversely, irrational numbers cannot be expressed as a simple fraction of two integers. They are non-repeating and non-terminating decimals. Examples of irrational numbers include the square root of non-perfect squares, such as 22, 33, and π.
Now, let’s apply this understanding to the square root of 12.
Square Root of 12:
To find the square root of 12, we need to determine a number that, when multiplied by itself, equals 12. We can approximate the square root of 12 to be approximately 3.464. However, this is just an approximation.
To delve deeper into whether the square root of 12 is rational or irrational, let’s consider its exact value.
Method to Find Value of Root 12
To find the value of √12 without directly calculating square roots, consider these alternative approaches:
1. Estimation
Estimate the value by recognizing it lies between two known values. Since 12 is between the squares of 3 and 4 (9 and 16, respectively), its square root must be between 3 and 4. Observing that 12 is closer to 9 suggests the square root is just above 3.
2. Long Division Method
This method, akin to traditional long division, allows you to approximate the value digit by digit. It involves a systematic process of guessing, subtracting, and bringing down digits, akin to standard division but tailored for finding square roots.
3. Newton-Raphson Method
This iterative numerical technique refines an initial guess to find better approximations. Starting with a guess near the expected value, apply the iterative formula to converge on a more accurate approximation.
4. Calculator Method
For a straightforward approach, use a calculator’s square root function. Inputting “12” and pressing the square root button will give you a precise approximation instantly.
5. Numerical Series or Sequences
Some advanced mathematical series or sequences converge to square roots based on their properties. By calculating the terms of such a series, you can approximate the square root value.
Each method offers a different pathway to approximation, from quick and practical to more detailed and insightful, catering to various needs and contexts.
Square Root of 12 by Long Division Method
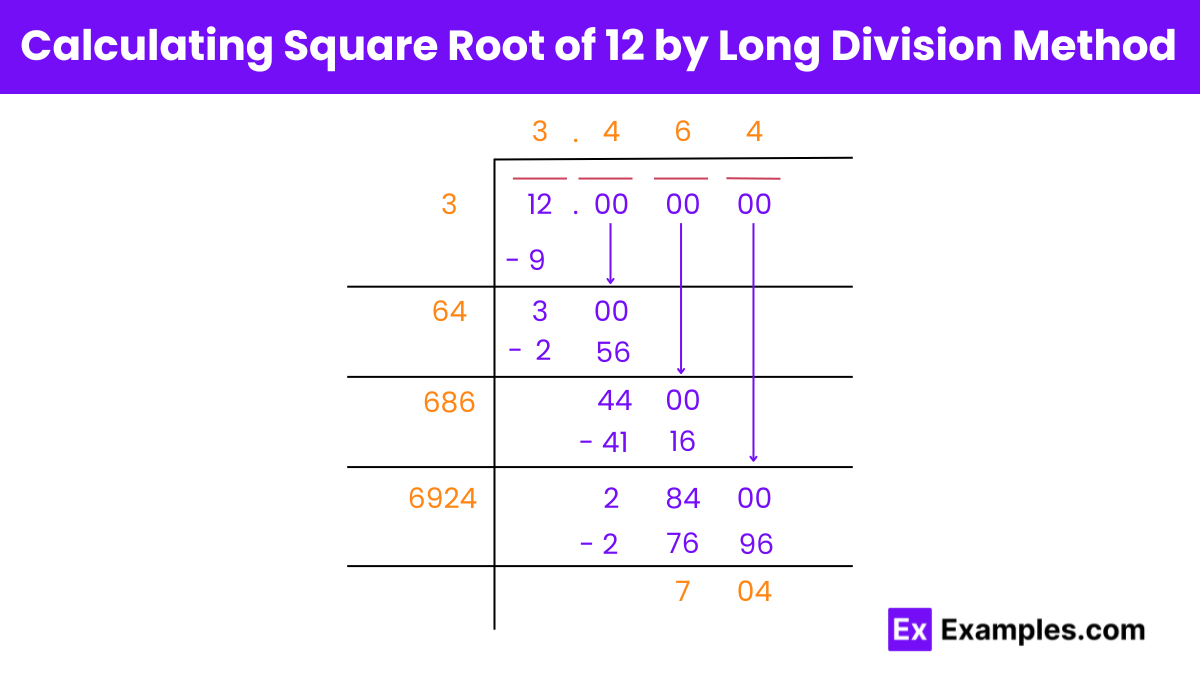
To find the square root of 12 using the long division method, we follow these steps:
- Start by separating the digits of 12 into pairs from the right. Since there are only two digits, we consider them together as one pair. So, we have 12.
- Now, we find the largest integer whose square is less than or equal to 12. In this case, the largest integer whose square is less than 12 is 3, because 3² = 9.
- Subtract the square of the number we found in step 2 from the first pair of digits (12 – 9 = 3).
- Bring down the next pair of digits to the right of the result obtained in step 3. Since there are no more digits, we can add a decimal point and a pair of zeros.
- Double the quotient obtained in step 2 and write it down as a temporary divisor. Add a digit to the quotient such that when we multiply the entire divisor by this new digit, the result is equal to or less than the dividend. In this case, the temporary divisor is 2 * 3 = 6, and the digit to add is 2. So, the new quotient is 3.2.
- Repeat steps 3 to 5 until we get the desired level of accuracy.
So, the square root of 12 by the long division method is approximately 3.4641016151377544.
FAQS
What is the simplified form of √12?
The simplified form of √12 involves factoring out the largest perfect square from 12, which is 4. This leaves you with 2√3, where 2 is the square root of 4, and √3 remains under the radical because 3 is a prime number.
What is equivalent to the square root of 12?
Equivalent to the square root of 12 is the expression 2√3. This is derived by factoring out the square root of the largest perfect square factor of 12, which is 4, leaving the square root of 3 as the remaining factor
What cubed root equals 12?
No perfect cube root equals 12. Cube roots are typically associated with numbers that are the product of a number multiplied by itself three times. For 12, there’s no whole number that, when cubed, equals 12.
Can you take the square root of 12?
Yes, you can take the square root of 12. It results in an irrational number, which cannot be precisely expressed as a fraction. The process involves either estimation, numerical methods, or factoring out the square root of a perfect square factor.
Is 12 a natural number?
Yes, 12 is a natural number. Natural numbers are the set of positive integers beginning from 1 and extending indefinitely. The number 12 falls into this category, being a whole, positive number.
In conclusion, the square of 12 is 144, and its square root is approximately 3.464. These mathematical values are fundamental in various disciplines, aiding in calculations and problem-solving. Understanding the relationship between squares and square roots enhances mathematical proficiency and facilitates applications in fields such as science, engineering, and finance.
Share :
