Square & Square Root of 13

Square of 13

13² (13×13) =169

The square of 13 is 169. In mathematical terms, when you multiply 13 by itself, the result is 169. This fundamental arithmetic operation is important in various contexts, including geometry, algebra, and physics. Understanding squares and their properties is foundational in mathematical reasoning and problem-solving.

Square Root of 13

√13= 3.60555128.

Or

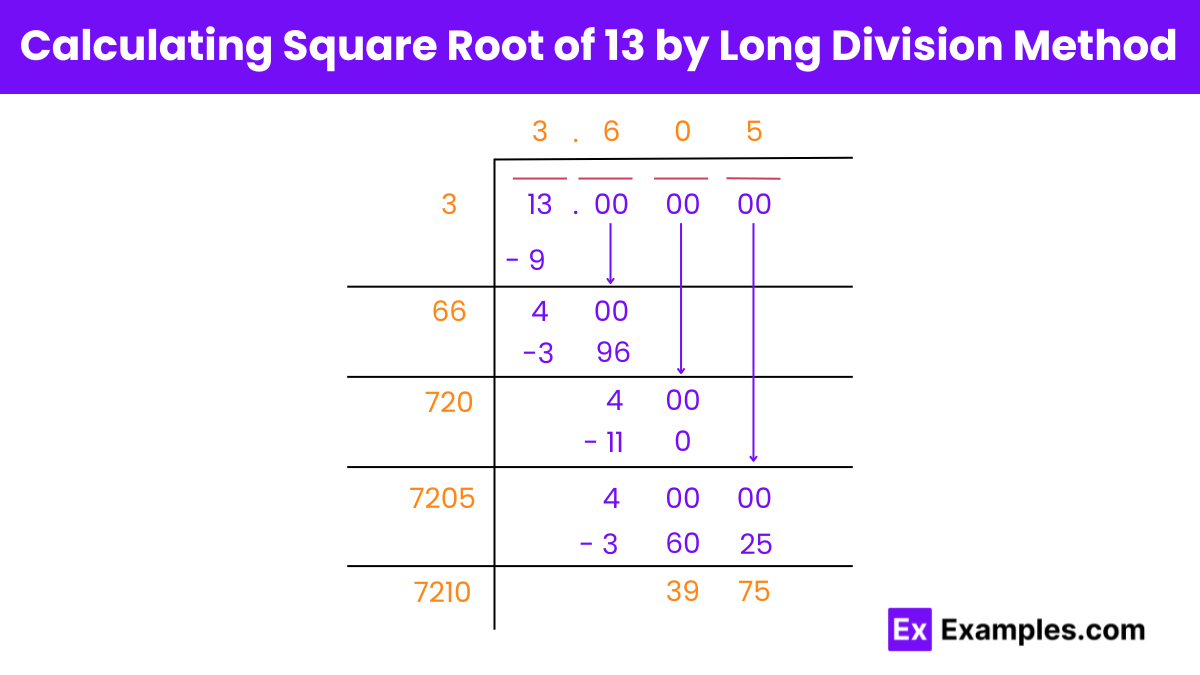
√13= 3.605 up to three places of decimal.

The square root of 13 is an irrational number, approximately equal to 3.60555. This means that when you multiply this number by itself, the result is 13. Finding the square root of 13 involves using methods such as long division or approximation techniques. In practical terms, the square root of 13 may be used in mathematical calculations, engineering, and other scientific applications.

Square Root of 13: 3.60555

Exponential Form of 13:= (13)^½ or (13)^0.5

Radical Form of 13: √13

Is the Square Root of 13 Rational or Irrational?

The square root of 13 is a irrational number.

Is the Square Root of 13 Rational or Irrational?

The square root of 13, denoted as √13, is an irrational number.

Explanation:

To determine whether the square root of 13 is rational or irrational, we need to understand the definitions of these terms.

• Rational Number: A rational number is a number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, it can be written in the form p/q​, where p and q are integers and q≠0.
• Irrational Number: An irrational number is a number that cannot be expressed as the quotient or fraction of two integers. It cannot be written in the form p/q​, where p and q are integers and q≠0. Additionally, irrational numbers cannot be expressed as terminating or repeating decimals.

When we calculate the square root of 13, we find that it cannot be expressed as a fraction of two integers. Furthermore, its decimal expansion does not terminate or repeat. Therefore, by definition, the square root of 13 is an irrational number.

Methods to Find Value of Root 13

There are several methods to find the value of the square root of 13:

1. Long Division Method: This method involves finding the square root of 13 through a series of divisions and iterations. While it can be time-consuming, it provides an accurate approximation of the square root.
2. Newton’s Method: Newton’s method is an iterative numerical technique used to approximate the roots of a real-valued function. It involves repeatedly applying a simple formula to refine the approximation until the desired level of accuracy is achieved.
3. Babylonian Method: Also known as Heron’s method, this iterative algorithm involves repeatedly averaging a guess with the original number divided by the guess. It converges quickly to the square root of a given number.
4. Using a Calculator or Computer: Most scientific calculators and computer software have built-in functions to calculate square roots accurately. Simply inputting the number 13 into such a device will provide its square root.
5. Tables or Reference Books: Older methods involved using pre-calculated tables or reference books that list the square roots of various numbers. While not as common nowadays, these resources can still be useful for educational purposes

Square Root of 13 by Long Division Method

1. Separate Digits: Write down “13” and separate the digits into pairs. Since there’s only one digit, consider it as a pair by itself.
2. First Approximation: Find the largest integer whose square is less than or equal to 13.
3. Subtract and Bring Down: Subtract the square of 3 from 13 to get 4. Bring down the next pair of digits (00) to the right of the result.
4. Double the Quotient: Double the quotient (3) obtained in the previous step and write it down as a temporary divisor (6). Add a digit to the quotient (3.x) such that when you multiply the entire divisor (6.x) by this new digit, the result is equal to or less than the dividend (400).
5. Trial and Error: Try different digits to add to the quotient to get as close to the dividend as possible without exceeding it.
6. Iterate: Repeat steps 3 to 5 until you reach the desired level of accuracy or until you’ve found the square root to the desired number of decimal places.
7. Check: Once you’ve found an approximation, square it to check if it’s close to 13. Adjust your approximation if necessary.
8. Finalize: Once you’re satisfied with your approximation, you can finalize the square root of 13 obtained through the long division method.

FAQS

Can √13 be simplified?

√13 cannot be simplified further into a simpler radical form because 13 is a prime number and has no perfect square factors other than 1. It remains as √13, representing an irrational number with a non-repeating, non-terminating decimal expansion.

Is 13 a perfect number?

No, 13 is not a perfect number. A perfect number is an integer that is the sum of its positive divisors, excluding itself. For example, 6 is a perfect number because 1 + 2 + 3 = 6.

Is 13 a squared number?

No, 13 is not a squared number. A squared number, or perfect square, is the product of an integer multiplied by itself. Since there’s no integer whose square is 13, it is not considered a squared number.

How to find square root?

To find a square root, you can use methods like estimation, the long division method, or a calculator. The long division method involves a step-by-step process similar to division, allowing you to find the square root to several decimal places.

What are the 13 perfect square numbers?

The first 13 perfect square numbers, starting from 1, are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and 169. These are the squares of the integers from 1 to 13, respectively.

In conclusion, the square of 13 is 169, a result of multiplying 13 by itself. On the other hand, the square root of 13, an irrational number, cannot be neatly expressed as a fraction, with an approximate value of 3.6055. These concepts underline the fascinating nature of numbers, bridging simple arithmetic and complex mathematical principles.