Square & Square Root of 14
Square of 14
The square of 14 is 196. In mathematical terms, when you multiply 14 by itself, the result is 196. Squaring a number involves multiplying it by itself, and in this case, the product is 196. Understanding squares and their properties is fundamental in various mathematical concepts and practical applications, such as geometry, algebra, and physics.
Square Root of 14
Or
√14 = 3.741 up to three places of decimal.
The square root of 14 is an irrational number, approximately equal to 3.74166. This means that when you multiply this number by itself, the result is 14. Finding the square root of 14 involves using mathematical methods such as long division or approximation techniques. In practical terms, the square root of 14 may be used in calculations involving areas, distances, or other measurements in various fields like engineering, science, and finance.
Exponential Form of 14: 14¹/² or 14⁰.⁵
Radical Form of 14: √14
Is the Square Root of 14 Rational or Irrational?
The square root of 14 is an irrational number.
To determine whether the square root of 14 is rational or irrational, we need to understand the definitions of these terms.
- Rational Number: A rational number is a number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, it can be written in the form p/q, where p and q are integers and q≠0
- Irrational Number: An irrational number is a number that cannot be expressed as the quotient or fraction of two integers. It cannot be written in the form p/q, where p and q are integers and q≠0. Additionally, irrational numbers cannot be expressed as terminating or repeating decimals.
When we calculate the square root of 14, we find that it cannot be expressed as a fraction of two integers. Furthermore, its decimal expansion continues indefinitely without repeating. Therefore, by definition, the square root of 14 is an irrational number.
Methods to Find Value of Root 14
There are several methods to find the value of the square root of 14:
- Long Division Method: This traditional method involves dividing the number into pairs of digits and finding the square root through a series of divisions and iterations.
- Newton’s Method: This iterative numerical technique uses calculus to approximate the roots of a real-valued function. It involves repeatedly applying a formula to refine the approximation until the desired level of accuracy is reached.
- Babylonian Method: Also known as Heron’s method, this iterative algorithm involves repeatedly averaging a guess with the original number divided by the guess. It converges quickly to the square root of a given number.
- Using a Calculator or Computer: Most scientific calculators and computer software have built-in functions to calculate square roots accurately. Simply inputting the number 14 into such a device will provide its square root.
- Tables or Reference Books: Older methods involved using pre-calculated tables or reference books that list the square roots of various numbers. While less common today, these resources can still be useful for educational purposes.
Square Root of 14 by Long Division Method
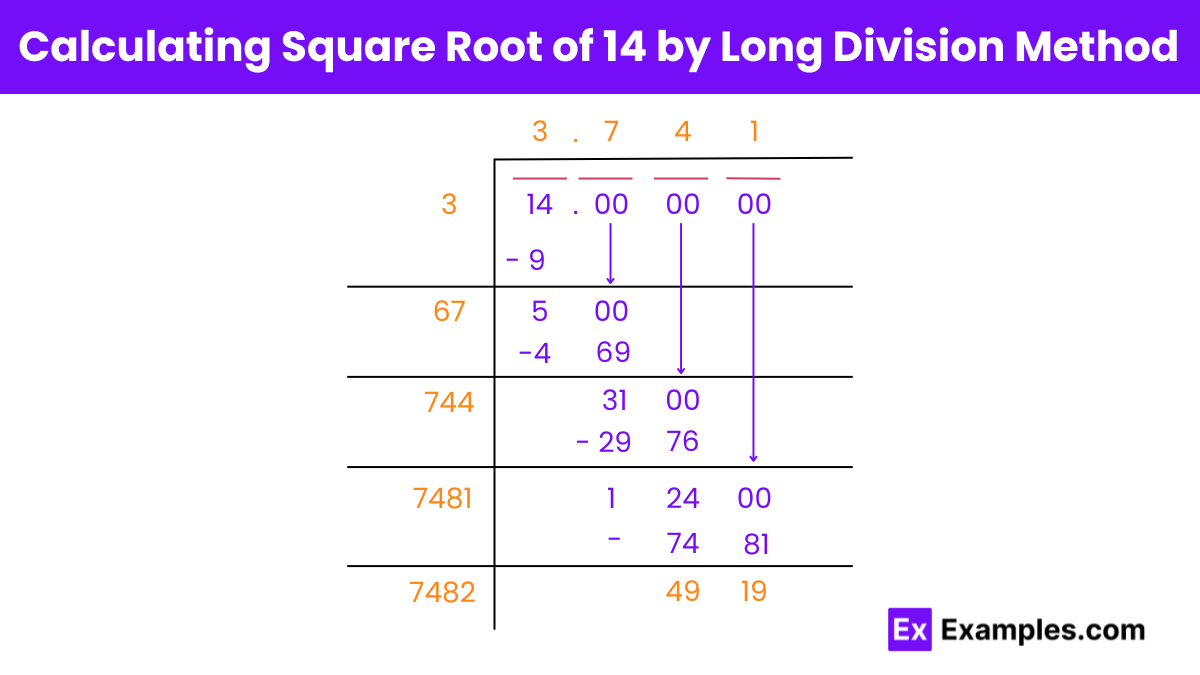
To find the square root of 14 using the long division method, follow these steps:
- Separate Digits: Write down “14” and separate the digits into pairs. Since there’s only one digit, consider it as a pair by itself.
- First Approximation: Find the largest integer whose square is less than or equal to 14. In this case, it’s 3 because 32=932=9.
- Subtract and Bring Down: Subtract the square of 3 from 14 to get 5. Bring down the next pair of digits (00) to the right of the result.
- Double the Quotient: Double the quotient (3) obtained in the previous step and write it down as a temporary divisor (6). Add a digit to the quotient (3.x) such that when you multiply the entire divisor (6.x) by this new digit, the result is equal to or less than the dividend (500).
- Trial and Error: Try different digits to add to the quotient to get as close to the dividend as possible without exceeding it.
- Iterate: Repeat steps 3 to 5 until you reach the desired level of accuracy or until you’ve found the square root to the desired number of decimal places.
- Check: Once you’ve found an approximation, square it to check if it’s close to 14. Adjust your approximation if necessary.
- Finalize: Once you’re satisfied with your approximation, you can finalize the square root of 14 obtained through the long division method.
FAQS
What is √14 rounded to the nearest whole number?
The square root of 14, when rounded to the nearest whole number, is approximately 4. This is because the actual value of √14 is about 3.74, which is closer to 4 than to 3 when rounded.
Is 14 squared a perfect square?
Yes, 14 squared, which equals 196, is a perfect square. A perfect square is the product of an integer with itself, and since 196 is the result of 14 multiplied by 14, it qualifies as a perfect square.
Is the cube root of 14 irrational?
The cube root of 14 is considered irrational. It cannot be expressed as a simple fraction because there’s no integer whose cube is exactly 14. Its decimal form is non-repeating and non-terminating, which are characteristics of irrational numbers.
Why is 14 the perfect number?
14 is not considered a perfect number in mathematics. A perfect number is defined as an integer that is the sum of its proper positive divisors, excluding itself, and 14 does not meet this criterion.
Is 14 a perfect square, yes or no?
No, 14 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer, and there’s no integer whose square is 14.
In conclusion, The square of 14 is 196, while the square root of 14 is approximately 3.74166. Understanding these numerical relationships is essential in various fields like mathematics, physics, and engineering. Squaring a number involves multiplying it by itself, while finding the square root involves determining the number that, when multiplied by itself, equals the given number.
Share :
