Square & Square Root of 15

Square of 15

15² (15×15) =225

The square of 15 is 225. When you multiply 15 by itself, the result is 225. This fundamental arithmetic operation is significant in various mathematical concepts and practical applications, such as calculating areas, volumes, and distances in geometry and engineering. Understanding squares and their properties is essential in mathematical reasoning and problem-solving.

Square Root of 15

√15 = 3.872983

Or

√15 = 3.872 up to three places of decimal.

The square root of 15 is an irrational number, approximately equal to 3.87298. It represents the number that, when multiplied by itself, equals 15. Finding the square root of 15 involves using mathematical methods such as long division or approximation techniques. In practical terms, it is used in calculations involving areas, distances, or other measurements in various fields like engineering, science, and finance.

Square Root of 15: 5

Exponential Form of 15: (15)^½ or (15)^0.5 

Radical Form of 15: √15

Is the Square Root of 15 Rational or Irrational?

To determine whether the square root of 15 is rational or irrational, let’s examine the definitions of these terms.

• Rational Number: A rational number is a number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In other words, it can be written in the form p/q​, where p and q are integers and q≠0.
• Irrational Number: An irrational number is a number that cannot be expressed as the quotient or fraction of two integers. It cannot be written in the form p/q​, where p and q are integers and q≠0. Additionally, irrational numbers cannot be expressed as terminating or repeating decimals.

Now, let’s consider the square root of 15. If we calculate it, we find that the square root of 15 is approximately 3.87298. This decimal representation neither terminates nor repeats, indicating that it is non-repeating and non-terminating.

Since the square root of 15 cannot be expressed as a fraction of two integers and its decimal expansion is non-repeating and non-terminating, we conclude that the square root of 15 is an irrational number.

Methods to Find Value of Root 15

Finding the square root of 15 involves various methods, each with its own unique approach and advantages. Here are six methods:

1. Long Division Method: A traditional approach where 15 is divided into pairs of digits, and the square root is determined through a series of divisions and iterations.
2. Newton’s Method: An iterative numerical technique that uses calculus to approximate the roots of a function, refining the approximation until desired accuracy is achieved.
3. Babylonian Method: Also known as Heron’s method, this iterative algorithm repeatedly averages a guess with the original number divided by the guess to converge quickly to the square root of 15.
4. Prime Factorization: Decomposing 15 into its prime factors (3 and 5) and using properties of exponents to simplify the square root expression.
5. Using a Calculator or Computer: Modern tools with built-in functions to accurately calculate square roots, providing quick and precise results.

Square Root of 15 by Long Division Method

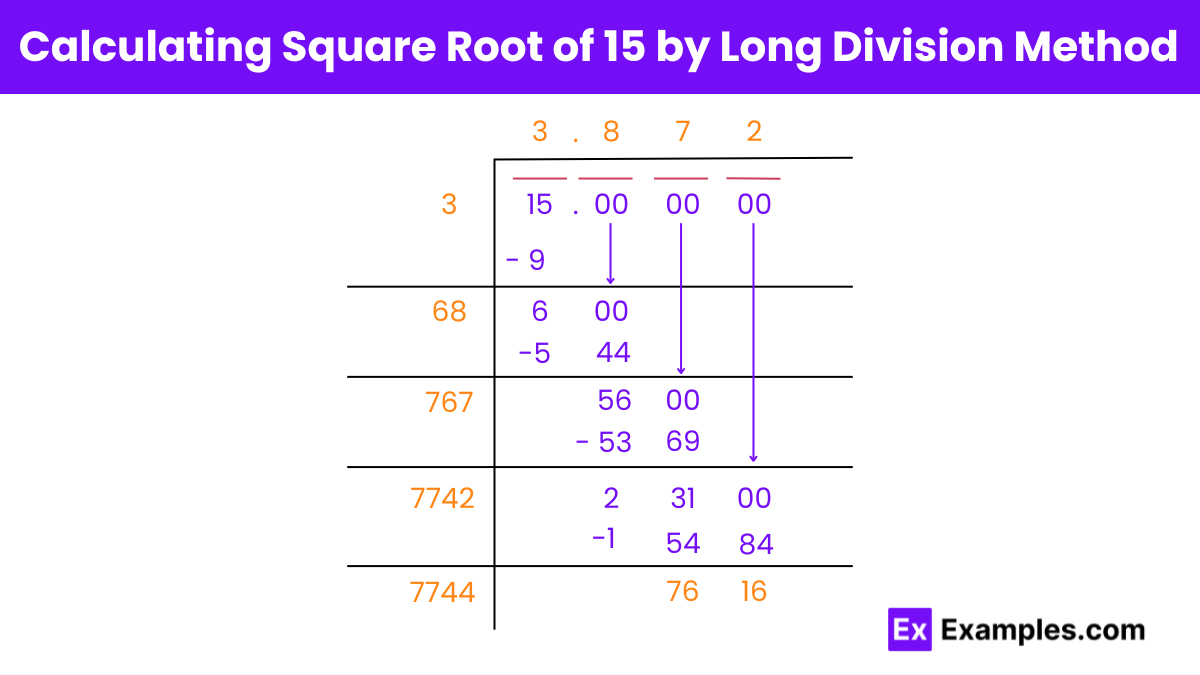
The long division method is a technique used to find the square root of a number by repeatedly subtracting perfect squares. In the case of finding the square root of 15, this method involves a step-by-step process of division and subtraction to approximate the square root.

Steps to Find the Square Root of 15 by Long Division:

1. Group Digits: Group the digits of 15 into pairs from the decimal point (15).
2. Starting Digit: Start with the largest digit that, when squared, is less than or equal to 15. In this case, it’s 3 (since 3^2 = 9).
3. Subtraction: Subtract 9 from 15, leaving 6.
4. Bring Down: Bring down the next pair of zeros to the right of 6, making it 600.
5. Divisor: Double the quotient (3) to get 6 and write it as the divisor with a blank space for a placeholder.
6. Next Digit: Find the largest digit that, when added to the divisor (6), produces a number less than or equal to 600. The digit is 2 (since (6+2)^2 = 64).
7. Subtraction: Write down 2 next to the divisor and subtract (6 + 2)^2 = 64 from 600, leaving a remainder of 536.
8. Repeat: Continue the process until the desired level of accuracy is reached.

By following these steps, the square root of 15, rounded to three decimal places, is approximately 3.873.

FAQS

What are the perfect squares up to 15 squared?

The perfect squares up to 15 squared are: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225.

Is the square root of 15 a whole number?

No, the square root of 15 is not a whole number. It is an irrational number, approximately equal to 3.87298.

Does 15 have a perfect square factor?

Yes, 15 has a perfect square factor, which is 3^2 (equal to 9).

Is 15 a perfect cube or square?

No, 15 is neither a perfect cube nor a perfect square. It cannot be expressed as the cube or square of an integer.

Is the negative square root of 15 a real number?

Yes, the negative square root of 15 is a real number. It is approximately equal to -3.87298.

In conclusion, the square of 15 is 225, while the square root of 15 is approximately 3.87298. Understanding these numerical relationships is crucial in various fields such as mathematics, engineering, and physics. Squaring a number involves multiplying it by itself, while finding the square root entails determining the number that, when multiplied by itself, equals the given number.