Square & Square Root of 17

Square of 17

17² (17×17) = 289

The square of 17, denoted as 17^2, is the result of multiplying the number 17 by itself. In simpler terms, it’s the area of a square with side length 17 units. This mathematical operation yields the value 289. Understanding the square of 17 is fundamental in arithmetic and geometry.

Square root of 17

√17​ = 4.123105625617661

or

√17​=4.123 up to three places of decimal

The square root of 17, symbolized as √17, is a fundamental concept in mathematics. It represents the value that, when multiplied by itself, results in 17. In simpler terms, it’s the number which, when squared, equals 17. However, unlike whole numbers or fractions, the square root of 17 is an irrational number. This means its decimal representation goes on infinitely without repeating a pattern. When calculated, the approximate value of the square root of 17 is 4.123105625617661. Despite its seemingly random decimal expansion, the square root of 17 holds significance in various mathematical calculations, geometric problems, and real-world applications. Understanding this concept helps us comprehend the relationship between numbers, shapes, and quantities, contributing to problem-solving and analytical skills in fields such as engineering, physics, and finance.

Square Root of 17:4.123105625617661

Exponential Form:17^½ or 17^0.5

Radical Form:√17

Is the Square Root of 17 Rational or Irrational?

The square root of 17 is an irrational number.

To understand why, let’s delve into the definitions of rational and irrational numbers.

• Rational numbers are those that can be expressed as a fraction of two integers, where the denominator is not zero. In other words, they can be written in the form a/b, where a and b are integers and b is not equal to zero.

Examples of rational numbers include 1/2, -3, and 5.

• An irrational numbers cannot be expressed as a simple fraction of two integers. Their decimal representations are non-repeating and non-terminating.

Examples of irrational numbers include √2, π (pi), and √3.

Square Root of 17 as Irrational:

• When we calculate the square root of 17, we find that it cannot be expressed as a fraction of two integers.
• Its decimal expansion, approximately 4.123105625617661, goes on infinitely without repeating a pattern.

To understand why the square root of 17 is irrational, let’s simplify it:

√17 = √(16 + 1) = √16 * √1 = 4 * √1 = 4

Now, we know that 4 is a rational number. However, √1 is famously rational. It cannot be represented as a fraction of two integers, and its decimal form goes on forever without repeating. Therefore, 4 is also irrational because the product of a rational number (4) and an irrational number (√1) is always irrational.

In summary, the square root of 17 is irrational because it simplifies to a rational number (4), and when combined with the irrational √1, the result is always irrational.

Method to Find Value of Root 17

To find the square root of 17, we can utilize various methods, including estimation, prime factorization, and using a calculator. Here’s a breakdown of a simple estimation method:

1. Identify Perfect Squares Around 17: Recognize that the perfect square closest to but less than 17 is 16 (4²=16), and the perfect square closest to but more than 17 is 25 (5²=25).
2. Estimation: Since 17 is between 16 and 25, its square root will be between 4 and 5.
3. Refinement: For a more precise value, use a calculator or a square root table. The square root of 17 is approximately 4.123105625617661.
4. Simplified Radical Form: The square root of 17 can also be expressed in simplified radical form as √17=√16×1=4√1.

Square Root of 17 by Long Division Method

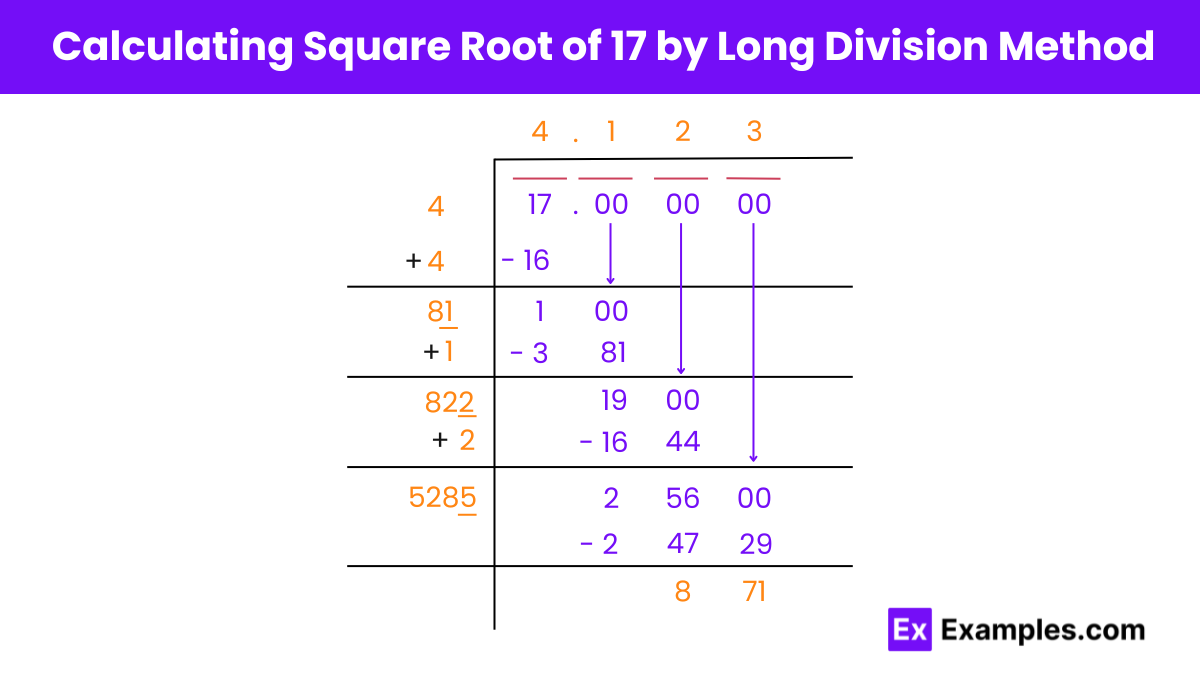
Finding the square root of 17 using the long division method involves the following steps:

Step 1: Preparation

Write 17 as 17.00 00 00, grouping digits in pairs from the decimal point. For 17, it looks like “17”.

Step 2: Find the Largest Square

Identify the largest square smaller than or equal to 17, which is 16 (4²). Place 4 above the line as the first digit of the root.

Step 3: Subtract and Bring Down

Subtract 16 from 17 to get 1, then bring down the next pair of zeros to make it 100.

Step 4: Double and Find the Next Digit

Double the current result (4) to get 8. Now, find a digit (X) such that 48 multiplied by X is less than or equal to 100. Here, X is 2, because 482×2=96.

Step 5: Repeat with Precision

Subtract 96 from 100 to get 4, bring down the next zeros to get 400, then double the quotient (42) to get 84. Choose a digit (Y) so that 84Y multiplied by Y is just under 400.

Step 6: Finish at Desired Accuracy

Continue the process until reaching the desired level of accuracy. For the square root of 17, this method gives us about 4.123 as we extend the division

17 is Perfect Square root or Not

17 Is Not a Perfect Square Root

A perfect square root is a number that can be expressed as the product of an integer multiplied by itself. For example, 4 (2 × 2) and 9 (3 × 3) are perfect square roots.

However, when we examine 17, we find that it cannot be expressed as the product of two identical integers. There are no integers x such that x × x equals 17.

Therefore, 17 is not a perfect square root. It doesn’t have an integer square root. While it does have a square root (√17), it’s an irrational number and not the result of multiplying any whole number by itself.

FAQ’s

Is √17 a real number?

Yes, the square root of 17, denoted as √17, is a real number. A real number is any number that can be found on the number line, including both rational and irrational numbers. Since √17 exists on the number line and is not an imaginary number (which involve the square root of negative numbers), it is classified as a real number.

Is 17 an integer yes or no?

Yes, 17 is an integer. An integer is a whole number that can be positive, negative, or zero. Since 17 is a whole number and not a fraction or a decimal, it falls under the category of integers.