square & square root of 1764 – Examples, Methods, Calculation

In the realm of mathematics, specifically within algebraic studies, the foundational concepts of squares and square roots hold paramount importance. The process of squaring a number, exemplified by taking a number like 1764 and multiplying it by itself to yield a result of 3111696, is a fundamental operation. This operation serves as a cornerstone in investigating the properties inherent in both rational numbers (those expressible as a fraction of two integers) and irrational numbers (which defy expression as a neat fraction). A comprehension of these fundamental concepts serves to enrich one’s understanding of mathematical relationships and patterns.

Square of 1764

The square number of 1764, a fundamental operation in mathematics, yields 3,111,696. This process involves multiplying the number by itself, showcasing the significance of squaring in algebraic exploration. It elucidates properties of both rational and irrational numbers, enhancing comprehension of mathematical patterns and relationships.

Square Root of 1764

The square root of 1764, an essential concept in mathematics, is 42. This value represents the number that, when multiplied by itself, equals 1764. Understanding square roots is vital for grasping algebraic relationships and exploring the properties of numbers, both rational and irrational. It elucidates fundamental mathematical principles and aids in solving various problems across different domains.

Is the Square Root of 1764 Rational or Irrational?

The square root of 1764, which is 42, is a rational number. A rational number is one that can be expressed as a fraction of two integers, and since 42 can be represented as 42/1, it fits this definition. Unlike irrational numbers, rational numbers terminate or repeat in decimal form, making them distinct within the realm of mathematics.

A rational number is any number expressible as a fraction of two integers.
Examples : 3/4 or -5/2

An irrational number cannot be expressed as a fraction of two integers and its decimal expansion neither terminates nor repeats.
Examples : √2, which is approximately 1.41421356…, is irrational.

Methods to Find Value of Root 1764

There are several methods to find the square root of 1764:

1. Prime Factorization Method: Express 1764 as a product of its prime factors (2² × 3² × 7²) and then take the square root of each prime factor. The result is 2 × 3 × 7 = 42.
2. Estimation Method: Approximate the square root of 1764 by considering perfect squares near it. Since 42² = 1764, the square root of 1764 is 42.
3. Long Division Method: Use long division to find the square root iteratively. Start by guessing a number (e.g., 40) and then refine the guess through division and averaging until reaching the accurate value.
4. Calculator: Utilize a calculator with a square root function to directly find the square root of 1764. Simply input 1764 and find its square root, which is 42.

Square Root of 1764 by Long Division Method

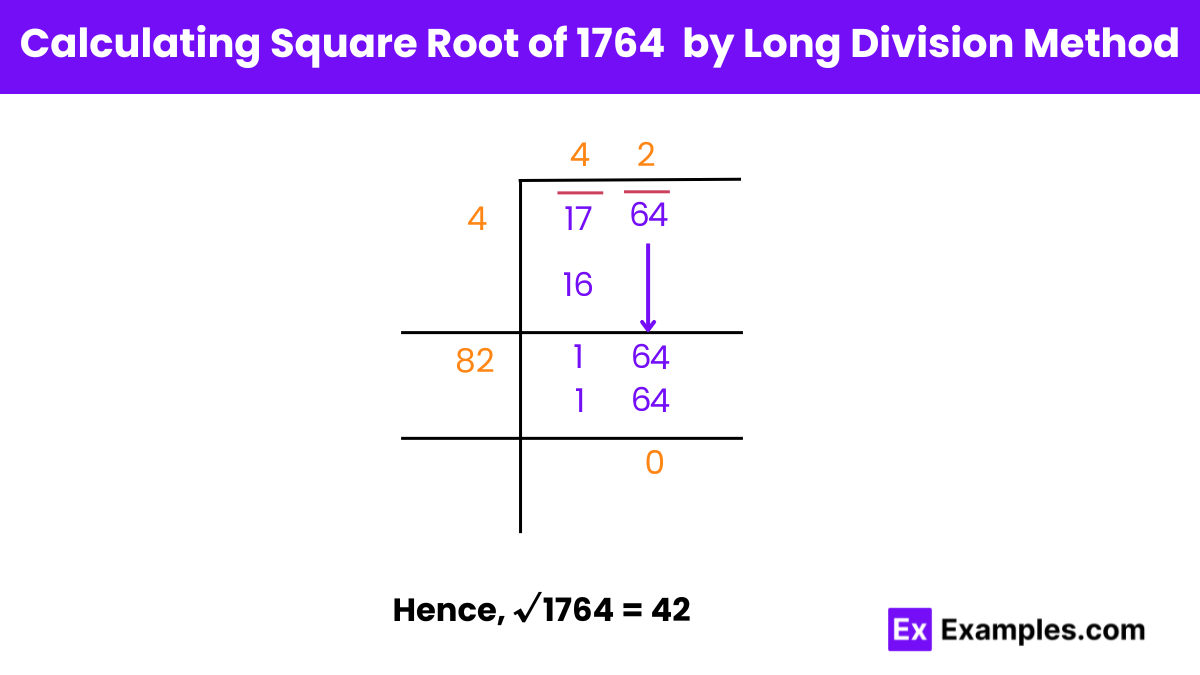
Forming Pairs: 17 and 64 We start by forming pairs from the number 1764. The pairs formed are 17 and 64.

Finding the Initial Digit Y (4) To find the initial digit Y such that its square is less than or equal to 17, we determine that Y = 4.

Initial Division: 17 divided by Y (4) We divide 17 by 4, which gives us a quotient of 4.

New Dividend: 164 After dividing, we bring down the next pair, 64, to the right of the remainder 1, forming the new dividend 164.

Finding Digit Z (2) To find the next digit Z such that the product of (8Z) and Z is less than or equal to 164, we determine that Z = 2.

New Divisor: 82 We combine the last digit of the quotient (4) with the newly found digit Z (2) to form the new divisor 82.

Further Division: 164 divided by 82 We divide 164 by the new divisor 82, resulting in a quotient of 2 and a remainder of 0.

Stopping the Process Since the remainder is now 0 and there are no more digits to bring down, we conclude the long division process.

Final Result: Square Root of 1764 Thus, the square root of 1764, found by the long division method, is 42.

1764 is Perfect Square root or Not

Yes, 1764 is a perfect square. Its square root is 42. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In this case, 42 × 42 equals 1764, confirming that 1764 is indeed a perfect square.

FAQs

What is the simplest form of 1764?

The factors of 1764 are 2 × 2 × 3 × 3 × 7 × 7. Simplifying these factors yields 42, making the correct option (d) “42”.

What is the HCF of 1764?

The highest common factor (HCF) of 1764 is 42. This is because 1764 can be expressed as the product of its prime factors, and 42 is the greatest common factor among them.

What number squared equals 1764?

The number squared to equal 1764 is 42. In mathematical terms, (42² = 1764).