Square & Square Root of 1849 – Methods, Calculation, How to find

In the realm of mathematics, algebra’s core principles encompass squares and square roots. This process underpins exploration of properties intrinsic to rational (expressible as fractions) and irrational numbers. Understanding these notions enriches comprehension of mathematical relationships, fostering deeper understanding within algebraic studies, and uncovering intricate connections shaping numerical and algebraic reasoning.

Square of 1849

A square number results from multiplying an integer by itself. The square of 1849 is 3,420,601. In mathematics, square numbers exhibit distinct properties, crucial for understanding algebraic relationships and patterns. Exploring the square of 1849 unveils fundamental principles, enriching comprehension of mathematical structures and operations.

Square Root of 1849

The square root, a fundamental concept in mathematics, reveals the number that, when multiplied by itself, yields the original number. The square root of 1849 is approximately 43. Understanding square roots elucidates the properties and relationships underlying numbers, offering insights into the square of 1849 and its mathematical significance.

Is the Square Root of 1849 Rational or Irrational?

This is because 1849 is a perfect square, specifically 43², and therefore its square root is an integer, making it a rational number.

An irrational number is a real number that cannot be expressed as a fraction of two integers and whose decimal representation is non-repeating and non-terminating.

Methods to Find Value of Root 1849

Prime Factorization Method:

Factorize 1849 as (43 × 43).

The square root is (43).

Estimation Method:

Find the two perfect squares around 1849: (42² = 1764) and (43² = 1849).

Since 1849 is closer to (43²), the square root is approximately (43).

Babylonian Method (Iterative):

Start with an initial guess, say (x_0 = 20).

Use the iteration formula (xₙ₊₁ = 1/2(xₙ + 1849/xₙ).

Continue iterating until the result stabilizes around 43.

Using a Calculator:

• Input √1849 into a calculator to get the exact value, which is (43).

Long Division Method:

Perform long division to manually find the square root, similar to how you’d divide numbers manually.

This method can be time-consuming but helps understand the concept better.

Square Root of 1849 by Long Division Method

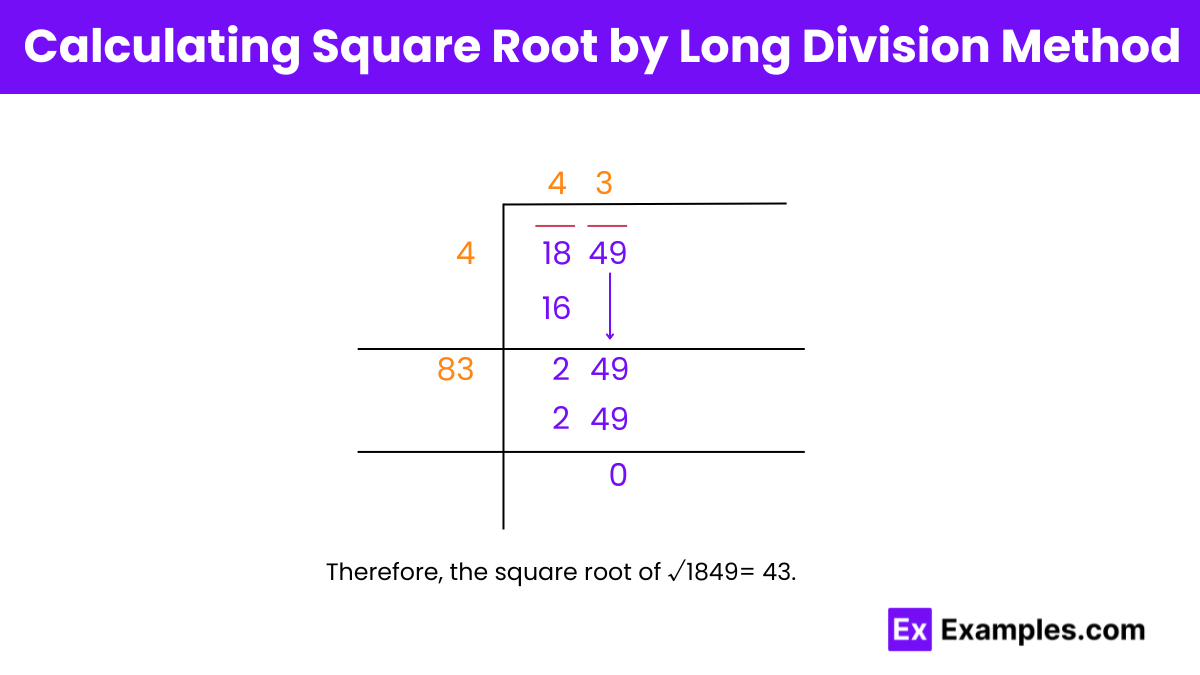
Step 1: Find a number Y (4) such that its square is less than or equal to 18. Now divide 18 by 4 with the quotient as 4.

Step 2: Bring down the next pair, 49, to the right of the remainder 2. The new dividend is now 249.

Step 3: Add the last digit of the quotient (4) to the divisor (4), i.e., 4 + 4 = 8. To the right of 8, find a digit Z (which is 3) such that (8Z × Z ≤ 249). After finding Z, together 8 and Z (3) form a new divisor 83 for the new dividend 249.

Step 4: Divide 249 by 83 with the quotient as 3, giving the remainder = (249 – 83 × 3 = 249 – 249 = 0).

Is 1849 Perfect Square root or Not

It is the square of the integer 43, because (43 × 43 = 1849).

FAQ’S

What is the factorization of 1849?

The factorization of 1849 is (43 × 43), where both factors are prime numbers.

What are the multiples of 1849?

The multiples of 1849 are obtained by multiplying 1849 by integers. Some multiples of 1849 include:

(1849×1 = 1849)

(1849×2 = 3698)

(1849×3 = 5547)

(1849×4 = 7396)

(1849×5 = 9245)

And so on…