Square & Square Root of 200
Square of 200
The square of 200 is 200×200 = 40,000. This means that when you multiply 200 by itself, the result is 40,000.
The square of a number is found by multiplying the number by itself. In the case of 200, you multiply 200 by 200. This multiplication results in 40,000, which is termed as the square of 200.
Square Root of 200
The square root of 200 is approximately 14.1421. This is the number that, when multiplied by itself, gives the product 200. The square root can be calculated more precisely with tools such as calculators or specialized software.
Square Root of 200 : 14.1421
Exponential Form : 200^½ or 200^0.5
Radical Form : √200
Is the Square Root of 200 Rational or Irrational?
The square root of 200 is irrational. An irrational number is a number that cannot be exactly expressed as a simple fraction, meaning its decimal form is non-terminating and non-repeating. Since 200 is not a perfect square, its square root does not result in a whole number or a simple fraction, leading to an irrational number approximately equal to 14.1421.
Method to Find Value of Root 200
Estimation Method
- Initial Guess: Start with a number that when squared is close to 200. Since 142 = 196 and 152 = 225, we know that the square root of 200 is between 14 and 15.
- Refinement using Averaging: Make an initial guess. Let’s use 14 since 142 = 196 is very close to 200.
- Compute the next guess using the formula: next guess = (current guess+200/current guess)/2
- Substitute the initial guess: next guess = (14+200/14)/2 = 14.142857.
- Iterate if Necessary:Repeat the averaging step with the new guess until the value changes insignificantly between iterations.
- A second iteration would look like this: next guess = (14.142857+200/14.142857)/2 = 14.142136
- Result:After a few iterations, you will notice that the result stabilizes around 14.1421, which is a close approximation of 200.
Square Root of 200 by Long Division Method
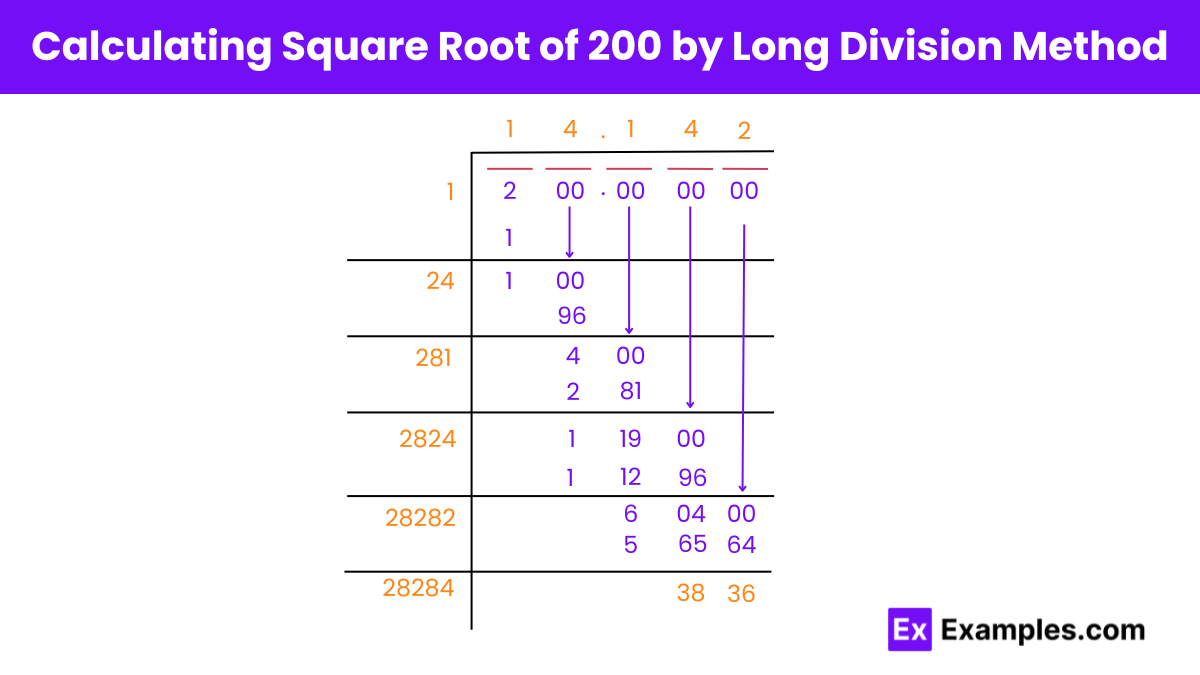
Step 1: Setup
- Write the number as 200.000000 and pair the digits from the right: [2][00][00][00]. The first group is 2.
- Find the largest integer whose square is less than or equal to 2. The integer 1 fits because 12=1.
Step 2: First Division
- Place 1 as the quotient. Subtract 12 from 2, leaving a remainder of 1. Bring down the next pair of zeros, making the dividend now 100.
Step 3: Update Divisor
- Double the quotient (now 1) to get 2 and append a digit to form a new divisor (20X). Find X such that 20X×X is as close to 100 as possible without exceeding it.
Step 4: Second Digit
- 24×4=96 is close to 100. Place 4 in the quotient next to 1, making it 14. Subtract 96 from 100, giving a remainder of 4. Bring down the next pair of zeros, resulting in a new dividend of 400.
Step 5: Third Division
- Double the current quotient (14) to get 28. Form a new divisor as 280X, and find X such that 280X×X is as close to 400 as possible.
- 281×1=281 fits well. Place 1 in the quotient, making it 141. Subtract 281 from 400, leaving a remainder of 119. Bring down the next pair of zeros to form a new dividend of 11900.
Step 6: Continue the Process
- Double the current quotient (141) to get 282. Use 282X to find X such that 282X×X fits into 11900.
- Continue this process iteratively, refining the quotient until the division stabilizes or reaches the desired number of decimal places.
Step 7: Result
- The process results in a quotient of approximately 14.142, which is a close approximation of the square root of 200.
200 is Perfect Square root or Not?
No, 200 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since there is no whole number that, when multiplied by itself, equals 200, it cannot be considered a perfect square. For instance, the squares of the numbers immediately surrounding the square root of 200 are 142=196 and 152=225, both of which do not equal 200. Thus, 200 lacks a whole number square root and is not a perfect square.
FAQs
Why is it important to know if a number is a perfect square in mathematics?
Knowing if a number is a perfect square is important for simplifying radical expressions, solving quadratic equations, and understanding properties of geometric figures.
Are there real-world applications for knowing the square root of a number like 200?
Yes, the square root is useful in various fields such as engineering, architecture, and physics, where calculations involving areas and resistances (in case of square laws) are necessary.
Share :
