Square & Square Root of 289
Square & Square Root of 289
Square of 289
The square of 289 is 83,521
289×289 = 83,521.
So, the square of 289 is 83,521. This means that if you take the number 289 and multiply it by itself, you will get 83,521 as the result.
This calculation is often used in various mathematical problems, such as finding areas of squares or rectangles with sides of length 289 units, or in algebraic expressions involving squares of numbers.
Square Root of 289
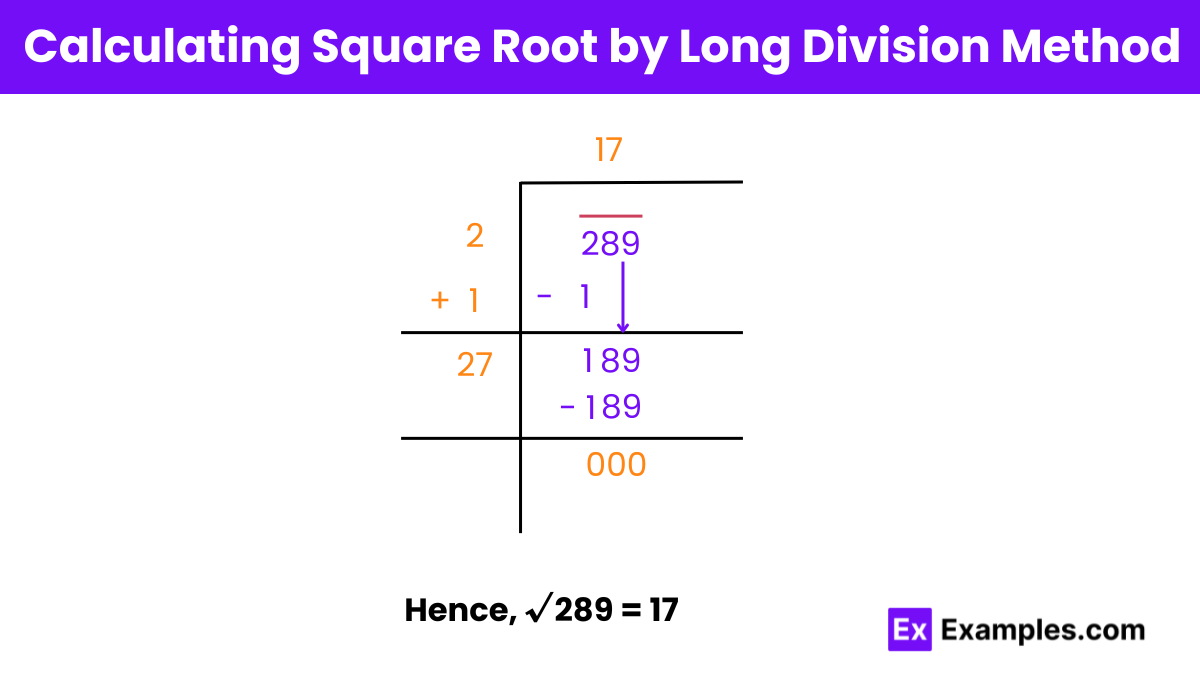
The square root of 289 is 17.
The square root of a number is a value that, when multiplied by itself, gives the original number. For 289, we are looking for a number x such that x×x = 289. After performing the calculation or using a calculator, we find that 17×17 = 289. Therefore, 17 is the square root of 289. This is a straightforward example of a perfect square, where the root is an integer.
Exponential Form : 289^½ or 289^0.5
Radical Form : √289
Is the Square Root of 289 Rational or Irrational?
The square root of 289 is rational. A rational number is defined as one that can be expressed as the fraction of two integers (a ratio), where the denominator is not zero. Since the square root of 289 is exactly 17, and 17 can be written as 17/1, it is a rational number.
Method to Find Value of Root 289
Prime Factorization: Begin by factorizing 289 into prime factors. You continue dividing by the smallest prime (which, in this case, is itself since 289 is a prime number) until all factors are prime.
289 = 17×17
Square Root: Since the square root of a product of prime factors is the product of the square roots of each factor, and each factor is the same (17), the square root of 289 is simply 17.
This method confirms that 289 = 17. You can also use this method with calculators or computational tools for larger numbers where manual factorization would be impractical.
Square Root of 289 by Long Division Method
- Step1 : Start by grouping the digits of the number (289) into pairs from the right. Since 289 has three digits, the grouping will be 2×89.
- Step2 : Identify the largest square less than or equal to the first group, which is 2. The largest perfect square is 1 (since 12=1). Subtract this from 2, leaving a remainder of 1.
- Step3 : Bring down the next pair, making the number now 189 (appending 89 to the remainder 1).
- Step4 : The initial divisor is the square root of the first perfect square found (1 in this case) doubled. So, 1+1=2. Place this beside the remainder with a space on the right for the new digit.
- Step5 : Find a digit (let’s say X) which when added to the end of the new divisor (2X) and also placed as the next digit, maximizes the product 2X×X without exceeding 189. For 289, this digit is 7, as 27×7=189
- Step6 : Since the remainder is now 0, we conclude that the square root of 289 is 17.
289 is Perfect Square root or Not?
Yes, 289 is a perfect square. A number is considered a perfect square if there is an integer that can be squared to produce the original number. In the case of 289, the integer 17 squared (17 x 17) equals 289, making it a perfect square.
FAQs
What are the methods to find the square root of 289?
- The square root of 289 can be found using several methods such as:
- Prime factorization
- Using a calculator
- Long division method
- Approximation method
What is the significance of 289 being a perfect square in mathematics?
The significance lies in its properties that simplify calculations in various mathematical fields, such as algebra, geometry, and number theory. It also helps in solving quadratic equations and understanding geometric concepts involving areas.
Are there any interesting patterns involving the square root of 289?
One interesting pattern is that both the square root of 289 (17) and the square itself (289) consist of digits 1 through 9 exactly once (1 and 9 in 289 and 1 and 7 in 17).
Share :
