Square & Square Roots
Square & Square Roots
What are Square and Square Roots?
Squares and square roots are fundamental mathematical operations. A square of a number is obtained by multiplying the number by itself, while the square root of a number is a value that, when multiplied by itself, gives the original number. These concepts are crucial in various fields, including algebra, geometry, and physics.
How to find Square Root?
Finding the square root of a number is to determine which number, when multiplied by itself, equals the original number. There are several methods to find square roots, each suitable for different kinds of numbers.
1. Finding Square Root Using Trial and Error Method
This method involves guessing the square root of a number and refining the guess based on its square.
- Step 1: Make an initial guess of what the square root might be.
- Step 2: Square your guess. If the result is too high or too low, adjust your guess accordingly.
- Step 3: Repeat the process until you find a number whose square exactly equals the original number.
To find √16, you might guess 4. Since 4² = 16, your guess is correct.
2. Square Root by Prime Factorization Method
Prime factorization involves breaking down a number into its prime factors and identifying pairs of identical factors.
- Step 1: Divide the original number into its prime factors.
- Step 2: Group the prime factors into pairs of identical numbers.
- Step 3: For each pair of identical factors, take one number out of the square root.
- Step 4: Multiply these numbers together to get the square root of the original number.
Formula: √(a² × b² × c² × …) = a × b × c × …
Examples: To find √144, note that 144 = 2² × 2² × 3². So, √144 = 2 × 2 × 3 = 12.
3. Repeated Subtraction Method of Square Root
- Step 1: Pick the number you want to find the square root of. Make sure it’s a perfect square.
- Step 2: Subtract odd numbers from your chosen number, starting with 1, then 3, then 5, and so on.
- Step 3: Count each subtraction you make. This number will be important for finding your answer.
- Step 4: Keep subtracting until you get down to zero. If the number is a perfect square, you’ll get to zero exactly.
- Step 5: The total number of subtractions you made is the square root of your original number.
Example: Square Root of 16
- 16 – 1 = 15
- 15 – 3 = 12
- 12 – 5 = 7
- 7 – 7 = 0
- Start with 16.
- Subtract odd numbers in order: 1, then 3, then 5, then 7.
- It takes 4 subtractions to get to zero.
- So, the square root of 16 is 4.
This method is easy to understand and shows how square roots work, especially useful for learning with smaller, perfect square numbers.
3. Calculating Square Root by Long Division Method
The long division method is a systematic approach suitable for finding the square roots of both perfect and non-perfect squares.
- Step 1: Place a bar over every pair of digits starting from the decimal point (or the unit’s place if there’s no decimal).
- Step 2: Find the largest number whose square is less than or equal to the first set of numbers under the leftmost bar. Place this number above the bar.
- Step 3: Subtract the square of the number you found from the number under the bar and bring down the next set of digits next to the remainder.
- Step 4: Double the number above the bar (the divisor) and find a new digit that, when added to the divisor and multiplied by the same digit, is less than or equal to the remainder. Add this digit to the top.
- Step 5: Repeat Steps 3 and 4 until all digits have been brought down.
Example: Finding √1225 involves dividing it into pairs (12 and 25), guessing the first digit of the root, subtracting its square, and continuing the process with what remains.
4. Finding Square Root Using a Calculator
For most practical purposes, calculators provide the quickest and most accurate square roots.
- Step 1: Enter the number whose square root you want to find into the calculator.
- Step 2: Press the square root button (√) to get the result instantly.
Example: Inputting 144 and pressing √ yields 12.
5. Finding Square Root by Estimation Method
Estimation is useful when an approximate square root is sufficient, especially if the number is not a perfect square.
- Step 1: Find the nearest perfect squares above and below the given number.
- Step 2: Estimate that the square root of your number lies between the square roots of these perfect squares.
- Step 3: Refine your estimate based on how close the number is to the lower or upper bounds.
Example: For √50, since 49 (7²) is below and 64 (8²) is above, estimate √50 to be between 7 and 8, closer to 7.
6. Calculation of Square Root by Graphical Method
This method uses the curve of the equation y = x² to find square roots graphically.
- Step 1: Plot the curve y = x² on graph paper.
- Step 2: Draw a horizontal line at y equals the number whose square root you’re finding.
- Step 3: The points where the horizontal line intersects the curve give the square roots of the number.
Example: To find √49, draw a horizontal line at y = 49 across the curve y = x². The points of intersection at x = 7 (and x = -7) give the square roots.
Square Root Table
| Number | Square Root | Number | Square Root | Number | Square Root |
|---|---|---|---|---|---|
| 1 | 1.000 | 18 | 4.243 | 35 | 5.916 |
| 2 | 1.414 | 19 | 4.359 | 36 | 6.000 |
| 3 | 1.732 | 20 | 4.472 | 37 | 6.083 |
| 4 | 2.000 | 21 | 4.583 | 38 | 6.164 |
| 5 | 2.236 | 22 | 4.690 | 39 | 6.245 |
| 6 | 2.449 | 23 | 4.796 | 40 | 6.325 |
| 7 | 2.646 | 24 | 4.899 | 41 | 6.403 |
| 8 | 2.828 | 25 | 5.000 | 42 | 6.481 |
| 9 | 3.000 | 26 | 5.099 | 43 | 6.557 |
| 10 | 3.162 | 27 | 5.196 | 44 | 6.633 |
| 11 | 3.317 | 28 | 5.292 | 45 | 6.708 |
| 12 | 3.464 | 29 | 5.385 | 46 | 6.782 |
| 13 | 3.606 | 30 | 5.477 | 47 | 6.856 |
| 14 | 3.742 | 31 | 5.568 | 48 | 6.928 |
| 15 | 3.873 | 32 | 5.657 | 49 | 7.000 |
| 16 | 4.000 | 33 | 5.745 | 50 | 7.071 |
| 17 | 4.123 | 34 | 5.831 |
Square Root Formula
The square root formula is used to find the square root of a number, which is the value that, when multiplied by itself, equals the original number. The formula is expressed as:
where:
- √x represents the square root of x,
- y is the value that, when squared (y²), equals x.
For example, if x=9, then √9=3 because 3²=9.
This formula is fundamental in mathematics for solving problems involving square roots, including equations and understanding geometric properties.
Properties of Square Root
- Product Rule: The square root of two numbers multiplied together is the same as multiplying the square roots of each number.
Example: √(a × b) = √a × √b
- Quotient Rule: The square root of a fraction is the same as the square root of the numerator divided by the square root of the denominator.
Example: √(a/b) = √a / √b
- Square of a Square Root: Taking the square root of a squared number brings you back to the original number’s absolute value.
- Example: √(a²) = |a|
- Non-negative Roots: Square roots are only real and non-negative for non-negative numbers.
- Example: √a is real only if a ≥ 0
- Zero’s Square Root: The square root of zero is zero.
- Example: √0 = 0
- Square Root of One: The square root of one is one.
- Example: √1 = 1
- Adding and Subtracting: You can only directly add or subtract square roots if the numbers inside the square root (radicands) are the same.
- Example: √a + √a = 2√a
- Irrational Numbers: The square root of a non-perfect square is an irrational number, which cannot be exactly represented as a fraction or a terminating or repeating decimal.
- Example: √2 is irrational.
Square Root of a Negative Number
The concept of the square root of a negative number introduces us to the realm of complex numbers. In traditional real number arithmetic, a square root of a negative number does not exist because no real number squared gives a negative result. However, in the complex number system, there is a special number denoted as “i,” known as the imaginary unit, which is defined by the property that i2=−1.
Understanding the Imaginary Unit “i”
- The square root of -1 is defined as i.
- Therefore, the square root of any negative number can be expressed in terms of i. For example, √−4 can be written as √4×√−1 or 2i.
Example
Let’s calculate the square root of √-16:
- First, ignore the negative sign and find the square root of 16, which is 4.
- Since the number was negative, we then multiply our result by i to get the final answer.
- Therefore, −16=4i.
Square Root of Perfect squares
Perfect squares are the squares of whole numbers. The square root of a perfect square is always a whole number.
1² = 1 ⇔ √1 = 1
2² = 4 ⇔ √4 = 2
3² = 9 ⇔ √9 = 3
4² = 16 ⇔ √16 = 4
5² = 25 ⇔ √25 = 5
6² = 36 ⇔ √36 = 6
7² = 49 ⇔ √49 = 7
8² = 64 ⇔ √64 = 8
9² = 81 ⇔ √81 = 9
10² = 100 ⇔ √100 = 10
Square Root of Decimal
The square root of a decimal follows the same basic principle as finding the square root of whole numbers: it’s about finding a number that, when multiplied by itself, results in the original decimal. However, because the original number is a decimal, the square root will often be a decimal as well.
Example: Find the Square Root of 0.09
- Start with the Equation: Let’s say we want to find N where N²=0.16.
- Take the Square Root of Both Sides: This gives us N=±0.16.
- Understand the Multiplication: We know that 0.4×0.4=(0.4)²=0.16
- Simplify: So, N=±(0.4)².
- Conclude: Therefore, N=±0.4.
Applications of Square Roots
1. Mathematics and Geometry
- Pythagorean Theorem: One of the most classic applications of square roots is in the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Calculating the length of any side involves taking the square root of a number.
- Solving Quadratic Equations: Square roots are essential in solving quadratic equations. When determining the roots of a quadratic equation of the form ax^2 + bx + c = 0, the quadratic formula involves square roots.
2. Physics and Engineering
- Calculating Velocity and Acceleration: In physics, square roots are used to calculate the velocity of an object when its acceleration and the time taken are known. Similarly, they are used in formulas to find the distance covered under constant acceleration.
- Resonance Frequencies: In engineering, particularly in electrical engineering, square roots are used to calculate resonance frequencies of circuits, which is crucial for designing filters and oscillators.
3. Computer Graphics
- Distance Between Points: Square roots are used to calculate the distance between two points in space, whether in 2D or 3D. This is essential in computer graphics for rendering scenes accurately and in developing games to calculate movements or distances between objects.
4. Statistics and Data Analysis
- Standard Deviation: In statistics, the square root is used in the calculation of the standard deviation, which measures the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.
5. Finance
- Compound Interest: In finance, square roots (or roots in general) are used to calculate the time it takes for an investment to grow to a certain amount or to calculate the interest rate required to achieve a certain growth over a specified period.
6. Architecture and Design
- Golden Ratio: The square root of 5 is a key component in the golden ratio, a proportion often used in art, architecture, and design for its aesthetically pleasing properties. The golden ratio is believed to represent the most aesthetically pleasing proportion between two quantities.
7. Medicine and Health Sciences
- Drug Dosage Calculations: In health sciences, square roots are sometimes used in calculating the correct dosage of drugs, especially in determining the area of a patch for transdermal medication delivery based on the dosage rate.
What Is a Square Number in Math?
A square number is a number obtained when an integer is multiplied by itself.And It is also referred to as “a perfect square.”
Multiplying two positive integers together yields a positive result. And similarly, when two negative integers are multiplied, the outcome is also positive.
(+) × (+) = (+)
(-) × (-) = (+)
Examples of square numbers:
4 × 4 =16
(-5) × (-5) = 25
How to find Square Numbers ?
square numbers involves a simple process based on the definition of what a square number is. A square number, or a perfect square, is the product of an integer multiplied by itself. Here’s how you can find square numbers:
- Choose an Integer: Select any integer. This could be a positive number, a negative number, or zero.
- Multiply the Integer by Itself: Use the multiplication operation to multiply the chosen integer by itself. The formula for this is N², where N is the integer you’ve chosen.
- Result: The result of this multiplication is a square number. For instance, if you select 4 as your integer, multiplying 4 by itself (i.e., 4×4 or 4²) gives you 16, which is a square number.
Examples:
- 1²=1
- 2²=4
- 3²=9
- 10²=100
Properties of Square Numbers
- Last Digit Characteristics: Only the numerals 0, 1, 4, 5, 6, or 9 can appear as the final digit in square numbers, excluding those ending in 2, 3, 7, or 8 from being perfect squares.
- Ending Zeros in Squares: Perfect squares must feature zeros in pairs at their conclusion, disqualifying numbers with a solitary or odd tally of zeros at the end, such as 20, 360, or 480, unlike valid squares like 900 and 4900.
- Outcome of Squaring Specific End Digits: Numbers concluding in 1 or 9 yield squares that terminate in 1, whereas those ending in 4 or 6 result in squares concluding in 6.
- Parity of Square Numbers: The square of an even numeral remains even, and conversely, squaring an odd number produces an odd result, affirming the non-negative nature of square numbers.
- Positivity of Squares: The nature of squaring ensures all square numbers manifest as positive values.
- Criteria for Perfect Squares: A numerical value whose square root emerges as a fraction or a decimal is not recognized as a perfect square, exemplified by the fact that 0.25 does not qualify as a square number.
List of Square Numbers (1 to 100)
| Number – Square | Number – Square | Number – Square | Number – Square | Number – Square |
|---|---|---|---|---|
| 1²= 1 | 21²=441 | 41²=1681 | 61²=3721 | 81²=6561 |
| 2²=4 | 22²=484 | 42²=1764 | 62²=3844 | 82²=6724 |
| 3²=9 | 23²=529 | 43²=1849 | 63²=3969 | 83²=6889 |
| 4²=16 | 24²=576 | 44²=1936 | 64²=4096 | 84²=7056 |
| 5²=25 | 25²=625 | 45²=2025 | 65²=4225 | 85²=7225 |
| 6²=36 | 26²=676 | 46²=2116 | 66²=4356 | 86²=7396 |
| 7²=49 | 27²=729 | 47²=2209 | 67²=4489 | 87²=7569 |
| 8²=64 | 28²=784 | 48²=2304 | 68²=4624 | 88²=7744 |
| 9²=81 | 29²=841 | 49²=2401 | 69²=4761 | 89²=7921 |
| 10²=100 | 30²=900 | 50²=2500 | 70²=4900 | 90²=8100 |
| 11²=121 | 31²=961 | 51²=2601 | 71²=5041 | 91²=8281 |
| 12²=144 | 32²=1024 | 52²=2704 | 72²=5184 | 92²=8464 |
| 13²=169 | 33²=1089 | 53²=2809 | 73²=5329 | 93²=8649 |
| 14²=196 | 34²=1156 | 54²=2916 | 74²=5476 | 94²=8836 |
| 15²=225 | 35²=1225 | 55²=3025 | 75²=5625 | 95²=9025 |
| 16²=256 | 36²=1296 | 56²=3136 | 76²=5776 | 96²=9216 |
| 17²=289 | 37²=1369 | 57²=3249 | 77²=5929 | 97²=9409 |
| 18²=324 | 38²=1444 | 58²=3364 | 78²=6084 | 98²=9604 |
| 19²=361 | 39²=1521 | 59²=3481 | 79²=6241 | 99²=9801 |
| 20²=400 | 40²=1600 | 60²=3600 | 80²=6400 | 100²=10000 |
Two-digit Square Numbers
Two-digit square numbers are the squares of integers that result in values between 10 and 99.
- 4²=16
- 5²=25
- 6²=36
- 7²=49
- 8²=64
- 9²=81
Three-digit Square Numbers
- 10²=100
- 11²=121
- 12²=144
- 13²=169
- 14²=196
- 15²=225
- 16²=256
- 17²=289
- 18²=324
- 19²=361
- 20²=400
- 21²=441
- 22²=484
- 23²=529
- 24²=576
- 25²=625
- 26²=676
- 27²=729
- 28²=784
- 29²=841
- 30²=900
- 31²=961
Odd and Even Square Numbers
- Even Square Numbers: When an even number is squared (e.g,2,4,6,…), the result is always an even square number. This is because the multiplication of any two x (and squaring an even number is essentially multiplying it by itself) will always result in an even number. For example, 4²=16 and 6²=36 are both even square numbers.
- Odd Square Numbers: Conversely, when an odd number is squared (e.g., 1,3,5,…), the result is always an odd square number. This occurs because the product of any two odd numbers remains odd. For instance, 3²=9 and 5²=25 are odd square numbers.
Square Numbers and Multiplication Arrays
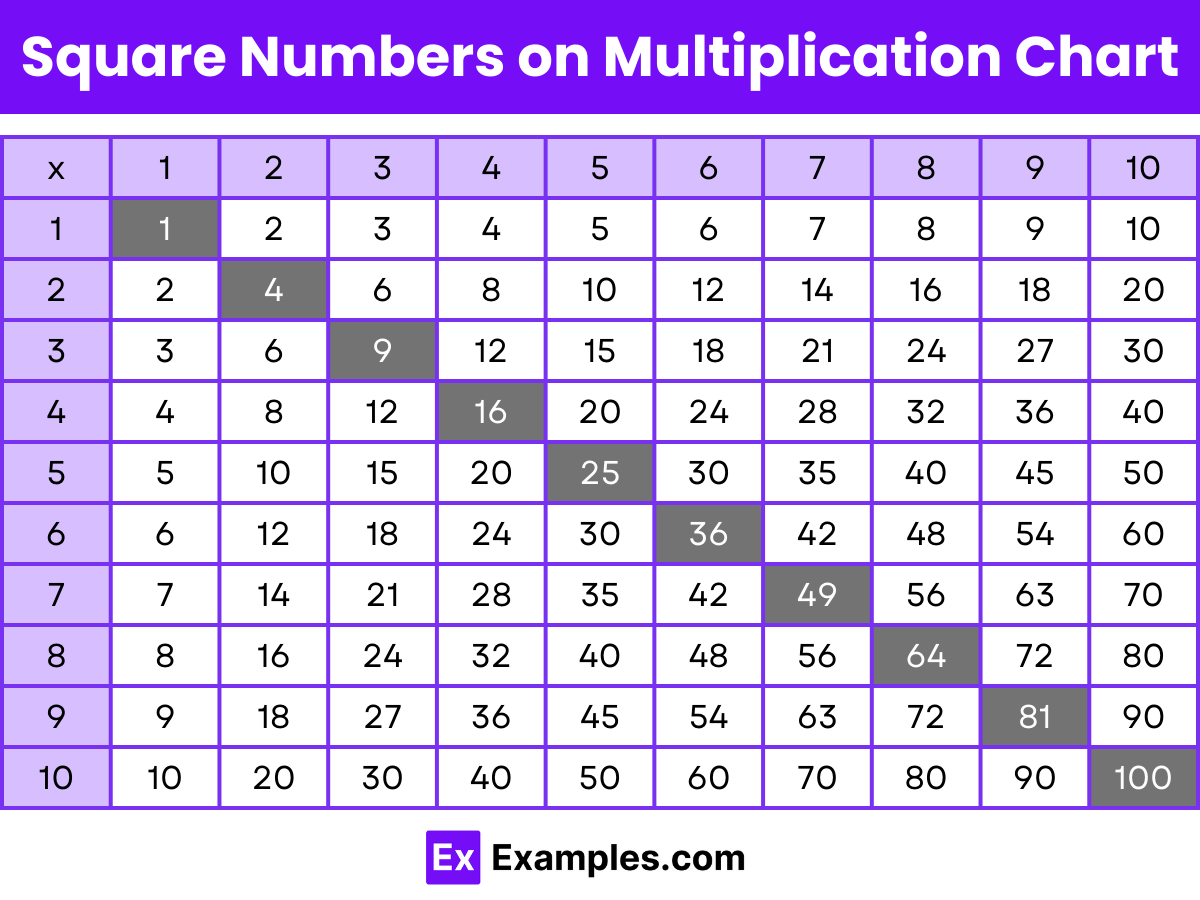
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Facts about Square Numbers
- Square of a Sum: The square of the sum of two numbers can be expanded as (a+b)²=a²+2ab+b². This formula is a cornerstone in algebra, illustrating how two quantities, when squared together, yield not just their individual squares but also a combined term.
- Square of a Difference: Similarly, the square of the difference between two numbers is expressed as (a−b)²=a²−2ab+b². This highlights the symmetrical nature of algebraic operations, even when dealing with subtraction.
- Difference of Squares: A powerful algebraic identity is the difference of squares a²−b²=(a+b)(a−b). This shows that the difference between any two square numbers can be factored into a product of their sum and difference.
- Pythagorean Theorem: In algebra, square numbers play a crucial role in the Pythagorean theorem, a²+b²=c², where c is the hypotenuse of a right triangle, and a and b are the other two sides. This theorem is a practical application of square numbers in geometry.
- Perfect Square Trinomials: Algebra introduces the concept of perfect square trinomials, expressions that can be factored into the square of a binomial. For example, x²+2xy+y² can be factored as (x+y)², showcasing how algebraic expressions can represent square numbers.
- Square Root Function: The square root function, denoted as √x, is fundamental in algebra for finding the original number that was squared. This function highlights the inverse relationship between squaring and finding a square root.
- Integral Solutions: Square numbers are integral in solving quadratic equations, where the solution involves finding the square root of a number. This can lead to integral or real solutions, depending on the discriminant.
- Sum of Consecutive Odd Numbers: Algebraically, it can be shown that any square number is the sum of consecutive odd numbers starting from 1, a property that illustrates the progressive addition of layers to form squares.
FAQs
How Do I Calculate Square Root?
To calculate the square root of a number, you can use methods like prime factorization, the long division method, or a calculator. This operation finds the number which, when squared, equals the original number.
What Happens When You Put a Square and Square Root Together?
Applying a square and a square root operation successively to a number generally returns the original number, provided the operations are executed in sequence on non-negative numbers.
How to Solve √50?
To solve √50, simplify it by expressing 50 as 25 × 2. Since √25 is 5, √50 simplifies to 5√2, which is an exact and simplified form.
Can We Add √2 + √3?
Yes, you can add √2 and √3, but they cannot be simplified to a single radical or whole number. The result is simply expressed as √2 + √3.
Can We Add √2 * √2?
Yes, you can multiply √2 by √2. The result of this multiplication is 2, as the square root and the squaring operation cancel each other out.
Share :
