What is the square of 6?
32
36
40
42
of 10
Square & Square Root of 6 – Methods, Calculation, Formula, How to find
Square of 6
6² (6×6) = 36
To calculate the square of 6, you simply multiply 6 by itself:
The square of 6 is the result of multiplying 6 by itself. In mathematical terms, it is written as 6², which equals 36. So, the square of 6 is 36. It represents the area of a square with sides of length 6 units.
Square Root of 6
Or
√6=2.449 up to three places of decimal
The square root of 6, denoted as √6, refers to the positive number that,, meaning it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating. The approximate value of the square root of 6 is approximately 2.44948974278. In other words, if you multiply this number by itself, you get approximately 6.
The square root of 6 finds applications in various fields such as mathematics, physics, engineering, and finance. It’s particularly useful in geometry for calculating side lengths or areas of shapes where the value of √6 is involved.
Exponential Form: 6^½ or 6^0.5
Radical Form: √6
Is the Square Root of 6 Rational or Irrational?
The square root of 6 is an irrational number.
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a number that cannot be expressed as a ratio of two integers, and its decimal representation goes on infinitely without repeating.
- In the case of the square root of 6 (√6), its exact decimal representation is approximately 2.44948974278, and it continues indefinitely without a repeating pattern.
- Since it cannot be expressed as a fraction of two integers and its decimal representation is non-repeating and non-terminating, √6 is classified as an irrational number.
The square root of 6 (√6) cannot be expressed as a fraction of two whole numbers (such as 2/3, 5/7, etc.). It’s a number that goes on forever without repeating any pattern when written as a decimal.
So, in simpler terms, the square root of 6 is irrational. It doesn’t fit into the category of rational numbers, which can be expressed as fractions. Instead, it’s a bit more complex and doesn’t follow a simple pattern in its decimal representation.
Methods to Find Value of Root 6
Finding the Methods to determine the value of the square root of 6 involve various mathematical approaches or techniques aimed at approximating or calculating its numerical value. These methods may include iterative algorithms, the use of calculators, mathematical tables, or numerical estimation techniques.
Estimation Method
The estimation method for finding the value of the square root of 6 involves approximating its numerical value using techniques such as rounding, comparison with known square roots, or using mathematical properties to get close approximations.
- Start with an initial guess. Since 6 is between 2^2 (which is 4) and 3^2 (which is 9), you know that the square root of 6 is between 2 and 3.
2. Calculate and Take a number between 2 and 3, say 2.5, and square it: 2.5 * 2.5 = 6.25.
3. Since 6.25 is higher than 6, you need to try a smaller number. You can repeat this process with smaller increments or use methods like Newton’s method for faster convergence.
4. Refine to Continue adjusting your guess until you get close to the actual value. You can use a calculator or software to get a more accurate result.
5. Check Once you have a refined estimate, you can check by squaring it again to see if it’s close to 6.
Square Root of 6 by Long Division Method
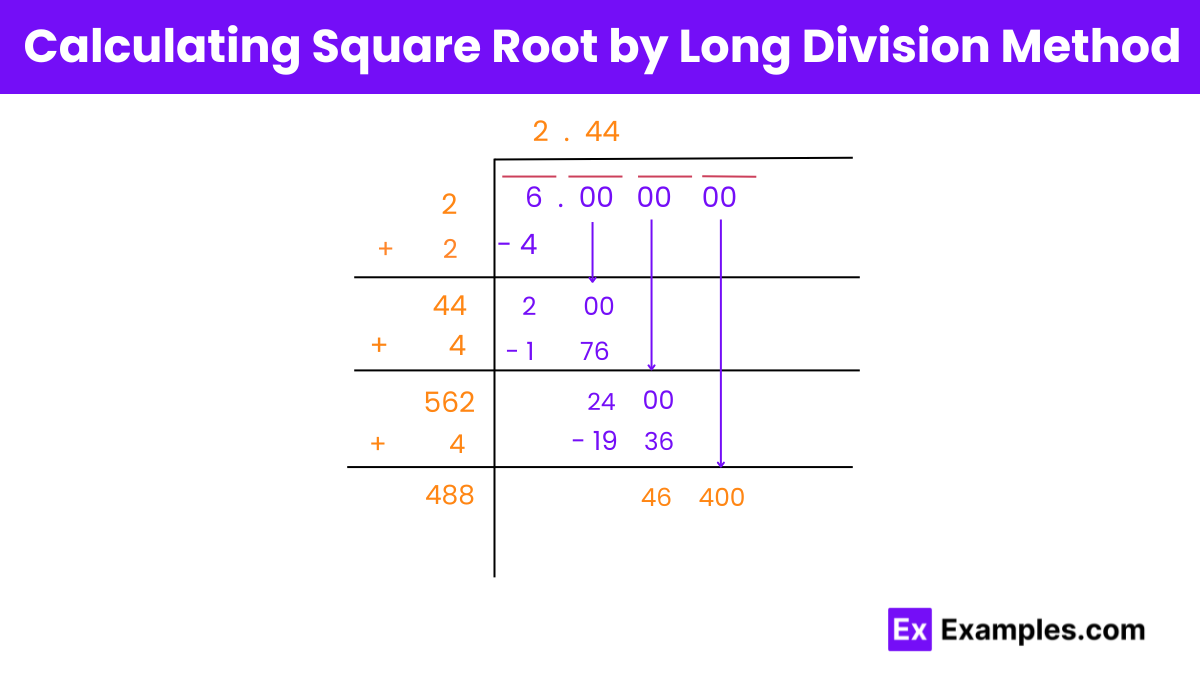
Step 1: Initial Guess
- Start with an educated guess based on the range of possible square roots.For √6, since 6 lies between 2² and 3², begin with the guess of 2.
Step 2: Square the Guess
- Square the initial guess to obtain the closest square less than 6.
- 2 * 2 = 4.
Step 3: Subtract and Remainder
- Subtract the result from 6 to find the remainder.
- 6 – 4 = 2.
Step 4: Bring Down the Next Pair
Bring down the next pair of digits (00) to continue the calculation.
Step 5: Double and Trial Division
- Double the current guess and perform trial division to refine the approximation.Doubling 2 gives 4; the closest digit to append is 5, yielding a new guess of 2.5.
Step 6: Square the New Guess
- Square the updated guess to check proximity to the original number.
- 2.5 * 2.5 = 6.25.
Step 7: Adjustment and Final Approximation
- Adjust the guess based on the squared value; since it’s greater than 6, revert to the previous digit.
- The approximate square root of 6 is 2.45.
FAQs Short Question & Answers
What are some practical applications of the square root of 6?
The square root of 6 is used in various fields such as mathematics, physics, engineering, and finance. It is particularly useful in geometry for calculating side lengths or areas of shapes involving √6.
How can I calculate the square root of 6?
The square root of 6 can be approximated using methods like long division, Newton’s method, or through the use of calculators and software.
Can the square root of 6 be simplified further?
No, the square root of 6 is an irrational number and cannot be simplified into a simpler form involving whole numbers or fractions.
Are there any real-world examples where √6 is relevant?
Yes, √6 can be relevant in real-world scenarios such as calculating distances, dimensions, or quantities in various fields including architecture, construction, and surveying.
Share :
Practice Test
Which number is closest to the square root of 6?
2.4
2.5
2.6
2.7
of 10
If x² = 6, what is x?
2.4
2.5
2.6
2.7
of 10
What is √6 rounded to the nearest whole number?
2
3
4
5
of 10
Calculate 6².
30
32
34
36
of 10
Find √6 to two decimal places.
2.43
2.45
2.47
2.49
of 10
If you multiply √6 by itself, what result do you get?
6
12
18
24
of 10
Which of the following numbers is not close to the square root of 6?
2.4
2.5
2.6
2.8
of 10
What is the approximate value of √6 when expressed as a fraction?
2.45/1
2.5/1
2.4/1
2.4/1.1
of 10
Determine the value of (√6)².
5
6
7
8
of 10