Square & Square Root of 8
Square of 8
To calculate the square of 8, you simply multiply 8 by itself:
Therefore, the square of 8 is 64. This straightforward calculation is a building block for more complex mathematical operations and concepts, including algebraic equations, geometric formulas, and statistical models.
Square Root of 8
Or
√8 = 2.828 up to three places of decimal
The square root of 8, symbolized as √8, holds a fascinating position in mathematics, showcasing the intriguing world of irrational numbers. When we talk about square roots, we refer to finding a number that, when squared (multiplied by itself), equals 8. The square root of 8 can also be represented in exponential form as 8^½ or 8^⁰.⁵ This number, precise to eight decimal places, is 2.82842712, and it serves as a positive solution to the equation x² = 8.
Square Root of 8: 2.8284271247461903
Exponential Form: 8^½ or 8^0.5
Radical Form: √8 or 2√2
Is the Square Root of 8 Rational or Irrational?
The square root of 8 is an irrational number. This can be understood by breaking down what rational and irrational numbers are:
- A rational number is any number that can be expressed as a fraction a/b where a and b are integers, and b is not equal to zero. It includes integers, fractions, and finite or repeating decimals.
- An irrational number is a number that cannot be expressed as a simple fraction. Irrational numbers have non-repeating, non-terminating decimal expansions.
To see why the square root of 8 is irrational, let’s first simplify it:
√8=√4⋅2=√4⋅√2=2√2
We know that 22 is a rational number. However, 22 is famously irrational. It cannot be represented as a fraction of two integers, and its decimal form goes on forever without repeating. Therefore, 2√2 is also irrational, because the product of a rational number (in this case, 22) and an irrational number (√2) is always irrational.
To summarize, the square root of 8 is irrational because it can be simplified to 2√2, which involves the square root of 2 – a well-known irrational number
Method to Find Value of Root 8
To find the square root of 8, we can use several methods, including estimation, the prime factorization method, and using a calculator. Here, we focus on a simple estimation method for understanding:
- Identify Perfect Squares Around 8: Recognize that the perfect square closest to but less than 8 is 4 (2²=4), and the perfect square closest to but more than 8 is 9 (3²=9).
- Estimation: Since 8 is between 4 and 9, its square root will be between 2 and 3.
- Refinement: To get a more precise value, use a calculator or a square root table. The square root of 8 is approximately 2.8284271247461903.
- Simplified Radical Form: The square root of 8 can also be expressed in simplified radical form as √8=√4×2=2√2.
Square Root of 8 by Long Division Method
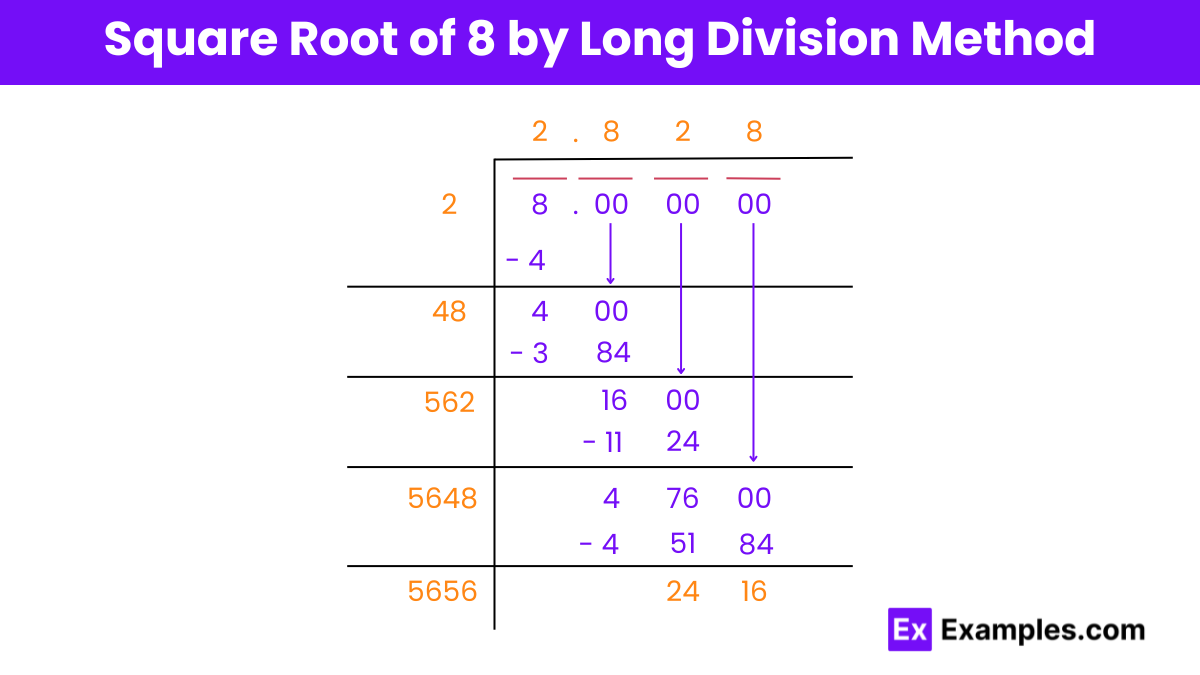
Step 1: Preparation
Write 8 as 8.00 00 00, grouping digits in pairs from the decimal point. For 8, it looks like “08”.
Step 2: Find the Largest Square
Identify the largest square smaller than or equal to 8, which is 4 (2²). Place 2 above the line as the first digit of the root.
Step 3: Subtract and Bring Down
Subtract 4 from 8 to get 4, then bring down the next pair of zeros to make it 400.
Step 4: Double and Find the Next Digit
Double the current result (2) to get 4. Now, find a digit (X) such that 4X multiplied by X is less than or equal to 400. Here, X is 8, because 48×8=384
Step 5: Repeat with Precision
Subtract 384 from 400 to get 16, bring down the next zeros to get 1600, then double the quotient (28) to get 56. Choose a digit (Y) so 56Y×Y is just under 1600.
Step 6: Finish at Desired Accuracy
Continue the process until reaching the desired level of accuracy. For the square root of 8, this method gives us about 2.828 as we extend the division.
Share :
