Square & Square Root of 95
Square & Square Root of 95
Square of 95
The square of 95 refers to the result of multiplying the number 95 by itself. In mathematical terms, this is expressed as (95 × 95). Square number is one of the basic operations in arithmetic and algebra, serving as a fundamental concept for building more complex mathematical ideas. When you square 95, you get 9025. This calculation helps illustrate properties of exponents and powers, which are crucial for understanding more advanced topics in mathematics such as quadratic equations, power functions, and polynomial identities.
Square Root of 95
The square root of 95 is the number that, when multiplied by itself, equals 95. Mathematically, this is expressed as √95. The exact square root of 95 is an irrational number, since it cannot be expressed as a simple fraction. Understanding the square root is crucial in mathematics because it helps in solving problems that involve areas, particularly when dealing with squares and square-shaped objects. Knowing how to find and apply square roots is essential in fields ranging from geometry to physics, where it is used to unravel various practical and theoretical problems.
Exponential Form of 95: (95^1/2) or (95^0.5)
Radical Form of 95: √95
Is the Square Root of 95 Rational or Irrational?
Irrational number means it cannot be expressed as a fraction of two integers.
A rational number is defined as one that can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero.
Methods to Find the Value of Root 95
To find the value of the square root of 95, you can use several methods. Here are two common approaches:
1. Long Division Method:
- Set up the number in pairs of digits starting from the decimal point: (95.000000) (consider as many decimal places as needed for precision).
- Find the largest integer whose square is less than or equal to 95: (9 × 9 = 81). Write 9 as the quotient and 81 under 95, then subtract to get a remainder of 14.
- Bring down the next pair of zeros (to make 1400).
- Double the quotient (9) and write it as the new divisor’s leading digit: (18_ ).
- Find the largest digit (D) to fill in the blank such that (18D × D) is less than or equal to 1400: (182 × 2 = 364). Write 2 next to the 9 in the quotient.
- Subtract to find the new remainder: (1400 – 364 = 1036).
- Repeat the process by bringing down pairs of zeros and finding the next digits.
2. Calculator Method:
- Enter 95 into a calculator.
- Press the square root (√) button.
- The calculator will display the square root of 95: approximately (9.74679434481).
Using these methods, you can determine that the square root of 95 is approximately (9.74679434481).
Square Root of 95 by Long Division Method
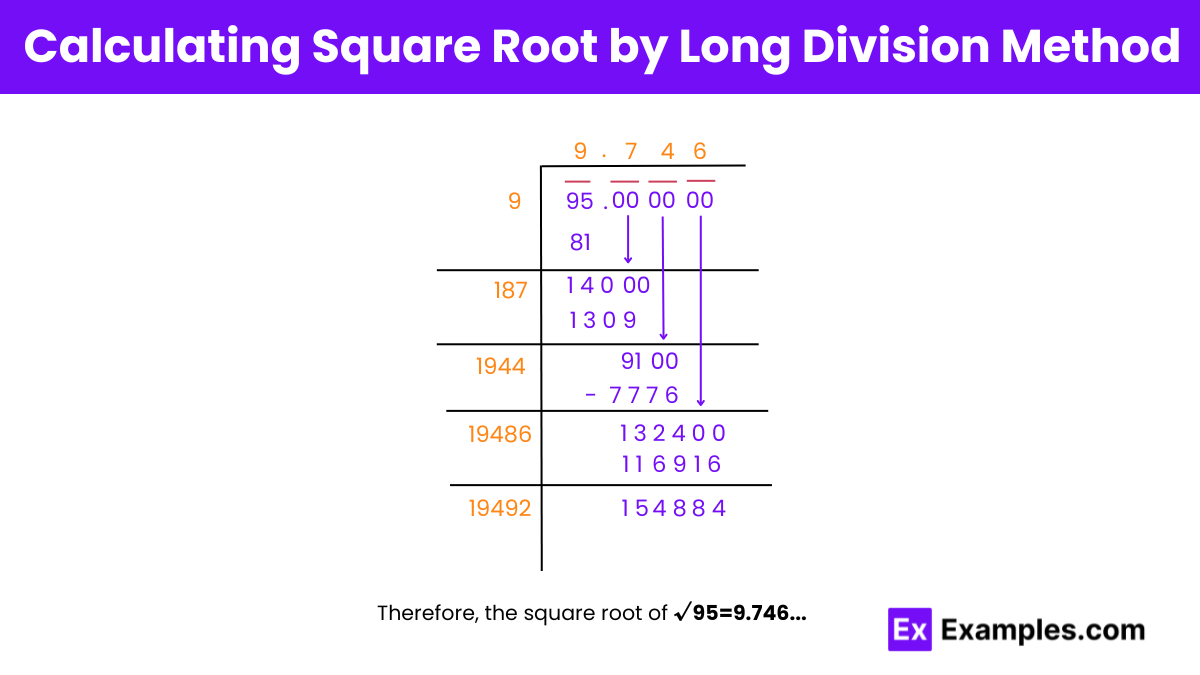
Step 1: Writing 95 as 95.00 00 00,
Step 2: Finding a number × number that gives the product 95 or less than that.
Step 3: We know that (9 × 9 = 81). Subtracting this from 95, we get the remainder as 14. Bringing down the pair of zeros, 1400 is our new dividend.
Step 4: Doubling the quotient, we obtain 18. To find the new divisor, (18n × n) should be less than or equal to 1400.
Step 5: We determine that (187 × 7 = 1309). Subtracting this from 1400, we obtain the remainder as 91. Bringing down the next pair of zeros, 9100 is the new dividend.
Step 6: Doubling the quotient (9.7), we obtain 194, and let us have (194n × n) as our new divisor.
Step 7: We determine (1944 × 4 = 7776) as our product. Subtracting this from 9100, we obtain 1324 as the remainder. Bringing down the next pair of zeros.
Step 8: Repeating the process until we obtain the quotient approximated to 3 decimal places.
√95 = ± 9.746
95 is Perfect Square root or Not?
A perfect square is a number that can be expressed as the square of an integer. Since there is no integer whose square equals 95, it is not a perfect square.
FAQS
Which number is closest to the square root of 95?
The number closest to the square root of 95 is approximately 9.746.
What numbers are between √ 95?
Between √95 and √96, the numbers are:
(9.746 < x < 9.798)
So, the numbers between √95 are approximately 9.747 to 9.798.
What are the factors of 95?
The factors of 95 are the numbers that divide evenly into 95 without leaving a remainder. The factors of 95 are 1, 5, 19, and 95.
What is the square root of 95 to the nearest tenth?
The square root of 95 to the nearest tenth is approximately 9.7.
Share :
