What is the degree measure of a right angle?
30 degrees
45 degrees
60 degrees
90 degrees
of 10
Degree – Examples, Formula, Usages, Applications
Degree – Examples, Formula, Usages, Applications
What is Degree ?
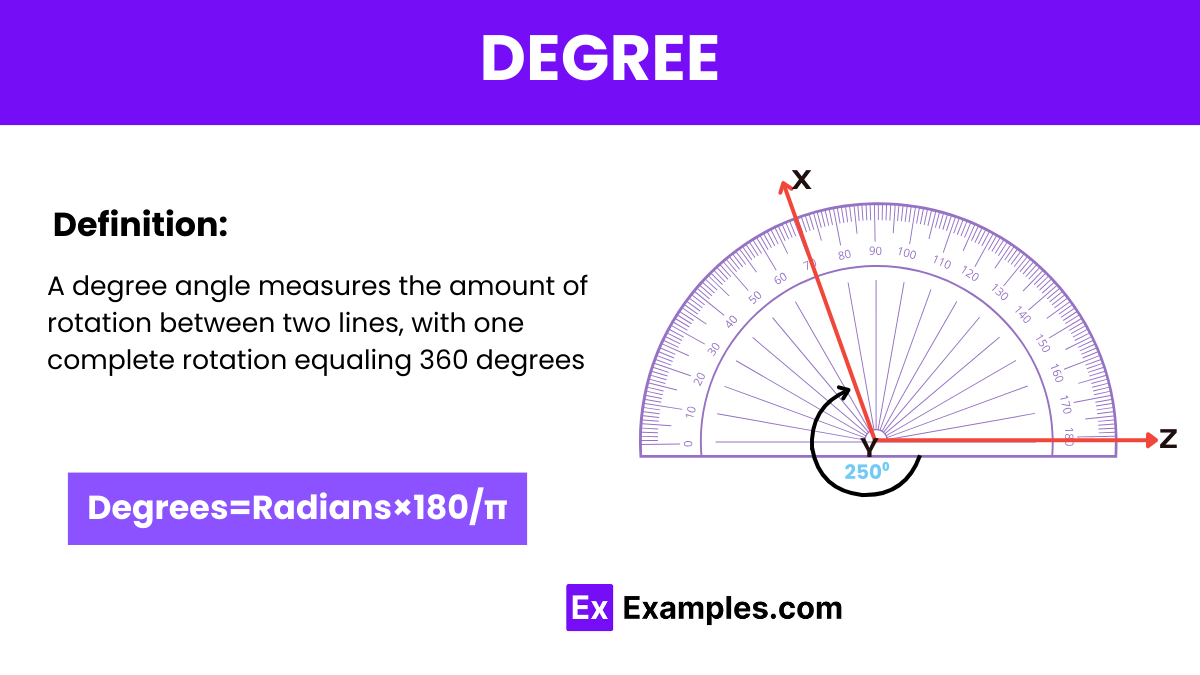
Degree is a unit of angular measurement equal to 1/360th of a full rotation. It is commonly used to express angles and rotations in various fields such as astronomy, engineering, and geometry.
Additional Formula
Arc Length Formula
Sector Area Formula
Tangent of Angle Sum
Cosine of Double Angle
Sine of Double Angle
Applications of Degree
- Engineering: Used to measure angles in construction, mechanical engineering, and structural design.
- Physics: Essential for describing rotational motion, including the rotation of objects and the measurement of angles in various physical phenomena.
- Astronomy: Utilized for celestial navigation, describing the positions of celestial bodies, and measuring the apparent size of objects in the sky.
- Navigation: Crucial for determining direction and bearing, especially in marine and aviation navigation systems.
- Trigonometry: Fundamental for solving problems involving triangles and periodic phenomena, such as waveforms and oscillations.
- Cartography: Used in map-making to define the direction and orientation of features on maps and globes.
- Geography: Employed to describe the direction of geographical features and determine the layout of geographical regions.
- Computer Graphics: Degrees are used to represent angles in computer graphics systems for rendering images and animations.
- Surveying: Essential for measuring angles and distances accurately in land surveying and geodetic surveying.
- Robotics: Degrees are used to define the orientation and movement of robotic arms and other robotic systems.
Conversion of Degree into Other Units
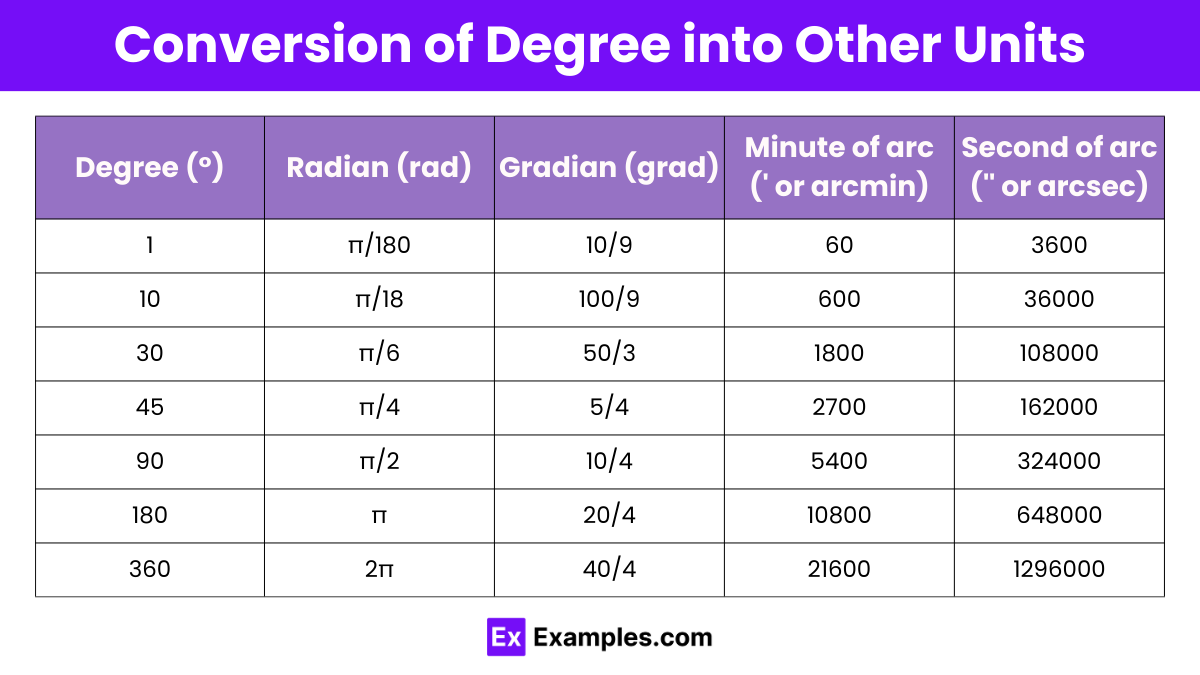
| Degree (°) | Radian (rad) | Gradian (grad) | Minute of arc (‘ or arcmin) | Second of arc (” or arcsec) |
|---|---|---|---|---|
| 1 | π/180 | 10/9 | 60 | 3600 |
| 10 | π/18 | 100/9 | 600 | 36000 |
| 30 | π/6 | 50/3 | 1800 | 108000 |
| 45 | π/4 | 5/4 | 2700 | 162000 |
| 90 | π/2 | 10/4 | 5400 | 324000 |
| 180 | π | 20/4 | 10800 | 648000 |
| 360 | 2π | 40/4 | 21600 | 1296000 |
Degree (°) to Radian (rad)
One degree (°) is equivalent to π/180 radians (rad). This conversion factor allows for easy interchange between degrees and radians.
Degree (°) to Gradian (grad)
One degree (°) equals 10/9 gradians (grad). This conversion factor facilitates the interchange between degrees and gradians in angular measurements.
Degree (°) to Minute of arc (‘ or arcmin)
One degree (°) equals 60 minutes of arc (‘), commonly used in navigation, astronomy, and geographical coordinates for finer angular measurements.
Degree (°) to Second of arc (” or arcsec)
1 Degree (°) equals 3600 seconds of arc (” or arcsec), making it a fundamental unit for measuring angles in trigonometry and astronomy.
Uses of Degree
- Navigation: Essential for determining directions and bearings, aiding in marine and aviation navigation.
- Engineering: Used in construction, structural design, and mechanical engineering to measure angles and alignments.
- Astronomy: Crucial for celestial navigation, describing the positions of celestial bodies, and measuring apparent sizes.
- Mathematics: Fundamental for trigonometric calculations, solving problems involving triangles, and analyzing periodic phenomena.
- Geography: Utilized to define directions, determine the layout of geographical features, and calculate distances.
- Cartography: Employed in map-making to represent the orientation and scale of features on maps and globes.
- Computer Graphics: Degrees are used to represent angles in computer graphics systems for rendering images and animations.
- Surveying: Important for measuring angles and distances accurately in land surveying and geodetic surveying.
FAQ’S
What are the 7 types of angles degrees?
- Acute angle: Measures between 0 and 90 degrees.
- Right angle: Measures exactly 90 degrees.
- Obtuse angle: Measures between 90 and 180 degrees.
- Straight angle: Measures exactly 180 degrees.
- Reflex angle: Measures between 180 and 360 degrees.
- Full angle: Measures exactly 360 degrees.
- Zero angle: Measures exactly 0 degrees.
How do you find degrees of angles?
Degrees of angles can be found using a protractor, which is a tool designed for measuring angles. Place the center of the protractor at the vertex of the angle, align the base line of the protractor with one side of the angle, and then read the degree measurement where the other side intersects with the protractor scale.
What is the degree measure of an angle?
The degree measure of an angle represents the amount of rotation between its two sides, usually measured in degrees. It indicates how much one side must be rotated about the vertex to coincide with the other side. This measure typically ranges from 0 to 360 degrees, with specific categories for different ranges of measure, as mentioned in the first point.
Share :
Practice Test
How many degrees are in a full circle?
180 degrees
270 degrees
360 degrees
540 degrees
of 10
What is the degree measure of an angle that is supplementary to a 75-degree angle?
105 degrees
115 degrees
75 degrees
45 degrees
of 10
How many degrees are in an equilateral triangle?
90 degrees
120 degrees
180 degrees
360 degrees
of 10
What is the measure of each angle in an equilateral triangle?
30 degrees
45 degrees
60 degrees
90 degrees
of 10
If an angle measures 130 degrees, what is its complement?
50 degrees
40 degrees
60 degrees
Complement does not exist
of 10
What is the degree measure of each interior angle of a regular pentagon?
90 degrees
108 degrees
120 degree
135 degrees
of 10
How many degrees are in the sum of the interior angles of a hexagon?
540 degrees
720 degrees
900 degrees
1080 degrees
of 10
What is the degree measure of each exterior angle of a regular octagon?
30 degrees
45 degrees
60 degrees
90 degrees
of 10
What is the degree measure of an angle that is the supplement of a 120-degree angle?
30 degrees
45 degrees
60 degrees
90 degrees
of 10