Kirchoffs second law – Definition, Formula, Advantages, FAQ’S

Kirchhoff’s Second Law, also known as Kirchhoff’s Voltage Law (KVL). It states that the sum of the electrical voltage gains and drops around any closed circuit loop must equal zero. This law, rooted in the principle of conservation of energy in physics. It ensures that the total energy around the loop is conserved, implying no net loss or gain in energy. Consequently, it serves as a fundamental rule for analyzing electrical circuits, enabling precise calculations of voltage distribution across circuit components.

Kirchhoff’s Voltage Law

Kirchhoff’s Laws

Kirchhoff’s Circuit Laws are two fundamental principles in electrical circuit theory that help in analyzing complex networks of conductors and components.

First Law : Kirchhoff’s Current Law (KCL) states that the total current entering a junction must equal the total current leaving the junction. This law is based on the principle of conservation of electric charge. Implying that no charge is lost at the junction; it merely redistributes.

Second Law : Kirchhoff’s Voltage Law (KVL) asserts that the total sum of all voltages around any closed loop in a circuit must equal zero. This follows from the law of conservation of energy, which stipulates that the total energy gained in traveling around the loop must be zero, ensuring that all energy supplied is used up.

Kirchhoff’s Voltage Law Formula

Kirchhoff’s Voltage Law (KVL) can be simply stated as the formula:

This means that the sum of all electromotive forces (EMFs) and voltage drops in a closed loop must equal zero. It ensures that the total voltage around any closed circuit path adds up to zero, reflecting the conservation of energy within the circuit.

Applying KVL in Complex Circuits

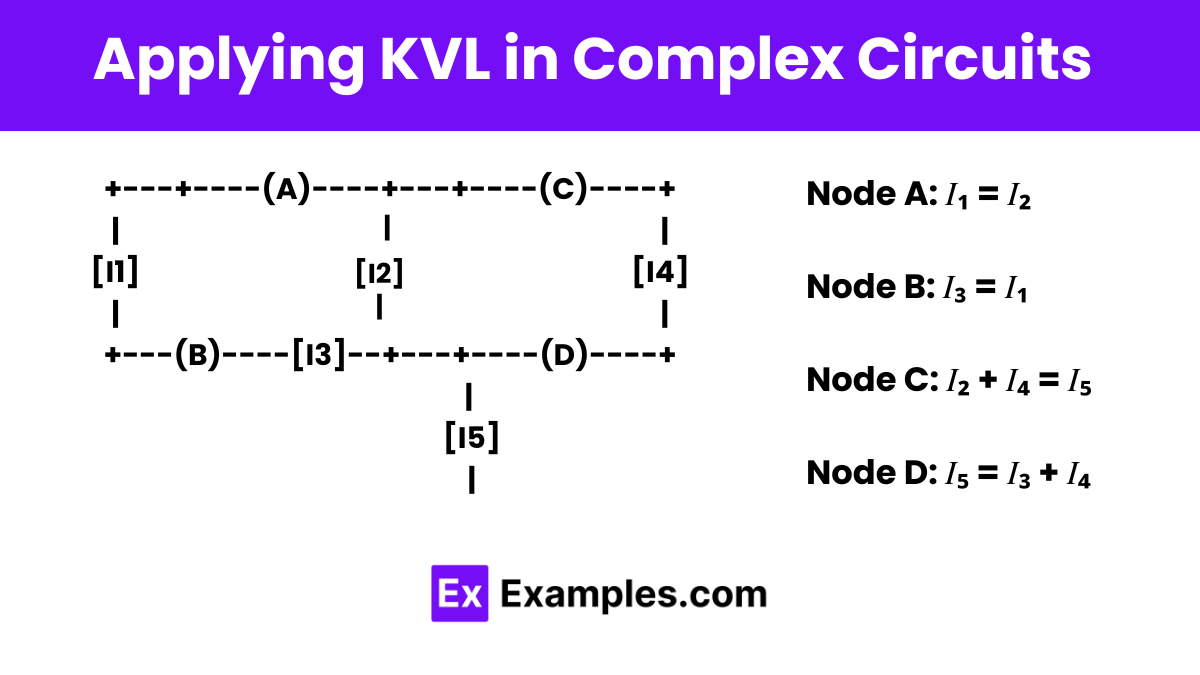
Applying Kirchhoff’s Voltage Law (KVL) in complex circuits involves a methodical approach to ensure that all voltages are accounted for accurately. Here’s a step-by-step guide on how to apply KVL to complex circuits:

Identify All Closed Loops

Start by identifying all the closed loops within the circuit. A complex circuit may include multiple loops, with smaller loops nested within larger ones, and each loop may share components with others.

Choose a Direction to Traverse the Loop

For each loop, choose a direction to traverse (clockwise or counterclockwise). Consistency in the direction helps in correctly applying the voltage signs (positive or negative) for each component.

List All Voltage Drops and Gains

As you traverse the loop in the chosen direction, list all the voltages across components such as resistors, capacitors, inductors, and any voltage sources like batteries or power supplies. Assign a positive value to voltage gains (such as those across a battery from negative to positive terminal) and a negative value to voltage drops (such as those across a resistor in the direction of current).

Apply the Voltage Law

Write down the equation for KVL: The sum of all voltages around the loop should be zero. This includes:

• Voltage gains from sources (batteries, generators)
• Voltage drops across resistive, capacitive, or inductive elements

Solve the Equations

If the circuit has multiple loops, you will end up with several KVL equations. Solve these simultaneous equations (often using methods like substitution or matrix techniques if the circuit is very complex) to find unknown quantities like current values or voltage drops.

Check for Consistency

Verify that the calculated values satisfy all the KVL equations for each loop. Consistency across all loops confirms the correctness of the solution.

Consider Real-World Factors

In practical scenarios, real-world factors such as resistance in wires, imperfect components, and other non-ideal behaviors should be considered. These factors might slightly modify the theoretical calculations.

Advantages of Kirchhoff’s Law

Kirchhoff’s Laws, comprising Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL), offer several advantages that make them indispensable tools in electrical engineering and physics. Here are the key benefits:

1. Comprehensive Analysis: Kirchhoff’s Laws provide a method for analyzing complex electrical circuits by breaking them down into simpler parts. They allow for the calculation of unknown currents, voltages, and resistances throughout the circuit, offering a complete understanding of circuit behavior.
2. Flexibility in Application: These laws are applicable to any type of electrical circuit, whether it involves direct current (DC) or alternating current (AC), and regardless of the complexity. This flexibility makes them universally useful in a wide range of electrical engineering tasks.
3. Foundation for Advanced Techniques: Kirchhoff’s Laws form the basis for more advanced circuit analysis methods like mesh and nodal analysis. These techniques, which are essential for handling more complex circuits, rely on the principles outlined in Kirchhoff’s Laws.
4. Accuracy in Problem Solving: By ensuring the conservation of charge and energy, Kirchhoff’s Laws enable highly accurate predictions of circuit behavior, which is critical for design and troubleshooting purposes.
5. Ease of Learning and Use: The laws are relatively simple to understand and apply, making them accessible to students and professionals alike. This ease of use encourages a systematic approach to circuit analysis that is both logical and effective.
6. Versatility in Electrical Network Analysis: They can be used not only for solving simple circuits but are also effective for analyzing large electrical networks, including those found in power distribution systems and complex electronics.

Limitations of Kirchhoff’s Law

While Kirchhoff’s Laws are incredibly useful for analyzing electrical circuits, they do have certain limitations that are important to consider, especially in more complex or specialized applications:

1. Ideal Conditions Assumed: Kirchhoff’s Laws assume that all components in the circuit are ideal, meaning there is no voltage drop across the wires and no resistance unless specified. In real-world applications, wires do have resistance and other components may have non-ideal behaviors which can lead to inaccuracies.
2. High Frequency Limitations: At very high frequencies, the assumptions underlying Kirchhoff’s Laws begin to break down due to the effects of electromagnetic fields and transmission line phenomena. Components like capacitors and inductors exhibit properties such as reactance and impedance which are not accounted for in simple Kirchhoff analysis.
3. Not Accounting for Electromagnetic Effects: Kirchhoff’s Laws do not take into account the electromagnetic effects such as inductance and capacitance unless explicitly included in the circuit as components. This can be a significant oversight in circuits where electromagnetic interactions are critical, such as in radio frequency (RF) circuits.
4. Complexity in Large Networks: While Kirchhoff’s Laws can technically be applied to any size of network, in practice, the complexity and number of equations required to solve large networks can be prohibitive without the use of sophisticated computational tools.
5. Nonlinear Components: Kirchhoff’s Laws are formulated for linear components and may not be directly applicable or may require modifications when dealing with nonlinear components like diodes and transistors which do not have a linear V-I relationship.
6. Assumption of Steady State: These laws are typically applied under the assumption of a steady state, where currents and voltages do not change over time. They do not inherently handle transient conditions where time-dependent changes are critical, such as during the power-up sequence in an electronic device.
7. Dependency on a Closed Loop: For Kirchhoff’s Voltage Law to be applied, a clear, closed loop must be identifiable in the circuit. In some complex or poorly defined circuits, determining these loops and correctly applying the law can be challenging.

FAQ’S

What are the first and second rules of Kirchhoff’s law?

Kirchhoff’s First Law (Current Law) states that the total current entering a junction equals the total current leaving. Kirchhoff’s Second Law (Voltage Law) asserts that the sum of all voltages around any closed loop in a circuit must equal zero.

What is 2 Kirchhoff’s second law based on the law of conservation of?

Kirchhoff’s Second Law is based on the law of conservation of energy, ensuring that the total energy around any electrical loop is conserved.

What is Kirchhoff’s second law loop law based on?

Kirchhoff’s Second Law, or the loop law, is grounded in the law of conservation of energy, affirming that energy within a closed circuit loop is neither created nor destroyed.