Boyles Law – Examples, Definition, Derivation, Uses, FAQ’s

Boyle’s Law is a fundamental principle in the field of physics, specifically within the realm of Laws of Thermodynamics and gas laws. This law states that the pressure of a given mass of an ideal gas is inversely proportional to its volume when the temperature remains constant. In simpler terms, if you increase the volume of a gas container, the pressure of the gas decreases, provided the temperature does not change.

What is Boyle’s Law?

Boyles Law Formula

Formally expressed, Boyle’s Law is: 𝑃×𝑉=constant, where P represents the pressure of the gas, and 𝑉 denotes the volume. This relationship is a cornerstone in the laws of physics, showcasing how gases behave under varying pressures and volumes, and is crucial in applications ranging from respiratory physiology to engineering.

The formula for Boyle’s Law is expressed as:

Where:

• 𝑃₁​ is the initial pressure exerted by the gas,
• 𝑉₁ is the initial volume occupied by the gas,
• 𝑃₂​ is the final pressure exerted by the gas,
• 𝑉₂ is the final volume occupied by the gas.

This equation demonstrates that for a given amount of gas at a constant temperature, the product of the pressure and volume remains constant, even as the individual values of pressure and volume change

Derivation of Boyles Law

Boyle’s Law states that the pressure and volume of a gas have an inverse relationship when temperature is held constant. Here is a concise derivation:

Starting Point: Assume the gas is ideal and that its temperature remains constant.

Ideal Gas Law: For a constant amount of gas at constant temperature, the ideal gas law 𝑃𝑉=𝑛𝑅𝑇 simplifies because 𝑛 (number of moles), 𝑅 (gas constant), and 𝑇 (temperature) are constants.

Constant Product: With 𝑛𝑅𝑇 being constant, 𝑃𝑉 is also constant. Thus, if the volume 𝑉 increases, the pressure 𝑃 must decrease proportionally to maintain the equality, and vice versa.

Mathematical Expression: This relationship can be expressed as: 𝑃₁𝑉₁=𝑃₂𝑉₂ Here, 𝑃₁ and 𝑉₁​ are initial pressure and volume, and 𝑃₂ and 𝑉₂​ are the final pressure and volume under constant temperature conditions.

This derivation succinctly captures Boyle’s Law, emphasizing the inverse proportionality between pressure and volume at constant temperature for an ideal gas.

Uses of Boyles Law

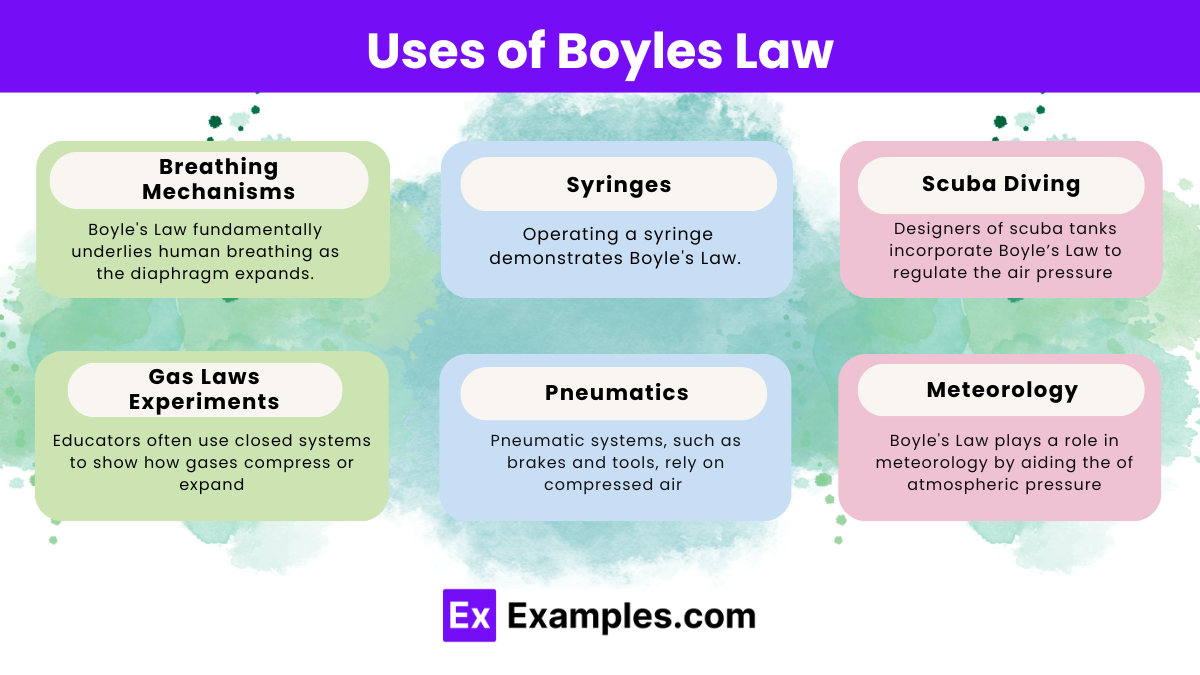
Boyle’s Law describes the inverse relationship between the pressure and volume of a gas at constant temperature and finds application across various fields:

• Breathing Mechanisms: Boyle’s Law fundamentally underlies human breathing. As the diaphragm expands and contracts, it modifies the volume of the lungs, inversely affecting the internal air pressure, enabling the inflow and outflow of air.
• Syringes: Operating a syringe demonstrates Boyle’s Law. Pulling back the plunger increases the internal volume, reducing the pressure and drawing fluid in. Pushing the plunger reduces the volume, increasing the pressure and expelling the fluid.
• Scuba Diving: Designers of scuba tanks incorporate Boyle’s Law to regulate the air pressure provided to divers at varying depths. The pressure increases as a diver goes deeper. Decreasing the volume of air they breathe, which affects the duration a diver can stay underwater with a single tank.
• Gas Laws Experiments: Educators often use closed systems to show how gases compress or expand, helping students learn how gases behave under different pressures and volumes.
• Pneumatics: Pneumatic systems, such as brakes and tools, rely on compressed air and operate on principles derived from Boyle’s Law. Adjusting the air volume and pressure enables these tools to perform mechanical work efficiently.
• Meteorology: Boyle’s Law plays a role in meteorology by aiding the understanding of atmospheric pressure changes crucial for weather prediction and analysis. Changes in atmospheric volume and pressure significantly influence weather patterns.

Examples for Boyles Law

Boyle’s Law plays a vital role across various fields and situations, illustrating the inverse relationship between pressure and volume at constant temperature:

1. Human Breathing: During inhalation, your diaphragm and chest muscles expand the chest cavity, increasing lung volume and decreasing the pressure inside the lungs, allowing air to flow in. During exhalation, the lung volume decreases, the pressure increases, and air flows out.
2. Syringes: Using a syringe demonstrates Boyle’s Law effectively. Pulling back on the syringe plunger increases the volume inside, which decreases the pressure, drawing fluid or air into the syringe.
3. Scuba Diving: Boyle’s Law is crucial for scuba divers. As divers descend deeper underwater, the increased water pressure causes the volume of air in their scuba tanks and lungs to decrease. A key factor in managing breathing and avoiding decompression sickness.
4. Aerosol Cans: The gas in aerosol cans is under high pressure. Pressing the nozzle increases the volume available to the gas as it escapes, decreasing its pressure, which propels the contents out of the can.
5. Car Tires: Boyle’s Law explains why car tires have higher pressure after driving for a while. The air inside the tire warms up from motion and friction. Increasing its pressure if the volume remains constant or increases slightly.
6. Balloons: Balloons inflate because the pressure of the air blown into them exceeds the atmospheric pressure, increasing their volume.

FAQ’s