What does the Saha ionization equation describe?
The temperature of a star
The pressure of a gas
The ionization state of a gas
The velocity of a particle


The Saha Ionization Equation, a fundamental concept in the laws of atomic and molecular physics, quantifies the degree of ionization of gases under equilibrium conditions based on temperature and pressure. It integrates physics principles, including thermodynamics and quantum mechanics, to predict how atoms ionize in stellar atmospheres and other plasmas, illuminating crucial aspects of the laws of physics as they apply to astrophysical phenomena.
The Saha Ionization Equation formula is given by:
Where:
This equation models the ionization balance in astrophysical plasmas and helps in determining the physical conditions of stellar atmospheres.
Understanding the Basic Concept
The Saha Ionization Equation is derived by considering how atoms in a gas can exist in different states—either as neutral atoms or as ionized atoms (atoms missing one or more electrons). The transition between these states involves either the absorption or release of energy, specifically the energy required to remove an electron from an atom.
Applying Thermodynamics
To derive the equation, we start by applying the principles of thermodynamics and statistical mechanics. These principles tell us that the behavior of atoms and electrons in a gas at a given temperature and pressure can be predicted by understanding the distribution of energy among them.
Considering Equilibrium
In a state of thermal equilibrium, the arrangement of electrons and ions in a gas reaches a balance. This balance isn’t static; electrons are continually being knocked out of atoms (ionizing them) and re-captured (re-forming neutral atoms), but the rate of ionization and the rate of recombination are equal, so the overall system remains in equilibrium.
Relating to Energy Levels
The likelihood of an atom being ionized or remaining neutral depends on the energy available to it (from the environment, such as thermal energy at a given temperature) and the energy required to ionize the atom. The higher the temperature, the more thermal energy is available, increasing the likelihood of ionization.
Statistical Considerations
Statistical mechanics provides a framework to calculate the relative populations of neutral and ionized atoms based on their energy states and the temperature of the surrounding environment. It considers all possible energy states of atoms and the statistical likelihood of each state being occupied.
Equating Conditions
The final step in deriving the equation involves setting up an equality condition where the rate at which atoms are ionized equals the rate at which ions recombine into neutral atoms. This involves considering the density of neutral atoms, the density of ions, and the density of free electrons, along with how these quantities change with temperature.
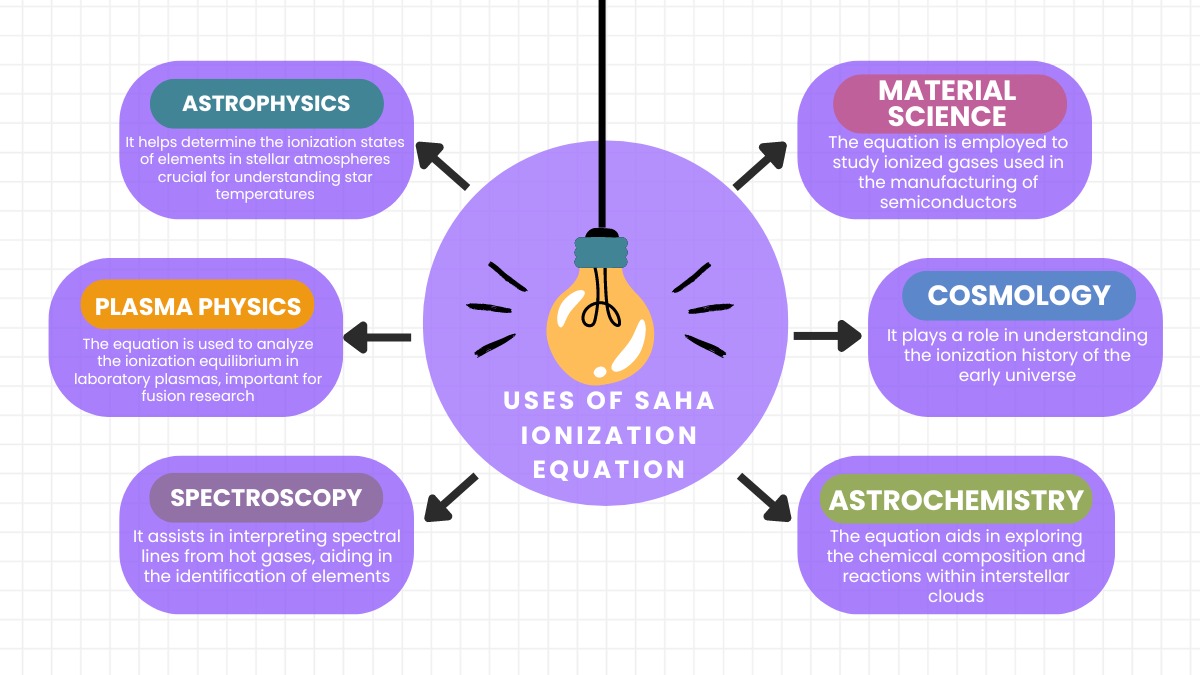
The Saha equation is crucial for determining ionization states in plasmas, essential in astrophysics for analyzing stellar atmospheres and understanding cosmic phenomena.
The Saha-Boltzmann method combines the Saha Ionization Equation and Boltzmann distribution to analyze the thermal and ionization equilibrium in stellar atmospheres, thereby decoding star compositions and temperatures.
Hydrogen begins to ionize at about 10,000 Kelvin, a temperature where enough energy is available to start stripping electrons from hydrogen atoms, significantly seen in stars.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What does the Saha ionization equation describe?
The temperature of a star
The pressure of a gas
The ionization state of a gas
The velocity of a particle
The Saha equation is primarily used in which field of study?
Fluid mechanics
Thermodynamics
Astrophysics
Quantum mechanics
Which fundamental constants are involved in the Saha ionization equation?
Planck constant, Boltzmann constant, and electron charge
Gravitational constant, Boltzmann constant, and speed of light
Planck constant, gravitational constant, and electron charge
Boltzmann constant, speed of light, and Planck constant
What is the primary variable that the Saha equation helps to determine in a stellar atmosphere?
Temperature
Density
Ionization fraction
Pressure
The Saha equation is derived from which two principles of physics?
Newton's laws of motion and thermodynamics
Quantum mechanics and statistical mechanics
Electromagnetism and general relativity
Classical mechanics and fluid dynamics
In the Saha equation, what does nₑ represent?
Number density of electrons
Number density of ions
Energy level of electrons
Temperature of the gas
How does the ionization fraction change with increasing temperature according to the Saha equation?
Decreases
Remains constant
Increases
Varies randomly
What role does the Boltzmann constant (k) play in the Saha ionization equation?
It represents the energy level separation
It sets the scale for thermal energy
It determines the speed of light
It measures the gravitational force
Which of the following conditions is assumed in the derivation of the Saha ionization equation?
Non-equilibrium conditions
Thermal equilibrium
High magnetic field
Low pressure
For hydrogen at a given temperature, what is the effect of increasing pressure on the ionization fraction according to the Saha equation?
Ionization fraction increases
Ionization fraction decreases
Ionization fraction remains constant
Ionization fraction becomes zero
Before you leave, take our quick quiz to enhance your learning!

