Van Der Waals Equation – Examples, Definition, Limitations, FAQ’S

The Van der Waals Equation is an improved model that describes the behavior of real gases, accounting for interactions that the ideal gas law overlooks. It introduces corrections for the finite size of gas molecules and the intermolecular forces between them.

What is Van Der Waals Equation?

Van Der Waals Equation Formula

The formula for the Van der Waals Equation is:

Here’s a breakdown of what each term represents:

• P: The pressure of the gas
• V: The volume of the gas
• n: The number of moles of the gas
• R: The universal gas constant
• T: The absolute temperature of the gas
• a: A constant that accounts for the attractive forces between gas molecules
• b: A constant that corrects for the finite volume occupied by gas molecules

Units of Van der Waals Constants

The units for the Van der Waals constants are:

1. Unit of 𝑎:
   Measures the strength of intermolecular attractive forces.
   Units: atm⋅L²⋅mol⁻²
2. Unit of 𝑏:
   Accounts for the finite volume occupied by gas molecules.
   Units: L⋅mol⁻¹

Van Der Waals Equation Derivation

The Van der Waals Equation modifies the ideal gas law to account for the non-ideal behavior of real gases by considering the volume of gas molecules and the attractive forces between them. Here’s how to derive the Van der Waals Equation:

Ideal Gas Law: Begin with the ideal gas law: 𝑃𝑉=𝑛𝑅𝑇 where:

• P: Pressure
• V: Volume
• n: Number of moles
• R: Universal gas constant
• T: Temperature

Correction for Finite Volume (b): Real gas molecules have a finite size, meaning they occupy some of the container’s volume, reducing the volume available for movement. The volume correction subtracts 𝑛𝑏 from the total volume: 𝑉′=𝑉−𝑛𝑏 where:

• b: Volume occupied by one mole of the gas

• n: Number of moles

Correction for Attractive Forces (a): Real gas molecules attract each other, reducing the impact of collisions with the container walls. This results in a lower pressure than predicted by the ideal gas law. Van der Waals introduced a correction by adding a pressure term: 𝑃′=𝑃+𝑎𝑛²/𝑉²​ where:

• a: Constant that measures the strength of the attractive forces
• n: Number of moles
• V: Volume

This pressure correction reflects the reduction in pressure due to intermolecular attractions.

Combine the Corrections: Substitute the corrected pressure and volume back into the ideal gas law:

(𝑃+𝑎𝑛²/𝑉²)(𝑉−𝑛𝑏)=𝑛𝑅𝑇

This is the Van der Waals Equation, which provides a more accurate description of gas behavior, particularly at high pressures and low temperatures, compared to the ideal gas law.

Van Der Waals Equation of State for Real Gases – Derivation

The Van der Waals equation of state provides a more accurate representation of real gas behavior compared to the ideal gas law. It incorporates corrections for the finite size of gas molecules and the attractive forces between them.

1. Ideal Gas Assumptions:
   The ideal gas law assumes that gas molecules have no volume and do not interact with each other. However, real gases deviate from this ideal behavior, especially at high pressures and low temperatures.
2. Correction for Finite Volume:
   In reality, gas molecules have a finite size and occupy space in the container, which reduces the actual volume available for movement. Van der Waals introduced a correction that accounts for the volume occupied by gas molecules, effectively reducing the available volume for movement.
3. Correction for Attractive Forces:
   Gas molecules exert attractive forces on each other, which lower the effective pressure because the molecules are drawn closer together, reducing the impact of their collisions with the container walls. This attraction correction increases the pressure to account for these intermolecular forces.
4. Modified Equation of State:
   Van der Waals combined these two corrections (finite volume and intermolecular attraction) into a modified version of the ideal gas law. This equation introduces two constants, 𝑎a and 𝑏b, to represent the intermolecular attraction forces and the finite size of gas molecules, respectively.
5. Practical Impact:
   The resulting equation more accurately predicts the behavior of real gases, especially under non-ideal conditions, such as high pressure and low temperature. It helps explain phenomena like gas liquefaction and deviations from ideal gas behavior, leading to better predictions in scientific and industrial applications.

Volume Correction in Van der Waals Equation

In the Van der Waals equation, the volume correction addresses the finite size of gas molecules. In reality, gas molecules occupy a certain amount of space, reducing the effective volume available for gas movement compared to an ideal gas where the molecules are considered point particles with no volume.

Key Aspects of the Volume Correction:

Concept:
The volume occupied by gas molecules themselves cannot be used for free movement. This means that the effective volume available for gas movement is less than the total volume of the container.

Correction Term:
The volume correction is represented by the parameter 𝑏, which accounts for the volume occupied by one mole of gas molecules. The effective volume available for movement is then reduced by subtracting the term 𝑛𝑏, where 𝑛 is the number of moles of gas.

Implication in the Equation:
The Van der Waals equation replaces the volume term of the ideal gas law with a corrected term, reducing the available volume by the amount occupied by gas molecules.

Thus, the volume correction allows the equation to account for the finite size of gas molecules and provides a more accurate representation of real gas behavior than the ideal gas law.

Pressure Correction in Van der Waals Equation

In the Van der Waals equation, the pressure correction accounts for the attractive forces between gas molecules, which are neglected in the ideal gas law. These attractive forces cause gas molecules to experience less effective pressure than would be predicted by the ideal gas law.

Key Aspects of the Pressure Correction:

Concept:
In real gases, molecules attract one another. This attraction reduces the impact that molecules have on the container walls because they tend to cluster together, resulting in a lower effective pressure.

Correction Term:
The pressure correction is represented by the parameter 𝑎, which quantifies the strength of the intermolecular attractive forces. The correction increases the measured pressure to account for this reduced impact due to attraction between molecules.

Implication in the Equation:
The Van der Waals equation includes an additional term to adjust the pressure upward by adding a factor that depends on 𝑎 and the number of moles of gas. This pressure correction helps to more accurately predict the actual pressure of real gases compared to the ideal gas law.

Overall, the pressure correction ensures that the Van der Waals equation reflects the reality of intermolecular attractions and provides a better model of real gas behavior.

Ideal Gas Equation and Van der Waals Equation

The Ideal Gas Equation and the Van der Waals Equation are both equations of state that describe the behavior of gases, though they do so with different assumptions.

Ideal Gas Equation:
The Ideal Gas Equation assumes that gas molecules do not have volume and do not exert attractive or repulsive forces on each other. The equation is expressed as:

𝑃𝑉=𝑛𝑅𝑇

where:

• P: Pressure of the gas
• V: Volume of the gas
• n: Number of moles
• R: Universal gas constant
• T: Temperature of the gas in Kelvin

This equation works well under conditions where gases behave ideally, typically at high temperatures and low pressures.

Van der Waals Equation:
The Van der Waals Equation modifies the Ideal Gas Equation to account for the non-ideal behavior of real gases. It introduces two corrections:

• Volume Correction (b): Gas molecules occupy a finite volume, reducing the space available for free movement. The correction subtracts the term 𝑛𝑏 from the total volume.
• Pressure Correction (a): Attractive forces between gas molecules lower the effective pressure on the container walls. This correction adds a term 𝑎𝑛²/𝑉²​ to account for these intermolecular forces.

The Van der Waals Equation is expressed as:

(𝑃+𝑎𝑛²/𝑉²)(𝑉−𝑛𝑏)=𝑛𝑅𝑇

where:

• a: Measures the strength of intermolecular attractions.
• b: Represents the finite size of gas molecules.

The Van der Waals Equation provides a more accurate model for gas behavior. Especially under high pressure and low temperature conditions where gases deviate significantly from ideal behavior.

Merits of Van der Waals Equation

The Van der Waals equation of state is a more realistic model for describing the behavior of gases compared to the ideal gas law. Here are some of its key merits:

1. Realistic Modeling: It accounts for the non-ideal behavior of real gases by introducing parameters that consider molecular size and intermolecular forces. Offering a more accurate prediction than the ideal gas law.
2. Volume Correction: The equation incorporates the finite size of gas molecules through the volume correction factor (𝑏). Which reduces the available volume for movement and reflects the actual space occupied by gas particles.
3. Pressure Correction: By correcting the pressure with the attraction parameter (𝑎), the equation acknowledges the intermolecular attractions that lower the effective pressure. Particularly at higher densities.
4. Better Predictions: It provides better predictions of gas behavior at high pressures and low temperatures, where deviations from ideal behavior are significant.
5. Applicability to Phase Transitions: The Van der Waals equation can describe phenomena like gas liquefaction and critical points, enabling a better understanding of phase transitions and critical behavior.
6. Foundation for Modern Equations: It forms a basis for more advanced equations of state used in thermodynamics, making it a foundational model in gas theory.
7. Versatility: It can be applied to a wide range of gases. Providing more flexibility and practical utility than simpler models.

Demerits of Van der Waals Equation

While the Van der Waals equation provides a more accurate representation of real gas behavior than the ideal gas law, it still has some limitations:

1. Accuracy Issues: The equation is only an approximation. It may not provide accurate predictions for gases under extreme conditions, particularly at very high pressures or very low temperatures.
2. Empirical Constants: The parameters 𝑎 and 𝑏 are specific to each gas and must be determined experimentally. This reliance on empirical constants makes it less straightforward to apply without prior data.
3. Overestimates Attractive Forces: The parameter 𝑎, which accounts for intermolecular attractions, tends to overestimate the attractive forces between gas molecules, especially near the critical point.
4. Phase Transition Behavior: The equation does not perfectly predict phase transitions, often showing discontinuities that do not match real-world observations, such as during gas-liquid transitions.
5. Complexity: The Van der Waals equation is more complex to use than the ideal gas law, requiring more sophisticated calculations due to its nonlinear nature.
6. Assumptions Remain: Despite improvements over the ideal gas law. It still relies on assumptions, such as uniform particle sizes and forces that are not entirely accurate for all gases.
7. Not Ideal for Multi-Component Systems: The equation has limitations when used to model gas mixtures or multi-component systems, where more sophisticated equations of state are often required.

Uses of Van Der Waals Equation

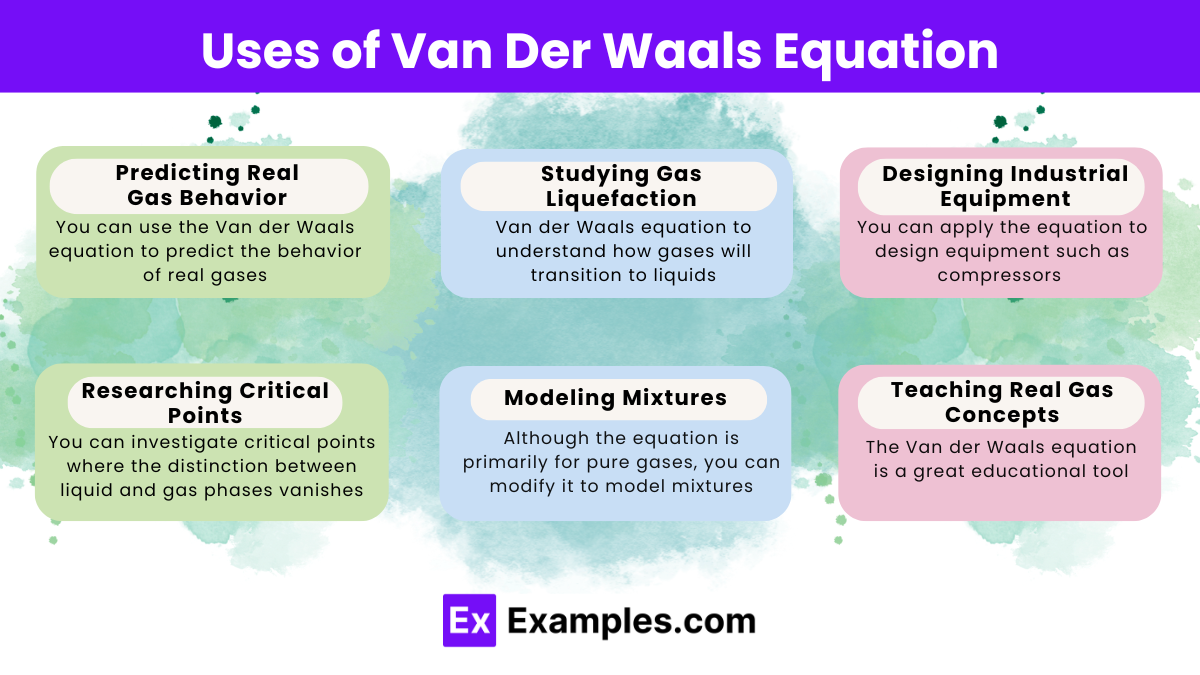
The Van der Waals equation improves upon the ideal gas law by accounting for real gas behavior. Here are some ways you can use this equation:

• Predicting Real Gas Behavior: You can use the Van der Waals equation to predict the behavior of real gases under high pressure or low temperature conditions. This equation provides a more accurate understanding than the ideal gas law.
• Studying Gas Liquefaction: When studying gas liquefaction processes, you can rely on the Van der Waals equation to understand how gases will transition to liquids by analyzing the conditions under which they deviate from ideal behavior.
• Designing Industrial Equipment: You can apply the equation to design equipment such as compressors or gas storage systems. By understanding the behavior of gases. You can better design systems that operate efficiently under non-ideal conditions.
• Researching Critical Points: You can investigate critical points where the distinction between liquid and gas phases vanishes. The Van der Waals equation helps predict this behavior. Which is important in fields like chemical engineering.
• Modeling Mixtures: Although the equation is primarily for pure gases. You can modify it to model mixtures, allowing you to analyze interactions between different gas components.
• Teaching Real Gas Concepts: The Van der Waals equation is a great educational tool. It helps you explain deviations from ideal gas behavior to students. By illustrating how molecular volume and attractive forces impact pressure and volume.

Examples for Van Der Waals Equation

1. Analyzing Phase Changes: For a phase transition like the conversion of water from liquid to ice, the Van der Waals equation can be utilized. By comparing the Van der Waals pressures and volumes of water in its liquid and solid phases at different temperatures. You can predict the temperature at which the phase change occurs in a closed environment.
2. Evaluating Stability in Magnetic Systems: In magnetic systems, such as those involving ferromagnetic materials, the Van der Waals equation can aid in understanding stability. By considering the magnetic field strengths and volumes of different phases, you can calculate the energy differences between various magnetic states and predict which one will be the most stable.
3. Modeling Molecular Systems: In molecular simulations, particularly in closed systems, the Van der Waals equation can be employed to model molecular interactions. By incorporating Van der Waals constants for the molecules involved, you can estimate the relative stability of different molecular conformations by considering their volumes, pressures, and Van der Waals interactions.
4. Designing Thermodynamic Cycles: In the design of thermodynamic cycles for refrigeration or heat pump systems, the Van der Waals equation can be used to optimize efficiency. By evaluating the pressures and volumes of gases in different stages of the cycle, you can maximize the system’s efficiency by minimizing energy losses due to non-ideal behavior.

FAQ’S

What is the Van der Waals Equation?

The Van der Waals Equation of State adjusts the ideal gas law to account for gas molecule size and intermolecular forces.

How does it differ from the ideal gas law?

It incorporates corrections for gas particle volume and attractive forces, providing a more accurate representation of real gas behavior.

When is the Van der Waals Equation used?

It’s applied to describe the behavior of real gases, especially at high pressures or low temperatures, where deviations from ideality are significant.

What are the parameters in the Van der Waals Equation?

The equation includes parameters 𝑎 and 𝑏, representing intermolecular attraction and molecular volume, respectively, for a specific gas.

How does it predict gas behavior at high pressures?

By considering the volume occupied by gas particles and intermolecular attractions, it accurately predicts deviations from ideal gas behavior at high pressures.

Can it be used to describe gas phase transitions?

Yes, it accounts for changes in gas volume and pressure during phase transitions. Such as condensation or liquefaction.

How does it compare to other equations of state?

While it’s more accurate than the ideal gas law. It’s less complex than some equations, striking a balance between simplicity and accuracy.

What’s its significance in thermodynamics?

It aids in understanding real gas behavior. Contributing to the design of processes in chemical engineering, refrigeration, and other fields.

How are the Van der Waals constants determined?

Experimental data, such as critical temperature and pressure, are used to determine the Van der Waals constants for specific gases.

Can it be applied to non-ideal solutions?

Yes, by considering deviations from ideal behavior. The Van der Waals Equation can be adapted to describe non-ideal solutions and mixtures.