What is 144 divided by 12?
12
13
14
15


Division is a fundamental arithmetic operation, closely related to addition, subtraction, and multiplication, forming the cornerstone of basic mathematical education. While addition combines quantities and multiplication scales them, division’s purpose is to distribute a total evenly or to determine how many times one number is contained within another. Subtraction, on the other hand, serves as the inverse process to addition, just as division can be seen as the inverse of multiplication. Mastery of division, along with these other operations, equips learners with the essential skills needed to tackle more complex mathematical concepts and real-world problems efficiently.
Division is a fundamental arithmetic operation where a number, known as the dividend, is evenly distributed into a certain number of smaller, equal parts, each part being the divisor. The outcome of this operation is the quotient, which represents how many times the divisor can be extracted from the dividend.
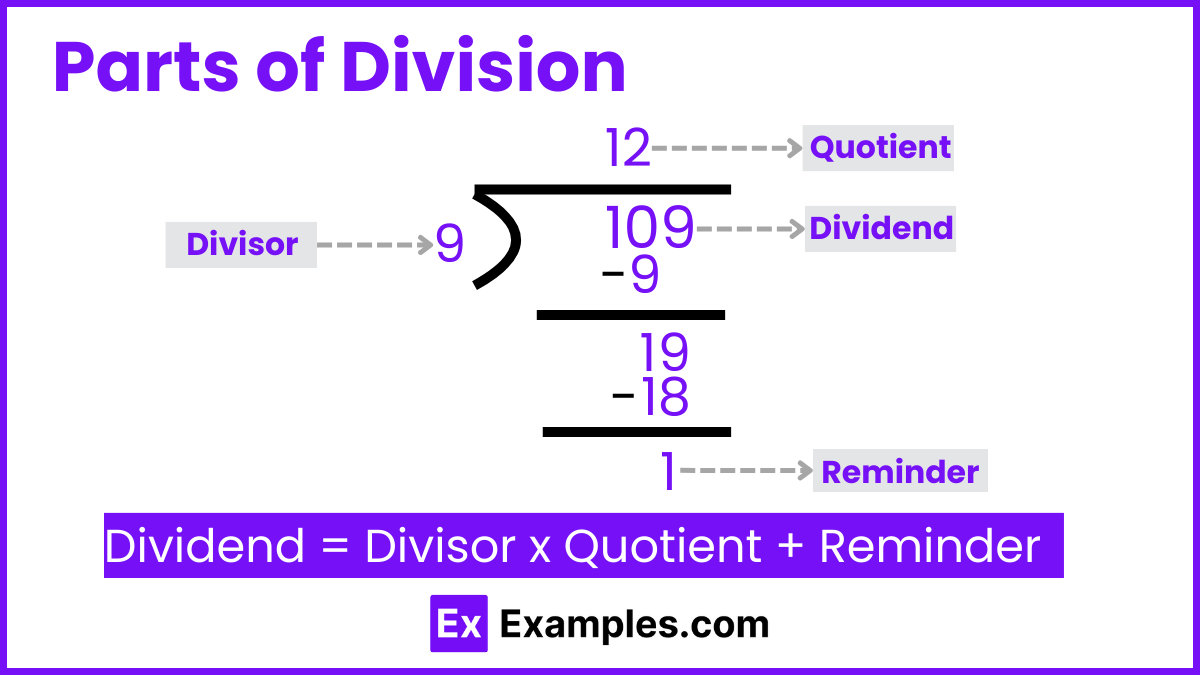
Divisor: This is the number by which the dividend is divided. It represents the number of equal parts or groups into which the dividend is to be split.
Quotient: This is the result of the division. It indicates how many times the divisor fits into the dividend or how many items are in each group.
Remainder: Sometimes, the dividend does not divide evenly by the divisor. The remainder is what is left over after the division is complete. For instance, if you divide 10 by 3, you get a quotient of 3 and a remainder of 1, since 3 groups of 3 make 9, and 1 is left over.
The division operation can be represented using several symbols, each useful in different contexts and for various types of calculations. Here’s a clearer breakdown:
The obelus (÷) is a traditional symbol for division, often used in elementary mathematics and educational settings. This symbol is particularly common when introducing the concept of division to students because it visually represents the operation distinctly.
The slash (/) is commonly used in scientific, programming, and everyday calculations, especially where space is limited or in linear formats. It’s also prevalent in fraction notation, making it versatile for both division and expressing ratios.
The horizontal line, or vinculum, is used primarily in fraction notation and complex expressions of algebra . It’s particularly useful in written work and formal mathematical expressions because it clearly separates the numerator and the denominator, providing a visual clarity that aids in understanding nested operations.

The dividend is the number you want to divide, and the divisor is the number you are dividing by.
Divide the dividend by the divisor to find the quotient. This involves determining how many times the divisor can fit into the dividend.
There are different ways to calculate the quotient:
After subtracting the last multiple of the divisor from the dividend, any number left over is called the remainder.
Let’s divide 125 by 4 using long division:
The process for dividing decimals or fractions involves similar steps but might include additional considerations for placing decimal points or converting fractions to a common denominator.
The Division Algorithm provides a straightforward formula for verifying the results of dividing one integer by another. The relationship expressed by this algorithm encapsulates how division breaks down a larger number (the dividend) into its component parts through multiplication of the divisor and the quotient, and addition of the remainder. The formula you’ve mentioned, Dividend=(Divisor×Quotient)++Remainder, accurately checks and confirms the correctness of the division process.
Here’s a detailed explanation and an example to better illustrate this concept:
The Division Algorithm states that for any integers a (dividend) and b (divisor, where b≠0there exist unique integers q (quotient) and r (remainder) such that:
a=bq+r
and 0≤r<∣b∣
This formula is vital for verifying the results of a division. By plugging in the values of b, q and r, and comparing the calculated result to a, one can confirm whether the division was performed correctly.
Let’s divide 17 by 3.
Now, applying the Division Algorithm: a=bq+r
17=3×5+2
Calculation:
3×5=15
15+2=17
Thus, the equation holds: 17=17
This example demonstrates the algorithm’s practical application. After performing the division, you can use the formula to check your work:
If the values match, as they do in our example, it confirms the division was executed correctly. This check is particularly useful in manual calculations and when teaching the concept of division, as it reinforces understanding of how each part of the division—divisor, quotient, and remainder—interacts to reconstruct the original number. This methodical verification helps ensure accuracy in arithmetic operations and instills confidence in the process.
Dividing any number by 1 leaves it unchanged. This is because the number one is the multiplicative identity, meaning any number multiplied by one is the number itself.
Division by zero is undefined. In mathematics, dividing a number by zero does not produce a finite result, as there is no number that multiplied by zero gives any number other than zero.
When zero is divided by any non-zero number, the quotient is always zero. This is because zero divided into any number of parts is still zero.
Any non-zero number divided by itself equals one, because any number contains exactly one of itself.
Unlike addition and multiplication, division does not have the commutative property. The order in which you divide matters.
Division also lacks the associative property. Changing the grouping of the numbers in a division problem will likely change the result.
Division distributes over addition only under specific circumstances. It’s more common to apply distributive property with multiplication.
2×(4+6)=(2×4)+(2×6).
If we divide a number by 10, then the digit at the ones place will always be the remainder and the remaining digits on the left will be the quotient. For example, 579 ÷ 10 = 57 R 9.
If we divide a number by 100, then the number formed from the ones place and the tens place digits will always be the remainder and the remaining digits on the left will be the quotient. For example, 8709 ÷ 100 = 87 R 9.

Here Reminder is 0.
To enhance comprehension of the division process, we can explore various examples that illustrate different scenarios and challenges typically encountered in division. Each example is designed to highlight specific aspects of the division operation, catering to different levels of difficulty and showcasing unique properties of division. Here’s a refined introduction:
Dividing fractions might seem complex at first, but it follows a straightforward rule known as “multiplication by the reciprocal.” Here’s how you can divide fractions step by step:
The reciprocal of a fraction is obtained by swapping its numerator and denominator. If you have a fraction ba\frac{b}{a}ab, its reciprocal is ab\frac{a}{b}ba.
Turn the division into a multiplication problem by multiplying the dividend by the reciprocal of the divisor.
If possible, simplify the resulting fraction by canceling any common factors between the numerator and the denominator.
Let’s consider an example to illustrate this:
Divide 3/4 by 2/5.
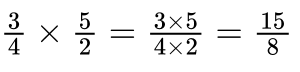
Problem: Divide 56 by 8.
Solution:
56÷8=7
Explanation: 8 goes into 56 exactly 7 times without any remainder.
Problem: Divide 29 by 4.
Solution:
29÷4=7 remainder 1
Explanation: 4 goes into 29 seven times, which accounts for 28 (4 x 7), and there is a remainder of 1.
Problem: Divide 7.2 by 0.6.
Solution:
7.2÷0.6=12
Explanation: 0.6 goes into 7.2 exactly 12 times. A useful strategy here is to eliminate the decimal by multiplying both the dividend and the divisor by 10, transforming it into 72 ÷ 6, which simplifies to 12.
The division allows people to understand the concept of cutting down a specific procedure, product, responsibility, etc. into equal and manageable chunks. This concept allows us to divide specific things and share them with specific people practically. A common real-life example of the application of division is through the division of tasks in specific group work. If the person allocating the task does the dividing properly, each member will have equal amounts of input and responsibility, while dividing up the effort needed to complete said group work. Another real-life example of the practical application of division is observed in the ability to budget and allocate one’s funds for a whole year or month.
The division is a mathematical operation that concerns itself with the cutting or separating of numbers. This operation is the juxtaposition and the inverse of multiplication, similar to the relationship between subtraction and addition. This is an important technique to learn due to its numerous applications in logic and real-life.
Division is an arithmetic operation that determines how many times one number (the divisor) fits into another (the dividend). It essentially splits a larger number into smaller, equal parts.
Division is a core mathematical operation represented by the symbol ➗. It calculates the number of times one number is contained within another, often resulting in a quotient and possibly a remainder.
To type the division symbol ➗ on most keyboards, hold down the Alt key and type 0247 on the numeric keypad, then release the Alt key.
An example of division is 20 divided by 4, which equals 5. Here, 20 is the dividend, 4 is the divisor, and 5 is the quotient.
Explain division to kids as sharing equally. For instance, if 10 cookies are shared among 5 children, each child gets 2 cookies. It’s like breaking a whole into equal parts.
To divide easily, use techniques like long division for larger numbers or mental math for simpler numbers, focusing on multiplication tables to help find the correct quotient quickly.
Start by teaching the concept of sharing equally, using physical objects like counters or blocks. Gradually introduce numbers and symbols, and practice with simple, real-life scenarios.
Solve a division problem by determining how many times the divisor can fit into the dividend. Use long division for complex numbers, breaking it down into manageable steps and subtracting as you go.
Yes, in mathematics, “division” refers to the process of dividing. It involves calculating how many times one number divides into another, which can also be thought of as distributing one number into equal parts of another.

Division is a fundamental arithmetic operation, closely related to addition, subtraction, and multiplication, forming the cornerstone of basic mathematical education. While addition combines quantities and multiplication scales them, division’s purpose is to distribute a total evenly or to determine how many times one number is contained within another. Subtraction, on the other hand, serves as the inverse process to addition, just as division can be seen as the inverse of multiplication. Mastery of division, along with these other operations, equips learners with the essential skills needed to tackle more complex mathematical concepts and real-world problems efficiently.
Division is a fundamental arithmetic operation where a number, known as the dividend, is evenly distributed into a certain number of smaller, equal parts, each part being the divisor. The outcome of this operation is the quotient, which represents how many times the divisor can be extracted from the dividend.

Dividend: This is the number that is being divided. It is the total amount or quantity that you want to distribute or break into smaller parts.
Divisor: This is the number by which the dividend is divided. It represents the number of equal parts or groups into which the dividend is to be split.
Quotient: This is the result of the division. It indicates how many times the divisor fits into the dividend or how many items are in each group.
Remainder: Sometimes, the dividend does not divide evenly by the divisor. The remainder is what is left over after the division is complete. For instance, if you divide 10 by 3, you get a quotient of 3 and a remainder of 1, since 3 groups of 3 make 9, and 1 is left over.
The division operation can be represented using several symbols, each useful in different contexts and for various types of calculations. Here’s a clearer breakdown:
The obelus (÷) is a traditional symbol for division, often used in elementary mathematics and educational settings. This symbol is particularly common when introducing the concept of division to students because it visually represents the operation distinctly.
Example8÷2=4
The slash (/) is commonly used in scientific, programming, and everyday calculations, especially where space is limited or in linear formats. It’s also prevalent in fraction notation, making it versatile for both division and expressing ratios.
Example: 8/2=4
The horizontal line, or vinculum, is used primarily in fraction notation and complex expressions of algebra . It’s particularly useful in written work and formal mathematical expressions because it clearly separates the numerator and the denominator, providing a visual clarity that aids in understanding nested operations.
Mathematical Expression:

Elementary Education: The obelus (÷) is often introduced first to young learners as it clearly differentiates the division operation from others.
Scientific and Technical Work: The slash (/) is favored for its compactness and ease of use in formulas that involve multiple operations and in programming contexts.
Higher Mathematics and Formal Writing: The horizontal line is preferred for its clarity in complex fractions and algebraic expressions where multiple levels of operations are present.
The dividend is the number you want to divide, and the divisor is the number you are dividing by.
Divide the dividend by the divisor to find the quotient. This involves determining how many times the divisor can fit into the dividend.
There are different ways to calculate the quotient:
Long Division: This method is useful for dividing larger numbers. You divide parts of the dividend by the divisor and subtract the largest multiple of the divisor that is less than or equal to that part of the dividend, bringing down the next digit of the dividend when necessary.
Short Division: This is a simpler form of long division suitable for smaller numbers or when the divisor is a single digit.
After subtracting the last multiple of the divisor from the dividend, any number left over is called the remainder.
Let’s divide 125 by 4 using long division:
Write 125 as the dividend and 4 as the divisor.
Determine how many times 4 fits into the first digit (or the first two digits if the first digit is too small). In this case, 4 fits into 12 three times.
Multiply the divisor (4) by the quotient (3) to get 12, and subtract this from the first part of the dividend (12), leaving 0.
Bring down the next digit of the dividend (5), making it 05.
Determine how many times 4 fits into 5, which is 1.
Multiply 4 by 1 to get 4, and subtract this from 5 to get a remainder of 1.
The quotient is 31, and the remainder is 1.
The process for dividing decimals or fractions involves similar steps but might include additional considerations for placing decimal points or converting fractions to a common denominator.
The Division Algorithm provides a straightforward formula for verifying the results of dividing one integer by another. The relationship expressed by this algorithm encapsulates how division breaks down a larger number (the dividend) into its component parts through multiplication of the divisor and the quotient, and addition of the remainder. The formula you’ve mentioned, Dividend=(Divisor×Quotient)++Remainder, accurately checks and confirms the correctness of the division process.
Here’s a detailed explanation and an example to better illustrate this concept:
The Division Algorithm states that for any integers a (dividend) and b (divisor, where b≠0there exist unique integers q (quotient) and r (remainder) such that:
a=bq+r
and 0≤r<∣b∣
This formula is vital for verifying the results of a division. By plugging in the values of b, q and r, and comparing the calculated result to a, one can confirm whether the division was performed correctly.
Let’s divide 17 by 3.
Dividend a: 17
Divisor b: 3
The division gives us a quotient q of 5 and a remainder r of 2.
Now, applying the Division Algorithm: a=bq+r
17=3×5+2
Calculation:
3×5=15
15+2=17
Thus, the equation holds: 17=17
This example demonstrates the algorithm’s practical application. After performing the division, you can use the formula to check your work:
Multiply the divisor by the quotient.
Add the remainder to the product from step 1.
Compare the result with the original dividend.
If the values match, as they do in our example, it confirms the division was executed correctly. This check is particularly useful in manual calculations and when teaching the concept of division, as it reinforces understanding of how each part of the division—divisor, quotient, and remainder—interacts to reconstruct the original number. This methodical verification helps ensure accuracy in arithmetic operations and instills confidence in the process.
Dividing any number by 1 leaves it unchanged. This is because the number one is the multiplicative identity, meaning any number multiplied by one is the number itself.
Example: 25÷1=25
Division by zero is undefined. In mathematics, dividing a number by zero does not produce a finite result, as there is no number that multiplied by zero gives any number other than zero.
Example: 25÷0 is undefined.
When zero is divided by any non-zero number, the quotient is always zero. This is because zero divided into any number of parts is still zero.
Example: 0÷5=0
Any non-zero number divided by itself equals one, because any number contains exactly one of itself.
Example: 19÷9=1
Unlike addition and multiplication, division does not have the commutative property. The order in which you divide matters.
Example: 12÷4=3, but 4÷12=1/3
Division also lacks the associative property. Changing the grouping of the numbers in a division problem will likely change the result.
Example: (24÷3)÷2=4, but 24÷(3÷2)=16
Division distributes over addition only under specific circumstances. It’s more common to apply distributive property with multiplication.
Example: Distributive property is not typically used to simplify expressions where division distributes over addition. However, multiplication related to division shows distributive property like
2×(4+6)=(2×4)+(2×6).
If we divide a number by 10, then the digit at the ones place will always be the remainder and the remaining digits on the left will be the quotient. For example, 579 ÷ 10 = 57 R 9.
If we divide a number by 100, then the number formed from the ones place and the tens place digits will always be the remainder and the remaining digits on the left will be the quotient. For example, 8709 ÷ 100 = 87 R 9.

Here Reminder is 0.
To enhance comprehension of the division process, we can explore various examples that illustrate different scenarios and challenges typically encountered in division. Each example is designed to highlight specific aspects of the division operation, catering to different levels of difficulty and showcasing unique properties of division. Here’s a refined introduction:
Dividing fractions might seem complex at first, but it follows a straightforward rule known as “multiplication by the reciprocal.” Here’s how you can divide fractions step by step:
Dividend: This is the fraction that you are dividing.
Divisor: This is the fraction by which you are dividing.
The reciprocal of a fraction is obtained by swapping its numerator and denominator. If you have a fraction ba\frac{b}{a}ab, its reciprocal is ab\frac{a}{b}ba.
Turn the division into a multiplication problem by multiplying the dividend by the reciprocal of the divisor.
If possible, simplify the resulting fraction by canceling any common factors between the numerator and the denominator.
Let’s consider an example to illustrate this:
Divide 3/4 by 2/5.
Dividend: 3/4
Divisor: 2/5
Reciprocal of the Divisor: The reciprocal of 2/5 is 5/2.
Multiply: Multiply the dividend by the reciprocal of the divisor
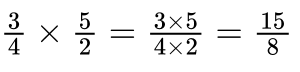
Simplify: The result 15/8 is already in its simplest form.
Problem: Divide 56 by 8.
Solution:
56÷8=7
Explanation: 8 goes into 56 exactly 7 times without any remainder.
Problem: Divide 29 by 4.
Solution:
29÷4=7 remainder 1
Explanation: 4 goes into 29 seven times, which accounts for 28 (4 x 7), and there is a remainder of 1.
Problem: Divide 7.2 by 0.6.
Solution:
7.2÷0.6=12
Explanation: 0.6 goes into 7.2 exactly 12 times. A useful strategy here is to eliminate the decimal by multiplying both the dividend and the divisor by 10, transforming it into 72 ÷ 6, which simplifies to 12.

benning.army.mil

uhcl.edu

aspet.org

iosrjen.org

cdn.ymaws.com

aseecmsduq.blob.core.windows.net
wgps.vic.edu.au

info.belden.com

eworkshop.on.ca

digitalcommons.kean.edu

mass.gov
scdhec.gov

edu.gov.mb.ca

16thcircuit.org

scchildcare.org

anu.edu.au
usu.edu

rheumatology.org

cookman.edu

it.wisc.edu
When you have finished multiplying the fractions, you will then simplify the fractions to their simplest form. This means that you must check if both the dividend and divisor share a denominator. Using the example both 4 and 18 have an LCD of 2, allowing you to simplify the example to 2/9.
Synthetic division is a technique people use to divide polynomial equations. These equations are quite daunting to look at and are harder to divide when compared to other types of equations. Synthetic division is a short-hand technique that allows the person to divide polynomial equations with more ease when compared to the longer and more nuanced technique. This is because synthetic division presents a more simplified and less complicated look when compared to the long polynomial division method, which is achieved by taking out X or any of the variables in the equation and writing the numbers attached to them instead
Long division refers to the simple technique of dividing numbers through the divisor and the dividend. Common examples of equations that utilize long division are x/y, quotient between x and y, and x divided by y where x is the dividend and y is the divisor. This is characterized by the use of the long division symbol (?) and with the dividend on the left side while the divisor is sequestered on the right side of the symbol. This is often the go-to method in dividing numbers with high values and is often accompanied by a simplification process (through the usage of the Least Common Denominator or LCD) to help ease up the difficulty of the long division.
The division allows people to understand the concept of cutting down a specific procedure, product, responsibility, etc. into equal and manageable chunks. This concept allows us to divide specific things and share them with specific people practically. A common real-life example of the application of division is through the division of tasks in specific group work. If the person allocating the task does the dividing properly, each member will have equal amounts of input and responsibility, while dividing up the effort needed to complete said group work. Another real-life example of the practical application of division is observed in the ability to budget and allocate one’s funds for a whole year or month.
The division is a mathematical operation that concerns itself with the cutting or separating of numbers. This operation is the juxtaposition and the inverse of multiplication, similar to the relationship between subtraction and addition. This is an important technique to learn due to its numerous applications in logic and real-life.
Division is an arithmetic operation that determines how many times one number (the divisor) fits into another (the dividend). It essentially splits a larger number into smaller, equal parts.
Division is a core mathematical operation represented by the symbol ➗. It calculates the number of times one number is contained within another, often resulting in a quotient and possibly a remainder.
To type the division symbol ➗ on most keyboards, hold down the Alt key and type 0247 on the numeric keypad, then release the Alt key.
An example of division is 20 divided by 4, which equals 5. Here, 20 is the dividend, 4 is the divisor, and 5 is the quotient.
Explain division to kids as sharing equally. For instance, if 10 cookies are shared among 5 children, each child gets 2 cookies. It’s like breaking a whole into equal parts.
To divide easily, use techniques like long division for larger numbers or mental math for simpler numbers, focusing on multiplication tables to help find the correct quotient quickly.
Start by teaching the concept of sharing equally, using physical objects like counters or blocks. Gradually introduce numbers and symbols, and practice with simple, real-life scenarios.
Solve a division problem by determining how many times the divisor can fit into the dividend. Use long division for complex numbers, breaking it down into manageable steps and subtracting as you go.
Yes, in mathematics, “division” refers to the process of dividing. It involves calculating how many times one number divides into another, which can also be thought of as distributing one number into equal parts of another.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is 144 divided by 12?
12
13
14
15
What is the result of 96 divided by 8?
10
11
12
13
If you divide 81 by 9, what do you get?
7
8
9
10
What is 120 divided by 15?
6
7
8
9
Divide 75 by 5. What is the result?
14
15
16
17
What is the quotient when 200 is divided by 20?
8
9
10
11
What is 180 divided by 6?
28
29
30
31
If you divide 240 by 30, what do you get?
6
7
8
9
What is 90 divided by 10?
8
9
10
11
What is the result of dividing 250 by 25?
8
9
10
11
Before you leave, take our quick quiz to enhance your learning!

