Expressions

What are Expressions?

Expressions in mathematics are combinations of numbers, variables (letters that represent unknown values), and operations (such as addition, subtraction, multiplication, and division) that represent a particular value. Unlike equations, expressions do not have an equal sign. They are used to convey a mathematical idea or quantity without explicitly stating an equality.

Components of Mathematical Expressions

Mathematical expressions are fundamental constructs in algebra that consist of terms joined by mathematical operations like addition, subtraction, multiplication, and division. Here’s a breakdown of the critical elements that make up mathematical expressions:

1. Constants

• Definition: Constants are fixed values that do not change. They are specific numbers included in the expression to define the mathematical relationships.
• Example: In the expression 3𝑥+5, the number 5 is a constant.

2. Variables

• Definition: Variables are symbols, typically letters, that represent unknown or variable quantities. They can change depending on the context or conditions of the problem.
• Example: In 3𝑥+5, 𝑥 is a variable that can take various numerical values.

3. Terms

• Definition: A term is a component of an expression that can be a constant, a variable, or a combination of both connected by multiplication or division.
• Example: 3𝑥 and 5are both terms in the expression 3𝑥+5.

4. Coefficients

• Definition: A coefficient is a number used to multiply a variable within an expression. It quantifies the variable.
• Example: In 3𝑥, the coefficient is 3, indicating that 𝑥 is multiplied by 3.

Expression in Math Example

Types of Expressions in Math

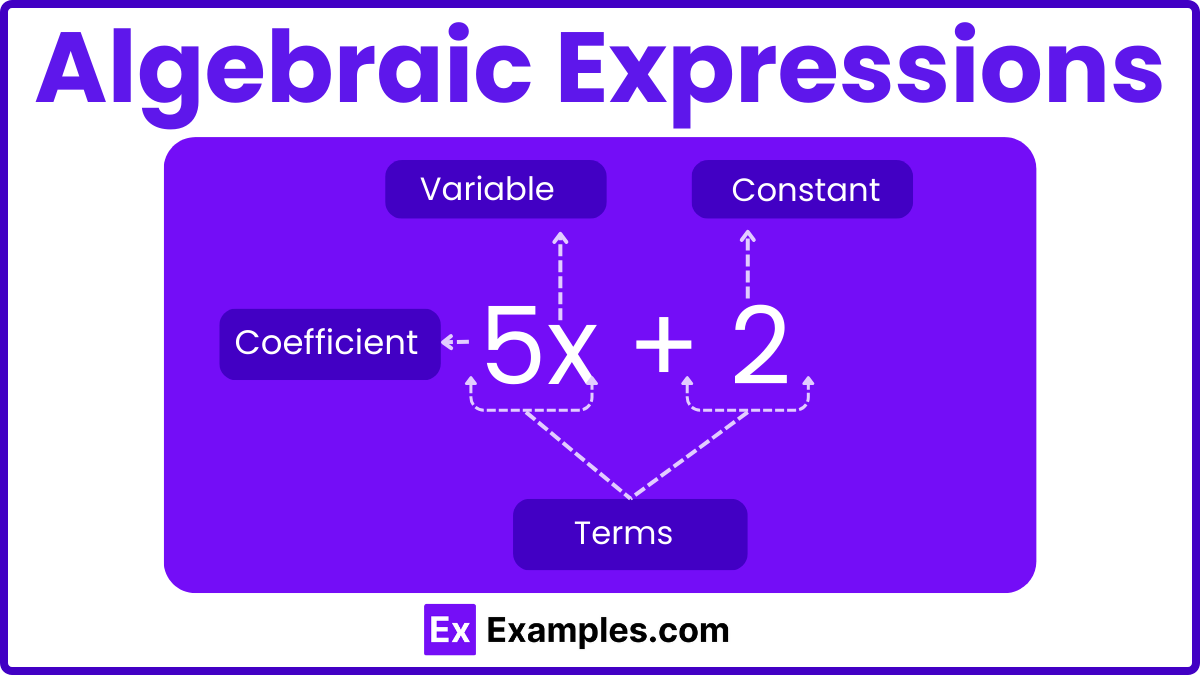
Mathematical expressions can be broadly categorized into three types based on the terms they include. Each type plays a crucial role in various mathematical calculations and problem-solving scenarios. Below, we’ll delve into each category, explaining their distinct characteristics and functions.

Type of Expression	Definition	Example
Arithmetic Expressions	Consist solely of numbers and operation symbols, without any variables.	7+4×2
Fractional Expressions	Include numerators and denominators that are algebraic expressions.	2𝑥+3/𝑥−5
Algebraic Expressions	Contain variables, constants, and arithmetic operations, and can vary in complexity.	3𝑥²−2𝑥+5

1. Arithmetic or Numerical Expressions

• Definition: These expressions consist solely of numbers and operation symbols. They do not contain any variables.
• Function: Arithmetic expressions are used for basic calculations and are fundamental in everyday math.
• Example: An expression like 7+4×2 is arithmetic because it only involves numbers and operations.

2. Fractional Expressions

• Definition: Fractional expressions include numerators and denominators that are algebraic expressions.
• Function: These are essential for operations involving ratios and proportions in more advanced mathematical contexts, such as solving for variables in equations.
• Example: The expression (2𝑥+3)/(𝑥−5​) is fractional, with algebraic expressions in both the numerator and the denominator.

3. Algebraic Expressions

• Definition: Algebraic expressions contain variables, constants, and arithmetic operations. They can vary significantly in complexity.
• Function: Algebraic expressions are used extensively in algebra to represent relationships, formulate equations, and solve problems.
• Example: 3𝑥²−2𝑥+5 is an algebraic expression featuring variables (x), coefficients (3 and -2), and a constant (5).

Algebraic expressions, particularly focusing on polynomials, which are divided based on the number of terms they contain. This classification includes monomials, binomials, trinomials, and general polynomials, providing clear definitions and examples for each:

Type of Algebraic Expression	Definition	Example
Monomial	An expression with only one term, consisting of a coefficient and a variable raised to a power.	5𝑥3
Binomial	An expression that consists of two terms, which are not like terms.	3𝑥²−2𝑥
Trinomial	An expression made up of three terms, which are not like terms.	𝑥²−4𝑥+4
Polynomial	A more general category that includes expressions with one or more terms (including monomial and above).	4𝑥³−3𝑥²+2𝑥−1

Expression vs Equation

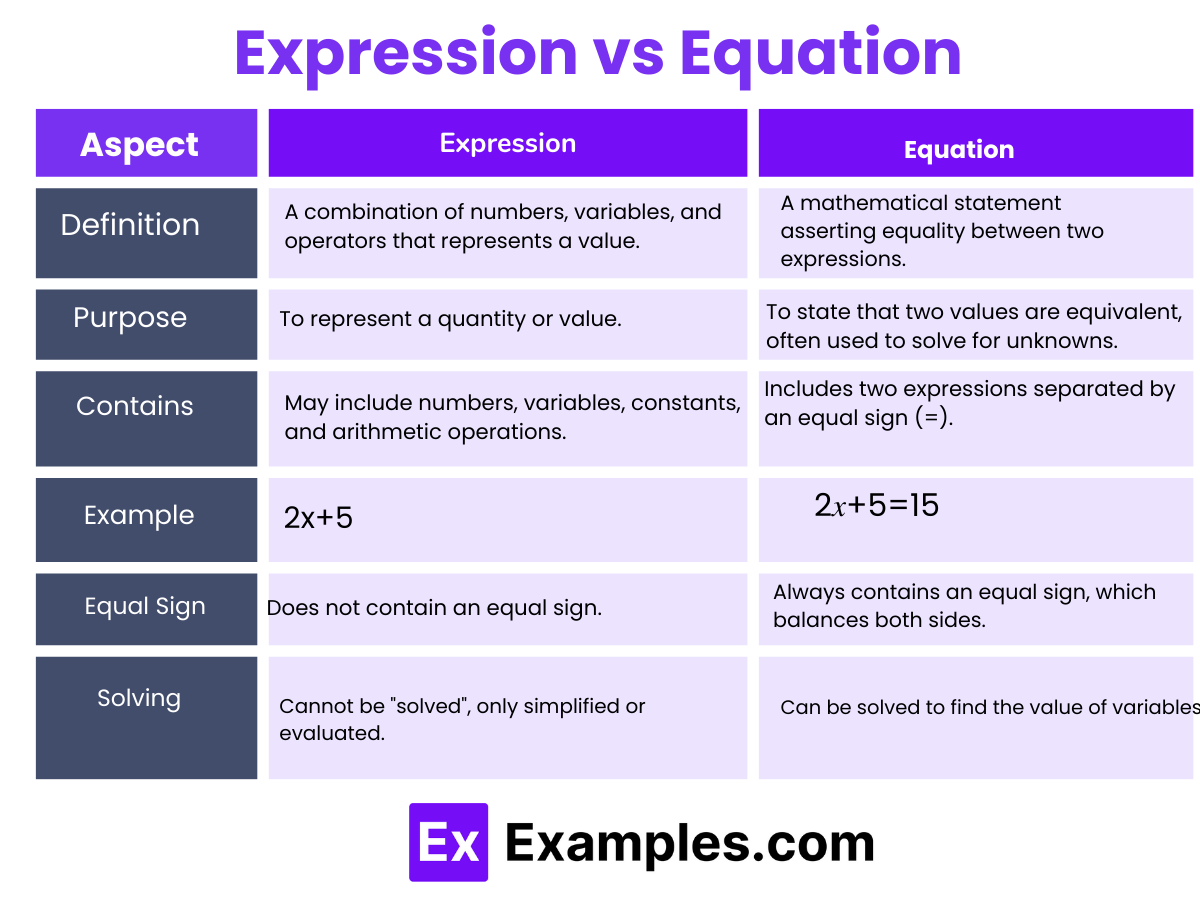
Aspect	Expression	Equation
Definition	A combination of numbers, variables, and operators that represents a value.	A mathematical statement asserting equality between two expressions.
Contains	May include numbers, variables, constants, and arithmetic operations.	Includes two expressions separated by an equal sign (=).
Purpose	To represent a quantity or value.	To state that two values are equivalent, often used to solve for unknowns.
Example	2𝑥+5	2𝑥+5=15
Equal Sign	Does not contain an equal sign.	Always contains an equal sign, which balances both sides.
Solving	Cannot be “solved”, only simplified or evaluated.	Can be solved to find the value of variables.

Simplifying Expressions in Mathematics

Simplifying mathematical expressions is a fundamental skill in algebra that helps make complex problems more manageable and solutions clearer. Here are step-by-step guidelines and tips for effectively simplifying expressions:

1. Combine Like Terms

• Definition: Like terms are terms that have the same variable raised to the same power.
• Process: Add or subtract coefficients of like terms.
• Example: Simplify 3𝑥+5𝑥 to 8𝑥

2. Use the Distributive Property

• Property: The distributive property states that 𝑎(𝑏+𝑐)=𝑎𝑏+𝑎𝑐a(b+c)=ab+ac.
• Application: Use this property to eliminate parentheses in expressions.
• Example: Simplify 2(3𝑥+4) to 6𝑥+8

3. Apply the Associative and Commutative Properties

• Associative Property: Changing the grouping of the numbers does not change the sum or product (e.g., (𝑎+𝑏)+𝑐=𝑎+(𝑏+𝑐)
• Commutative Property: Changing the order of the numbers does not change the sum or product (e.g., 𝑎+𝑏=𝑏+𝑎);
• Use: These properties can be used to rearrange and group terms for easier combination.

4. Simplify Fractions within Expressions

• Fraction Simplification: Reduce fractions to their simplest form.
• Example: In the expression 6𝑥/9​, simplify the fraction to 2𝑥/3​.

5. Factor Out Common Factors

• Factoring: Identify and factor out the greatest common factor from terms.
• Example: For the expression 12𝑥²+18𝑥, factor out 6𝑥 to get 6𝑥(2𝑥+3).

6. Clear Decimals or Complex Numbers

• Clearing Decimals: Multiply through by powers of 10 to eliminate decimals.
• Example: To simplify 0.2𝑥+0.5, multiply every term by 10 to get 2𝑥+5.

7. Use Algebraic Identities

• Identities: Apply identities like 𝑎²−𝑏²=(𝑎+𝑏)(𝑎−𝑏) to simplify expressions.
• Example: Simplify x²−9 to (𝑥+3)(𝑥−3).

Practice probleams with Answers

1. Simplify the Expression

Problem: Simplify the expression 4𝑥+3𝑥−2+6

Solution: Combine like terms.

• 4𝑥+3𝑥=7𝑥
• −2+6=4

So, 4𝑥+3𝑥−2+6 simplifies to 7𝑥+4

Problem 2: Identify Parts of the Expression

Problem: Identify the coefficients and the constant in the expression 5𝑦²−3𝑦+7

Solution:

• Coefficients are 5 and -3.
• The constant is 7.

Problem 3: Using the Distributive Property

Problem: Simplify the expression 3(2𝑥+4)) using the distributive property.

Solution: Apply the distributive property:

• 3⋅2𝑥=6𝑥
• 3⋅4=12

So, 3(2𝑥+4) simplifies to 6𝑥+12

Problem 4: Factor Out the Greatest Common Factor

Problem: Factor out the greatest common factor from the expression 18𝑥²+9𝑥

Solution: Identify the greatest common factor:

• The greatest common factor of 18 and 9 is 9.
• The lowest power of 𝑥 common to both terms is 𝑥.

So, the greatest common factor is 9x, and 18𝑥²+9x factors to 9𝑥(2𝑥+1)

FAQs

What is Expressions and Formulae?

Expressions are combinations of variables and constants using mathematical operations. Formulae are specific types of expressions that algebraically represent relationships between different variables.

What are the 4 Types of Expression?

The four main types of expressions are arithmetic (involving only numbers and operations), algebraic (including variables and constants), polynomial (a type of algebraic expression with multiple terms), and rational (involving ratios of polynomials).

How to Write Math Expressions?

Writing math expressions involves using symbols and notation to represent numbers, operations, and relationships. Ensure clarity by correctly using parentheses to dictate the order of operations.

How to Teach Expressions in Math?

Teach mathematical expressions by starting with basic arithmetic expressions, introducing variables for unknowns, and progressing to more complex algebraic forms. Use examples and practical problems for better understanding.