Geometric Progression

What is Geometric Progression?

Geometric Progression (GP), also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio (r).

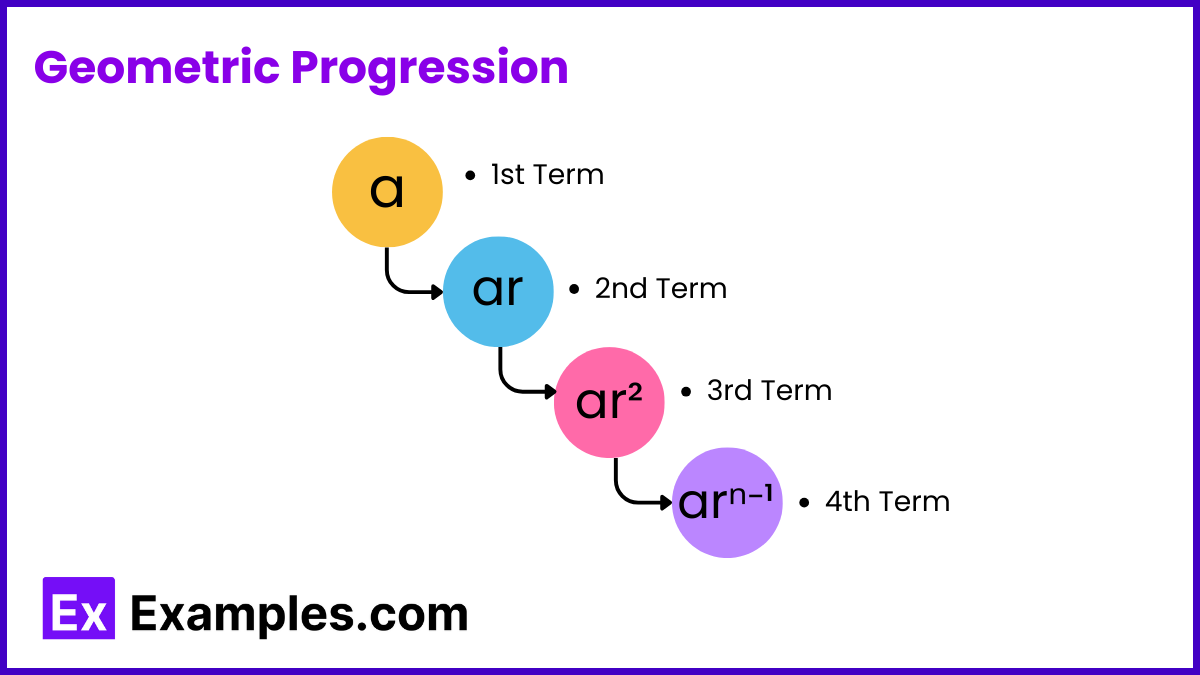
Geometric Progression (GP) is a sequence where each term is found by multiplying the previous one by a fixed number, known as the common ratio. It’s symbolized as ‘a, ar, ar²…’ where ‘a’ is the first term and ‘r’ is the common ratio. ‘r’ can be positive or negative. With just the first term and the ratio, you can determine all the terms of the sequence.

Geometric Progression Formula

Here are the formulas related to geometric progressions, considering a sequence that begins with 𝑎a and follows the pattern a, ar, ar²,𝑎𝑟³….

• nᵗʰ  term: a_n = arⁿ⁻¹ (or) aₙ = r aₙ₋₁
• Sum of the first n terms: Sₙ = a(rⁿ – 1) / (r – 1) when r ≠ 1 and Sₙ = na when r = 1.
• Sum of infinite terms: S_∞ = a / (1 – r) when |r| < 1 and the sum is NOT defined when |r| ≥ 1.

Properties of Geometric Progression (GP)

Here are the important properties of Geometric Progression (GP) presented more succinctly:

1. Geometric Mean Property: For three non-zero terms a, b, c in GP, 𝑏²=𝑎𝑐.
2. Consecutive Terms: In a GP, three consecutive terms are 𝑎/𝑟a/r, 𝑎a, 𝑎𝑟ar. Four consecutive terms are 𝑎/𝑟³, 𝑎/𝑟, ar, 𝑎𝑟³. Similarly for five consecutive terms.
3. Product of Equidistant Terms: In a finite GP, the product of terms equidistant from the beginning and the end is the same. For instance, 𝑡₁⋅𝑡ₙ=𝑡₂⋅𝑡ₙ₋₁=𝑡₃⋅𝑡ₙ₋₂=…
4. Scaling: If each term of a GP is multiplied or divided by a non-zero constant, the resulting sequence remains a GP with the same common ratio.
5. Product and Quotient: The product and quotient of two GPs are again GPs.
6. Exponentiation: Raising each term of a GP to the power by the same non-zero quantity results in another GP.
7. Relation to Arithmetic Progression (AP): If a GP has positive terms, then the logarithms of its terms form an Arithmetic Progression (AP), and vice versa.

General Form of Geometric Progression

he general form of a Geometric Progression (GP) is represented as:

𝑎,𝑎𝑟,𝑎𝑟²,𝑎𝑟³,𝑎𝑟⁴,…,𝑎𝑟ⁿ⁻¹

Where:

• 𝑎 is the first term of the sequence.
• 𝑟 is the common ratio between consecutive terms.
• 𝑎𝑟ⁿ⁻¹ is the 𝑛𝑡ℎnth term of the sequence.

This formula encapsulates the pattern where each term is obtained by multiplying the previous term by the common ratio ‘r’.

General Term or nth Term of Geometric Progression

Let a be the first term and r be the common ratio for a Geometric Sequence.

Then, the second term, a₂ = a × r = ar

Third term, a₃ = a₂ × r = ar × r = ar²

Similarly, nth term, aₙ = arⁿ⁻¹

Therefore, the formula to find the nth term of GP is:

aₙ = tₙ = arⁿ⁻¹

Common Ratio of GP

Consider the sequence a, ar, ar², ar³,……

First term = a

Second term = ar

Third term = ar²

Similarly, nth term, tₙ = arⁿ⁻¹

Thus, the common ratio of geometric progression formula is given as:

Common ratio = (Any term) / (Preceding term)

= tₙ / tₙ₋₁

= (arⁿ⁻¹ ) /(arⁿ⁻²)

= r

Thus, the general term of a GP is given by ar and the general form of a GP is a, ar, ar²,…..

For Example: r = t₂ / t₁ = ar / a = r

Sum of N term of GP

uppose a, ar, ar², ar³,……arⁿ⁻¹ is the given Geometric Progression.

Then the sum of n terms of GP is given by:

S_n = a + ar + ar^² + ar³ +…+ arⁿ⁻¹

The formula to find the sum of n terms of GP is:

Sₙ = a[(rⁿ – 1)/(r – 1)] if r ≠ 1 and r > 1

Where

a is the first term

r is the common ratio

n is the number of terms

Also, if the common ratio is equal to 1, then the sum of the GP is given by:

Sₙ = na if r = 1

Geometric Progression vs Arithmetic Progression

Aspect	Geometric Progression (GP)	Arithmetic Progression (AP)
Definition	A sequence where each term after the first is multiplied by a constant.	A sequence where each term after the first is added by a constant.
Common Term	Common Ratio (r)	Common Difference (d)
Formula	The nth term is given by 𝑎⋅𝑟(𝑛−1)	The nth term is given by 𝑎+(𝑛−1)⋅𝑑
Example	2, 6, 18, 54, … (where 𝑟=3)	5, 8, 11, 14, … (where 𝑑=3)
Sum Formula	Sum of first n terms: 𝑆ₙ=𝑎⋅𝑟ⁿ⁻¹/𝑟−1(if 𝑟≠1)	Sum of first n terms: 𝑆ₙ=𝑛/2⋅(2𝑎+(𝑛−1)⋅𝑑)
Applications	Used in scenarios involving exponential growth or decay, such as populations, finance.	Used in evenly spaced contexts like scheduling, constructing sequences.

Types of Geometric Progression

1. Finite Geometric Progression (Finite GP):
   • Explanation: A finite GP has a limited number of terms, after which the sequence ends.
   • Representation: 𝑎,𝑎𝑟,ar²,𝑎𝑟³,…,𝑎𝑟ⁿ⁻¹ where 𝑛n is the number of terms.
   • Formula to Find Sum: The sum of a finite GP can be calculated using the formula: 𝑆𝑛=𝑎𝑟ⁿ⁻¹/𝑟−1Where 𝑆𝑛​ is the sum of the first 𝑛 terms, 𝑎a is the first term, 𝑟 is the common ratio, and 𝑛n is the number of terms.
2. Infinite Geometric Progression (Infinite GP):
   • Explanation: An infinite GP continues indefinitely, with no predetermined end.
   • Representation: 𝑎,𝑎𝑟,ar²,𝑎𝑟³,… where the terms continue indefinitely.
   • Formula to Find Sum: The sum of an infinite GP can be calculated using the formula: 𝑆=𝑎/1−𝑟 Where S is the sum of the infinite series, a is the first term, and r is the common ratio (provided ∣𝑟∣<1).

FAQs

Finite Geometric Progression

The terms of a finite G.P. can be written as a, ar, ar², ar³,……arⁿ⁻¹

a, ar, ar², ar³,……arⁿ⁻¹ is called finite geometric series.

The sum of finite Geometric series is given by:

Sn = a[(rⁿ – 1)/(r – 1)] if r ≠ 1 and r > 1

Tips for Understanding and Working with Geometric Progressions

Geometric progressions (GPs) are a fundamental concept in mathematics with extensive applications across various fields such as finance, physics, and computer science. Here are some essential tips to help you understand and effectively work with geometric progressions:

1. Understand the Components:
   • Initial Term (a): The first term in the progression.
   • Common Ratio (r): The factor by which each term is multiplied to get the next term. The value of 𝑟r can dramatically change the behavior of the progression, from rapid growth to rapid decay.
2. Visualize the Progression:
   • Graphing the terms of a geometric progression can provide insight into its growth pattern—whether it’s an exponential growth, decay, or constant series.
3. Check for Common Pitfalls:
   • Be cautious with negative values of r, as they cause the terms to alternate between positive and negative.
   • Extremely high or low values of r can lead to terms that grow or shrink very rapidly, making calculations cumbersome or leading to numerical inaccuracies.
4. Application in Real-World Problems:
   • Finance: Use GPs to model investments compounded over time or to calculate the future value of annuities.
   • Physics: Understand phenomena that involve exponential growth or decay, like radioactive decay or population growth under ideal conditions.
5. Practice Different Problems:
   • Work on various exercises involving different values of 𝑎a and r to build intuition and skill in recognizing patterns and solving problems efficiently.
6. Use Technology When Necessary:
   • For complex calculations, especially those involving large exponents or sums of many terms, don’t hesitate to use a scientific calculator or computer software to ensure accuracy.
7. Connect with Other Mathematical Concepts:
   • Relate geometric progressions to sequences, series, and other functions to deepen understanding and broaden application scope.

Four Terms of Geometric Progression

The four terms of a geometric progression are 𝑎,𝑎𝑟,𝑎𝑟2,𝑎𝑟3, where a is the first term and r is the common ratio. Each term is obtained by multiplying the previous term by r.

Rule of Geometric Progression

The rule of geometric progression states that each term in the sequence is obtained by multiplying the previous term by a constant factor, known as the common ratio (𝑟r).

Real-Life Example of Geometric Progression

An example of geometric progression in real life is the growth of a population of bacteria. If each bacterium doubles every hour, the population follows a geometric progression, with the number of bacteria doubling with each generation.

Five Examples of Geometry in Real Life

1. Architecture: Designing buildings and structures using geometric principles.
2. Engineering: Calculating angles and dimensions for bridges and machines.
3. Art: Creating visually appealing compositions using geometric shapes.
4. Navigation: Using geometric concepts to plot routes and determine distances.
5. Sports: Applying geometry in activities like soccer, basketball, and swimming for strategy and technique.