Vector Algebra

What is Vector Algebra?

Vector algebra is a branch of mathematics that deals with vectors, which are quantities having both magnitude and direction. It involves operations such as vector addition, subtraction, scalar multiplication, and the dot and cross products, used extensively in physics and engineering.

Types of Vectors – Vector Algebra

Zero Vector: A vector with zero magnitude and no specific direction.

Unit Vector: A vector with a magnitude of one, indicating direction.

Position Vector: A vector representing the position of a point relative to an origin.

Co-Initial Vectors: Vectors sharing the same initial point.

Collinear Vectors: Vectors that lie along the same line, regardless of magnitude and direction.

Equal Vectors: Vectors with the same magnitude and direction, regardless of their initial points.

Negative Vectors: Vectors with the same magnitude but opposite direction.

Parallel Vectors: Vectors that are parallel to each other, regardless of magnitude.

Vector Algebra Operations

In vector algebra, several basic operations can be performed geometrically without relying on a coordinate system. These operations include vector addition, subtraction, and scalar multiplication. Additionally, vectors can be multiplied in two distinct ways: the dot product and the cross product. These fundamental operations are essential for understanding and manipulating vectors in various applications.

• Addition of Vectors
• Subtraction of Vectors
• Scalar Multiplication
• Scalar Triple Product of Vectors
• Multiplication of Vectors

Vector Addition:

Combining two vectors to form a resultant vector by adding their corresponding components.

• Example: If A = (a1, a2) and B = (b1, b2), then A + B = (a1 + b1, a2 + b2).

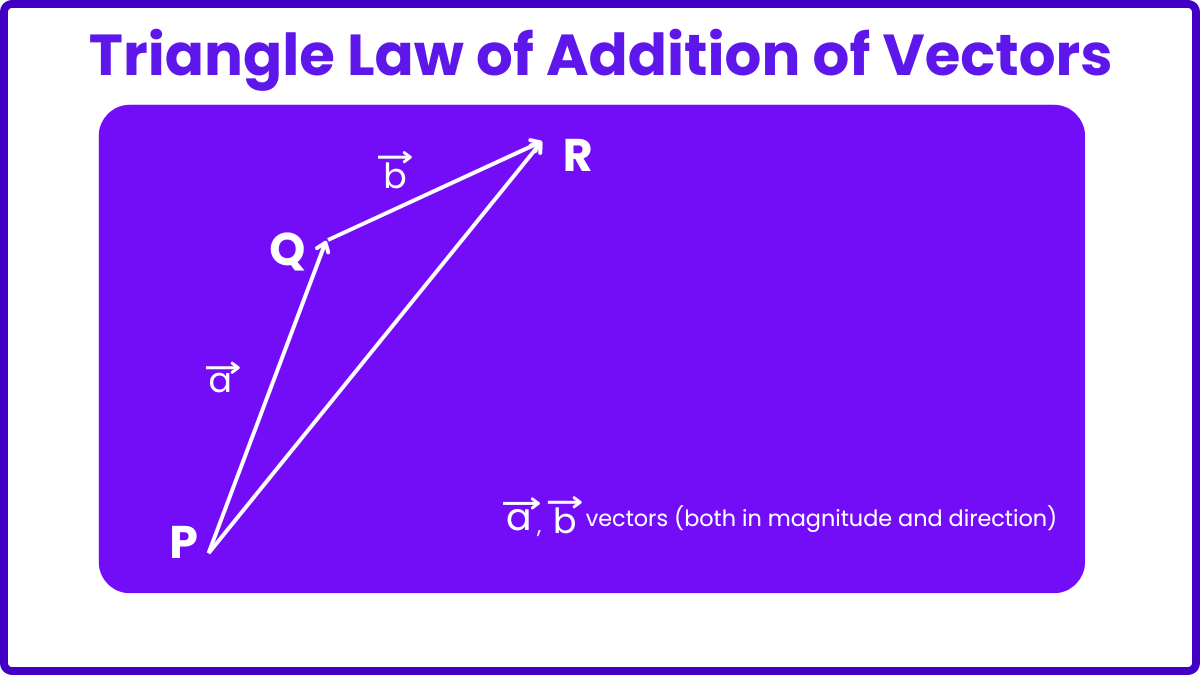
Triangle Law of Addition of Vectors: The law, often referred to as the Triangle Law of Vector Addition, states that if two sides of a triangle represent two vectors in both magnitude and direction, acting simultaneously on a body and arranged sequentially, then the third side of the triangle, when drawn to close the triangle, represents the resultant vector. This principle is crucial for visually determining the combined effect of two vector quantities.

Parallelogram Law of Addition of Vectors: The Parallelogram Law of Vector Addition states that if two vectors, originating from the same point and acting simultaneously, are represented by the adjacent sides of a parallelogram, then the diagonal of the parallelogram, starting from the same point, represents the sum of these two vectors. This diagonal is the resultant vector that effectively combines the magnitude and direction of the original vectors

Vector Subtraction:

Subtracting one vector from another by subtracting their corresponding components.

• Example: If A = (a1, a2) and B = (b1, b2), then A – B = (a1 – b1, a2 – b2).

Scalar Multiplication:

Multiplying a vector by a scalar changes its magnitude but not its direction.

• Example: If A = (a1, a2) and k is a scalar, then kA = (ka1, ka2).

Dot Product (Scalar Product):

A scalar value obtained by multiplying corresponding components of two vectors and summing the results.

• Example: If A = (a1, a2) and B = (b1, b2), then A · B = a1b1 + a2b2.

Cross Product (Vector Product):

A vector perpendicular to two given vectors in three-dimensional space, with a magnitude equal to the area of the parallelogram formed by the two vectors.

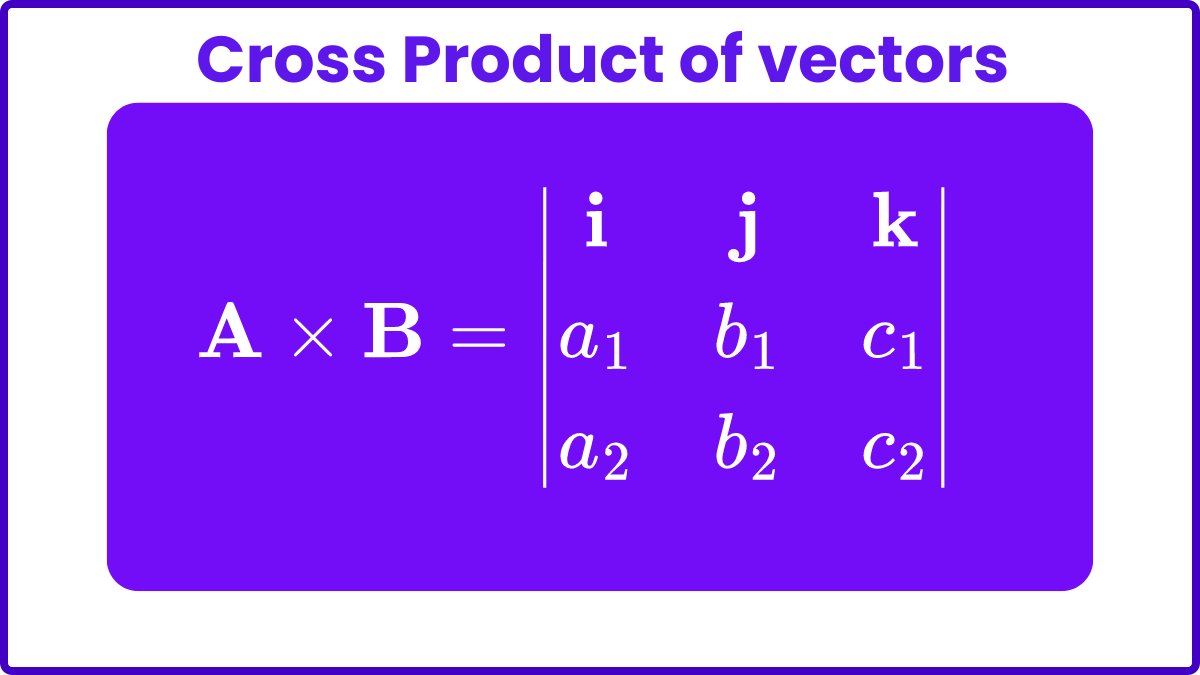
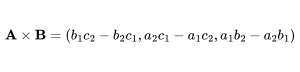
Another way to determine the cross product of two vectors A and B is to determine the product of the magnitudes of the two vectors and the sine of the angle between them.

Magnitude of a Vector:

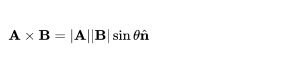
The length or size of the vector, calculated using the Pythagorean theorem.

• Example: If A = (a1, a2), then |A| = √(a1² + a2²).

Unit Vector:

A vector with a magnitude of one, indicating direction. It is obtained by dividing the vector by its magnitude.

• Example: If A = (a1, a2), then the unit vector u = A/|A| = (a1/|A|, a2/|A|).

Vector Algebra Formulas

1) Vector Addition:

Combines corresponding components of vectors A and B.

2) Vector Subtraction:

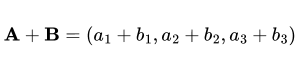
Subtracts corresponding components of vector B from A.

3) Scalar Multiplication:

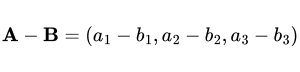
Multiplies each component of vector A by scalar

4) Dot Product (Scalar Product):

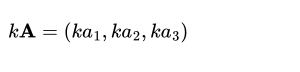
Sum of the products of corresponding components of vectors A and B.

5) Cross Product (Vector Product):

Results in a vector perpendicular to both A and B in three-dimensional space.

6) Magnitude of a Vector:

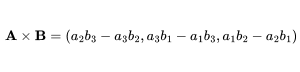
Calculates the length or size of vector A.

7) Unit Vector:

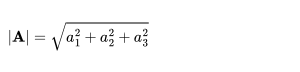
A vector with a magnitude of one, indicating direction.

8) Projection of Vector A on B:

Projects vector A onto vector B.

9) Angle Between Two Vectors:

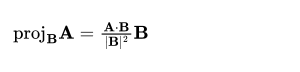
Finds the cosine of the angle θ between vectors A and B.

10) Distance Between Two Points:

Calculates the distance between points (x₁,y₁​,z₁​) and (x₂,y₂,z₂)

Applications of Vector Algebra

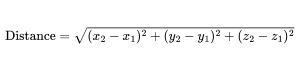
Vector algebra is a pivotal branch of mathematics with wide applications in Physics and Mathematics, particularly because it deals with quantities that have both magnitude and direction, such as velocity, acceleration, and force. These quantities are expressed mathematically as vectors. Here’s an enhanced overview of the applications of vector algebra:

Differential Equations and Geometry: Vector algebra plays a critical role in the study of differential equations and differential geometry. It provides essential tools for describing and solving problems involving multi-dimensional spaces, helping to analyze curves, surfaces, and their properties.

Physics and Engineering Applications: In physics and engineering, vectors are indispensable for modeling and analyzing phenomena associated with electromagnetic fields, gravitational fields, and fluid dynamics. Vectors help in understanding how forces interact in space, offering a clear method for representing field strengths and directions.

Force Analysis: Vector algebra is crucial in breaking down forces into their component parts. This is particularly useful in mechanics and structural engineering, where it is essential to determine the effects of forces acting in various directions.

System Interactions: In physics, vector algebra is used extensively to explore the interactions between multiple vectors. This includes studying the resultant effects when forces, velocities, or other vector quantities combine.

Scalar Triple Product and Coplanarity: The scalar triple product—a calculation involving the dot product of one vector with the cross product of two others—has significant implications in spatial analysis. This product is zero if the vectors are coplanar, meaning they lie in the same plane. This property is used in vector calculus to determine the relationships between vectors in three-dimensional space.

Vector Fields and Flow Lines: Vector algebra also helps in the visualization and analysis of vector fields, which are essential in understanding flow lines in fluid dynamics, as well as field lines in electromagnetic and gravitational fields.

Navigational Techniques: Vectors are used in navigation to plot courses in three-dimensional space, combining direction and magnitude to chart paths effectively, whether in aviation, marine navigation, or space exploration.

Vector Algebra Example

Practice Questions on Vector Algebra

Question 1: Given vectorsa=3i−4j+k and b=−i+2j−2k, find the dot product a⋅b

Question 2: For the vectors from Question 1, compute the cross product a×b.

Question 3: Find a unit vector in the direction of vector c=4i−j+2k

Question 4: Calculate the angle between vectors a\mathbf{a}a and b\mathbf{b}b from Question 1.

Question 5: If d=7i+6j+2k and e=i−2j+2k determine whether vectors d and e are perpendicular.

Answers:

Answer 1: The dot product a⋅b is calculated as:

a⋅b=(3)(−1)+(−4)(2)+(1)(−2)=−3−8−2=−13

Answer 2: The cross product a×b is calculated as:

=i((−4)(−2)−1⋅2)−j(3⋅(−2)−1⋅(−1))+k(3⋅2−(−4)(−1))

=i(8−2)−j(−6+1)+k(6−4)

=6i+5j+2k

Answer 3: The magnitude of C is:

The unit vector in the direction of c is :

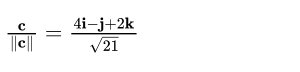
Answer 4: The cosine of the angle θ between a and b is:

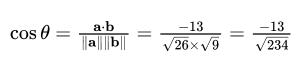
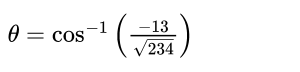
Answer 5: The dot product of d and e is:

d⋅e=(7)(1)+(6)(−2)+(2)(2)=7−12+4=−1

Since d⋅e≠0 , the vectors are not perpendicular.