Which of the following is the correct factorization of the trinomial x² + 5x + 6?
(x+2)(x+3)
(x−2)(x−3)
(x+1)(x+6)
(x−1)(x−6)


Trinomials are a fundamental aspect of algebra that involve expressions made up of three distinct terms. Typically formed by variables, constants, and coefficients linked through operations like addition, subtraction, and multiplication, trinomials are essential for developing complex problem-solving skills in mathematics. Understanding how to manipulate and factor trinomials can unlock a deeper comprehension of equations solving and function analysis. This introduction to trinomials will explore their definitions, various forms, and practical applications in both academic and real-world scenarios. Whether you’re a student or simply refreshing your math skills, mastering trinomials is a step toward advanced algebraic competence.
A trinomial is a type of algebraic expression composed of three distinct terms. It is one of several forms of expressions that collectively fall under the broader category of polynomials. Each term in a trinomial consists of coefficients (constants) and variables, combined using mathematical operations such as addition (+), subtraction (−), multiplication (×), and occasionally division (÷). Alongside trinomials, other types of expressions like monomials (single term), binomials (two terms), and polynomials (many terms) categorize the variety of expressions in algebra. This article will delve into trinomials, explore methods for factoring them, introduce formulas used in the factoring process, and demonstrate these concepts through practical examples.
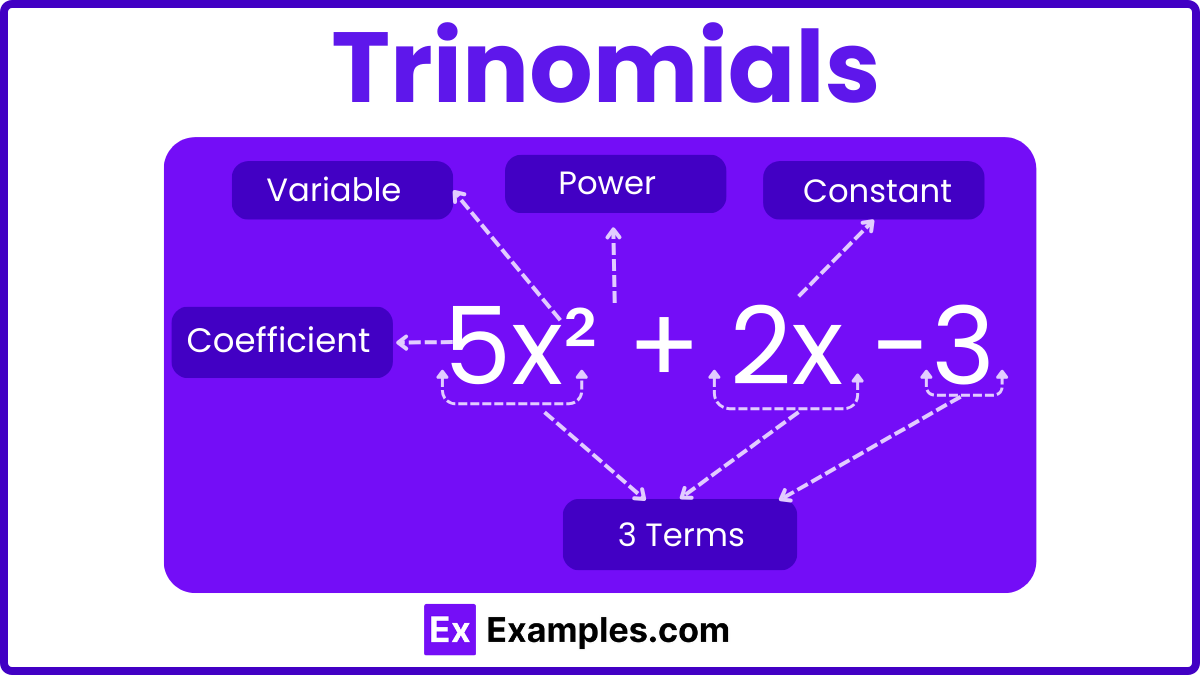
Trinomials, as specific types of polynomial expressions containing exactly three terms, can vary in complexity and structure depending on the powers of the variables and the nature of their coefficients. Understanding the different types of trinomials is crucial for effectively solving, factoring, and applying them in various mathematical contexts. Here are the primary types of trinomials you might encounter:
These are perhaps the most common type of trinomials and have the general form: ax²+bx+c where a, b, and c are constants, and a≠0. The highest power of the variable x is 2. Quadratic trinomials are particularly notable in algebra for their role in various applications, including quadratic equations.
Cubic trinomials are higher-degree polynomials where the highest degree of any term is three. They take the form: ax³+bx²+cx or ax³+bx+ca with constants a, b, and c, and a≠0 . These trinomials appear in more advanced algebra and calculus problems.
A homogeneous trinomial has terms of the same degree. For instance, all terms in the expression: ax³+bx³y+cy³ are of degree three when considering all variables involved. Such trinomials are often used in algebraic geometry and multivariable calculus.
These trinomials include terms of different degrees, such as: ax²+by+c where the variables x and y may have different powers, and the coefficients a, b, and c are constants. Heterogeneous trinomials are common in polynomial equations where variables have different influences.
Linear trinomials involve terms that do not exceed the first degree, typically taking a form similar to: ax+by+cz where a, b, and c are constants, and x, y, and z are variables. These are useful in linear algebra and systems of linear equations.
Factoring a trinomial involves breaking it down into simpler algebraic expressions, typically binomials or monomials, that multiply together to yield the original trinomial. This process is often represented as (x + m)(x + n) for quadratic trinomials, where mmm and nnn are constants that satisfy the equation when expanded. Factoring is a fundamental skill in algebra that simplifies solving equations, finding roots, and analyzing polynomial functions. Various techniques apply depending on the structure and complexity of the trinomial. Let’s explore different methods to factor trinomials, each suited to particular types of trinomial equations.
The general form of quadratic trinomial formula in one variable is ax² + bx + c, where a, b, c are constant terms and neither a, b, or c is zero. For the value of a, b, c, if b² – 4ac > 0, then we can always factorize a quadratic trinomial. It means that ax² + bx + c = a(x + h)(x + k), where h and k are real numbers.
Step 1: Multiply the Coefficient of x²and the Constant Term.
2×3=6
Step 2: Find two numbers that add up to the coefficient of the middle term (7) and multiply to the product obtained in Step 1 (-6).
The numbers are 6 and 1 because 6+1=7 and 6×1=6
Step 3: Rewrite the original equation by replacing the middle term with the two numbers found in Step 2.
2x²+7x+3=2x²+6x+x+3
Step 4: Group the terms in pairs and factor out the common factors from each group.
2x²+6x+x+3=(2x²+6x)+(x+3)
Factoring out the common factors in each group:
=2x(x+3)+1(x+3)
Step 5: Factor out the common binomial.
The common binomial from both terms is (x+3):
=(x+3)(2x+1)
Therefore, (x+3) and (2x+1) are the factors of 2x²+7x+3
There is no specific way to solve a quadratic trinomial in two variables. Let’s take an example.
Example: x² + 6xy + 7y²

A trinomial can be a perfect square or a non-perfect square. We have two formulas to factorize a perfect square trinomial. But for factorizing a non-perfect square trinomial, we do not have any specific formula, instead, we have a process.
To factorize a trinomial of the form ax2 + bx + c, we can use any of the below-mentioned formulas:
A trinomial identity typically refers to an equation that expresses a relationship between trinomials in a way that holds true for all permissible values of the variables involved. Trinomial identities can be quite useful in simplifying complex algebraic expressions and solving equations more efficiently. Here are some commonly used trinomial identities in algebra:
One of the most well-known trinomial identities is the square of a sum:
(a+b)²=a²+2ab+b²
This identity indicates that squaring a binomial (a sum of two terms) results in a trinomial.
Similarly, the square of a difference is:
(a−b)²=a²−2ab+b²
This identity also produces a trinomial and is particularly useful in algebraic manipulations involving squares of expressions.
While not a trinomial itself, it leads to a product of binomials:
a²−b²=(a−b)(a+b)
This identity is crucial in factorization and solving quadratic equations.
These are specific forms of trinomials that arise from the square of binomials:
Both expand into a trinomial, perfectly illustrating how certain binomial squares inherently produce trinomial identities.
Although more complex, the expansion of the cube of a sum or difference also results in identities involving trinomials:
(a+b)³=a³+3a²b+3ab²+b³
(a−b)³=a³−3a²b+3ab²−b³
While these result in four terms, their manipulations often involve simplifying to or from trinomials in certain cases.
Trinomial: x²+5x+6
Answer: x²+5x+6=(x+2)(x+3)
Trinomial: 3x²−12x+12
Answer: 3x²−12x+12=3(x²−4x+4)=3(x−2)²
Trinomial: 2x²−7x−15
Answer: 2x²−7x−15=(2x+3)(x−5)
Trinomial: x²−4x+4
Answer: x²−4x+4=(x−2)²
Trinomial: 6x²+11x−35
Answer: 6x²+11x−35=(2x−5)(3x+7)
Trinomial: 4x²+4x−24
Answer: 4x²+4x−24=4(x²+x−6)=4(x+3)(x−2)
Trinomial: x²+x−20
Answer: x²+x−20=(x+5)(x−4)
Trinomial: 5x²−14x+8
Answer: 5x²−14x+8=(5x−4)(x−2)
A trinomial is an algebraic expression composed of three terms, typically involving variables, coefficients, and constants, connected by addition or subtraction operations.
A polynomial is a mathematical expression consisting of variables, coefficients, and exponents arranged in terms through addition, subtraction, multiplication, and non-negative integer exponents. A trinomial is a specific type of polynomial with exactly three terms.
To factor trinomials quickly, identify products and sums that fit the trinomial’s coefficients, apply the AC method for splitting the middle term, and use grouping to factorize the expression into binomials.
A simple trinomial is an algebraic expression of the form ax²+bx+c, where a, b and c are the constants, and x is a variable, with straightforward coefficients often conducive to easy factoring.
A trinomial is an algebraic expression made up of three terms, which can be numbers, variables, or both, combined with mathematical operations such as addition or subtraction.
Three examples of trinomials are x²+5x+6, 3x²−12x+12, and 2x²−7x−15.
To solve a trinomial, especially when set equal to zero, factor it into binomials, set each binomial equal to zero, and solve for the variable. This method is commonly used to find the roots of quadratic equations.
No, a trinomial cannot have four terms. By definition, a trinomial always consists of exactly three terms. An expression with four terms is called a quadrinomial.
A perfect trinomial is a squared binomial, resulting in a form like ax²+2abx+b² or a² – 2abx + b², where the middle term and the constants relate perfectly to square the binomial.
After trinomial, terms referring to expressions with more terms include quadrinomial (four terms), and more generally, polynomial, which refers to any expression with one or more terms.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
Which of the following is the correct factorization of the trinomial x² + 5x + 6?
(x+2)(x+3)
(x−2)(x−3)
(x+1)(x+6)
(x−1)(x−6)
Which of the following is a trinomial?
\( x^2 + 3x + 2 \)
\( x + 1 \)
\( x^3 + 2x^2 \)
\( 5x^2 \)
What is the sum of the trinomials \( 2x^2 + 3x + 4 \) and \( x^2 - x + 1 \)?
\( 3x^2 + 2x + 5 \)
\( 3x^2 + 4x + 5 \)
\( 3x^2 + 2x + 3 \)
\( 3x^2 + 2x + 4 \)
What is the product of the trinomials \( (x + 1)(x^2 - x + 2) \)?
\( x^3 + x^2 - x + 2 \)
\( x^3 + 2x^2 + x + 2 \)
\( x^3 + x^2 + x + 2 \)
\( x^3 + 3x^2 + 2x + 2 \)
Which trinomial can be factored as \( (x + 2)(x + 3) \)?
\( x^2 + 5x + 6 \)
\( x^2 + 4x + 3 \)
\( x^2 + 6x + 9 \)
\( x^2 + 3x + 2 \)
Which of the following is the standard form of a trinomial?
\( 3x^2 + x + 4 \)
\( 4 + x + 3x^2 \)
\( x + 4 + 3x^2 \)
\( x^2 + 4x + 2 \)
What is the factored form of the trinomial \( x^2 + 7x + 12 \)?
\( (x + 1)(x + 12) \)
\( (x - 3)(x + 4) \)
\( (x + 3)(x + 4) \)
\( (x + 6)(x + 2) \)
Which trinomial represents a perfect square?
\( x^2 + 6x + 9 \)
\( x^2 + 5x + 6 \)
\( x^2 + 7x + 10 \)
\( x^2 + 8x + 15 \)
What is the discriminant of the trinomial \( x^2 + 4x + 4 \)?
0
4
8
16
Which trinomial cannot be factored over the integers?
\( x^2 + 2x + 5 \)
\( x^2 + 3x + 2 \)
\( x^2 + 5x + 6 \)
\( x^2 + 4x + 4 \)
Before you leave, take our quick quiz to enhance your learning!

