Which of the following is true for a matrix that is both symmetric and skew-symmetric?
It must be a diagonal matrix.
It must be the zero matrix.
It must be an identity matrix.
It can be any matrix.
of 10
Matrices – Definition, Types, Formulas, Examples
Matrices – Definition, Types, Formulas, Examples
What are Matrices?
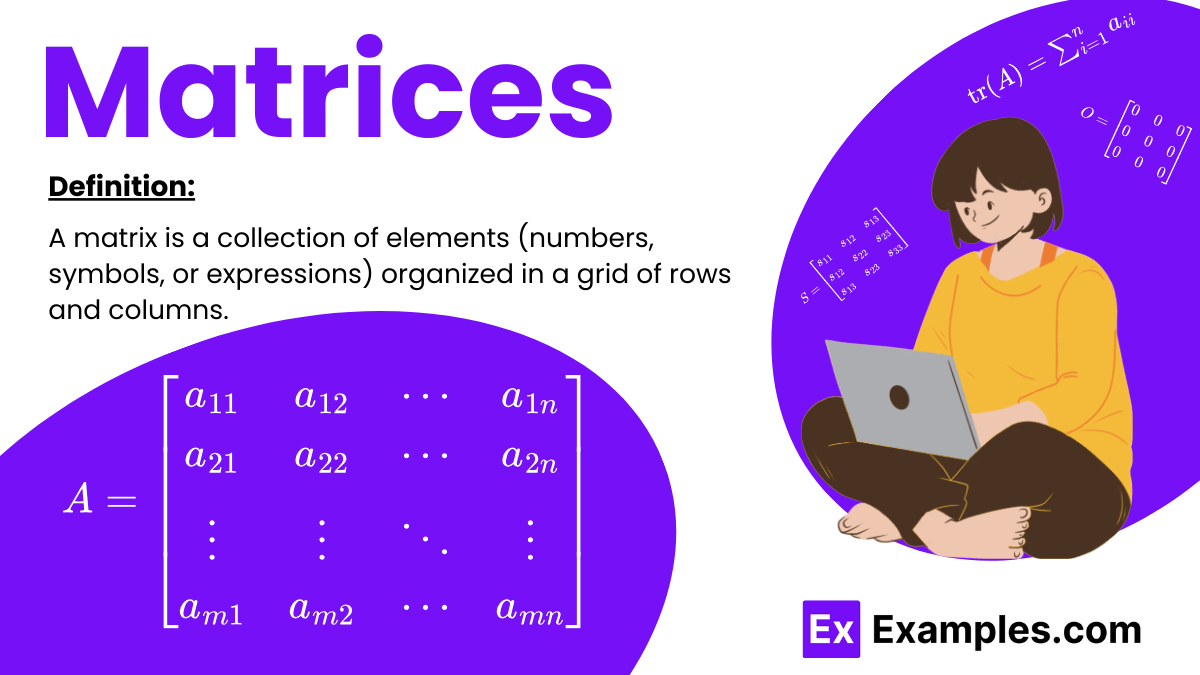
A matrix is a collection of elements (numbers, symbols, or expressions) organized in a grid of rows and columns. Each element in a matrix is identified by its position in the grid, typically denoted as aija_{ij}, where ii is the row number and jj is the column number.
Types of Matrices
1. Row Matrix
A row matrix has only one row.
2. Column Matrix
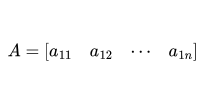
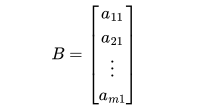
A column matrix has only one column.
3. Square Matrix
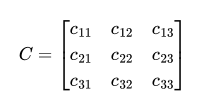
A square matrix has the same number of rows and columns.
4. Diagonal Matrix
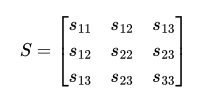
A diagonal matrix is a square matrix where all elements outside the main diagonal are zero.
5. Identity Matrix
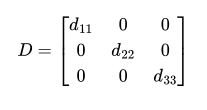
An identity matrix is a diagonal matrix where all diagonal elements are 1. It is denoted by I.
6. Zero Matrix (Null Matrix)
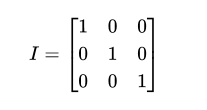
A zero matrix has all its elements equal to zero.
7. Symmetric Matrix
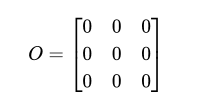
A symmetric matrix is a square matrix that is equal to its transpose (A=AT).
8. Skew-Symmetric Matrix
A skew-symmetric matrix is a square matrix where the transpose is equal to its negative (AT=−A).
9. Upper Triangular Matrix
An upper triangular matrix is a square matrix where all elements below the main diagonal are zero.
10. Lower Triangular Matrix
A lower triangular matrix is a square matrix where all elements above the main diagonal are zero.
11. Orthogonal Matrix
An orthogonal matrix is a square matrix whose rows and columns are orthogonal unit vectors (orthonormal vectors). The transpose of an orthogonal matrix is also its inverse (AT=A−1A^T = A^{-1}AT=A−1).
12. Singular Matrix
A singular matrix is a square matrix that does not have an inverse. Its determinant is zero.
13. Non-Singular Matrix
A non-singular matrix is a square matrix that has an inverse. Its determinant is non-zero.
Matrix Operations
Matrix operations are fundamental in linear algebra and are used extensively in various fields such as physics, engineering, computer science, and economics. Here are the key matrix operations:
1. Matrix Addition
To add two matrices A and B, they must have the same dimensions. The sum is obtained by adding corresponding elements.
2. Matrix Subtraction
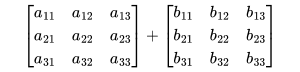
Similar to addition, to subtract matrix B from matrix A, they must have the same dimensions. The difference is obtained by subtracting corresponding elements.
,
3. Scalar Multiplication
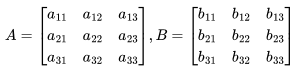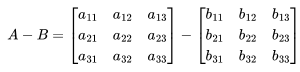
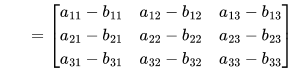
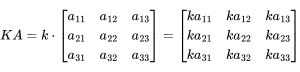
Multiplying a matrix A by a scalar k involves multiplying each element of A by k.
4. Matrix Multiplication
The product of two matrices A and B is defined if the number of columns in A equals the number of rows in B. The element cijc_{ij}cij in the resulting matrix C is the dot product of the i-th row of A and the j-th column of BBB.
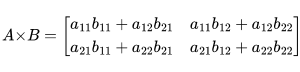
Properties of Matrix Multiplication
There are different properties associated with the multiplication of matrices. For any three matrices A, B, and C:
- AB ≠ BA
- A(BC) = (AB)C
- A(B + C) = AB + AC
- (A + B)C = AC + BC
- A = A = AIₙ, for identity matrices I𝑚 and Iₙ.
- Aₘ ₓ ₙOₙ ₓ ₚ=Oₘ ₓ ₚ, where O is a null matrix.
5. Matrix Transposition
The transpose of a matrix A is obtained by swapping its rows with its columns. The transpose of A is denoted by Aᵀ
6. Matrix Inversion
The inverse of a square matrix A is denoted by A⁻¹ and is defined as the matrix that, when multiplied by A, results in the identity matrix. Not all matrices have an inverse; a matrix must be non-singular (its determinant is non-zero) to have an inverse.
AA⁻¹=A⁻¹A=I
7. Determinant
The determinant is a scalar value that is a function of a square matrix. It is denoted as det (A) or ∣A∣ and provides important properties, such as whether a matrix is invertible. For a 2×2 matrix:
8. Trace
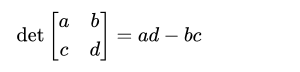
The trace of a square matrix A is the sum of its diagonal elements. It is denoted by tr(A)
Matrices Formulas
- A(adj A) = (adj A) A = | A | Iₙ
- | adj A | = | A |ⁿ⁻¹
- adj (adj A) = | A |ⁿ⁻² A
- | adj (adj A) | = | A |⁽ⁿ⁻¹⁾²
- adj (AB) = (adj B) (adj A)
- adj (Aᵐ) = (adj A)ᵐ,
- adj (kA) = kⁿ⁻¹ (adj A) , k ∈ R
- adj(In) = In
- adj 0 = 0
- A is symmetric ⇒ (adj A) is also symmetric.
- A is diagonal ⇒ (adj A) is also diagonal.
- A is triangular ⇒ adj A is also triangular.
- A is Singular⇒| adj A | = 0
- A⁻¹ = (1/|A|) adj A
- (AB)⁻¹ = B⁻¹A⁻¹
Notation of Matrices
Matrix notation is a systematic way of organizing data or numbers into a rectangular array using rows and columns. Each entry in the matrix is typically represented by a variable with two subscripts indicating its position within the matrix.
Here is examples to illustrate matrix notation:
Example 1: 2×3 Matrix
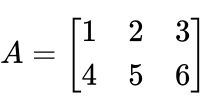
Consider a matrix A of size 2×3 (2 rows and 3 columns)
- (Row 1, Column 1)
- (Row 1, Column 2)
- (Row 1, Column 3)
- (Row 2, Column 1)
- (Row 2, Column 2)
- (Row 2, Column 3)
Important Notes on Matrices:
- Cofactor of the matrix A is obtained when the minor Mᵢⱼ of the matrix is multiplied with (-1)ᶦ⁺ʲ
- Matrices are rectangular-shaped arrays.
- The inverse of matrices is calculated by using the given formula: A-1 = (1/|A|)(adj A).
- The inverse of a matrix exists if and only if |A| ≠ 0.
What is the Difference Between Matrix and Matrices?
A “matrix” is a singular term describing a rectangular array of numbers. “Matrices” is the plural form, referring to multiple such arrays.
What Are Matrices Used For?
Matrices are used to solve systems of linear equations, perform geometric transformations, and handle data in fields like economics, engineering, and computer science.
What is the Definition of Matrices?
Matrices are rectangular arrays of numbers, symbols, or expressions arranged in rows and columns, used in various mathematical computations.
What Are the 4 Types of Matrices?
The four types of matrices include square, diagonal, scalar, and identity matrices, each having unique properties and applications.
How Matrix is Used in Real Life?
In real life, matrices are used for graphics transformations, cryptography, economic modeling, and network analysis, simplifying complex calculations.
What Are the 7 Types of Matrix?
The seven types of matrices are square, rectangular, diagonal, scalar, identity, zero, and triangular matrices, each serving specific mathematical purposes.
Is Matrices Algebra or Calculus?
Matrices belong to the field of algebra, specifically linear algebra, which deals with vectors, vector spaces, and linear transformations.
Is Matrix Calculus or Algebra?
Matrix operations are primarily algebraic. Matrix calculus refers to applying calculus operations like differentiation to matrices.
Why Are Matrices Important in Real Life?
Matrices are crucial in real life for modeling physical systems, performing data analysis, and optimizing processes across various disciplines.
How to Understand Matrices?
To understand matrices, start with basic operations like addition and multiplication, then explore their applications in solving linear equations and transformations.
Share :
Practice Test
What is the determinant of a 2x2 matrix \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\)?
\( ac - bd \)
\( ab + cd \)
\( ad - bc \)
\( ad + bc \)
of 10
What is the condition for a matrix to be invertible?
The determinant of the matrix must be zero.
The matrix must be a square matrix.
The matrix must be symmetric.
The matrix must have non-zero elements.
of 10
If matrix \( A \) is a 3x3 identity matrix, what is \( A^2 \)?
\( 2A \)
Zero matrix
\( A \)
\( A^3 \)
of 10
For a matrix \( A \) and its inverse \( A^{-1} \), which of the following is true?
\( A \cdot A^{-1} = I \)
\( A \cdot A^{-1} = A \)
\( A^{-1} \cdot A = 0 \)
\( A^{-1} \cdot A = I \)
of 10
What does the term "null space" of a matrix refer to?
The set of all vectors that are mapped to the zero vector by the matrix.
The set of all vectors that span the matrix.
The set of all eigenvalues of the matrix.
The set of all rows of the matrix.
of 10
How do you compute the inverse of a 2x2 matrix \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\)?
\(\frac{1}{a + d} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)
\(\frac{1}{a - d} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)
\(\frac{1}{ad + bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)
\(\frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)
of 10
If a matrix is diagonal, what is its determinant?
The product of its diagonal elements.
The sum of its diagonal elements.
Zero.
The product of its off-diagonal elements.
of 10
How is the matrix transpose of a matrix \( A \) defined?
Swapping the elements along the diagonal.
Swapping the rows and columns of \( A \).
Adding the matrix to itself.
Subtracting the matrix from itself.
of 10
Which of the following matrices is the zero matrix?
\(\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}\)
\(\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)
\(\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\)
\(\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}\)
of 10