What is the square of 105?
11025
11105
11105
11500
of 10
Square & Square Root of 1764 – Examples, Methods, Calculation
Square & Square Root of 1764 – Examples, Methods, Calculation
In the domain of mathematics, particularly in algebraic studies, the core principles of squares and square roots are paramount. Squaring a number, demonstrated by multiplying 105 by itself to yield 11025, is foundational. It unveils properties inherent in rational numbers (expressible as a fraction) and irrational numbers (not neatly fractionable). A grasp of these fundamentals enriches understanding of mathematical relationships and patterns, serving as a cornerstone for further exploration. Through the study of squares and square roots, insights into numerical behavior emerge, aiding in the analysis of complex mathematical structures.
Square of 105
105² (105 × 105) = 11025
In algebraic mathematics, understanding square numbers is crucial. The square of 105 is calculated by multiplying 105 by itself, resulting in 11025. This operation is fundamental for exploring mathematical properties and patterns, providing insights into the behavior of numbers within mathematical contexts.
Square Root of 105
√105 = 10.246950766
Or
√105 = 10.246 Upto 3 decimals
In algebraic mathematics, the square root of 105 is essential. Calculated as an irrational number approximately equal to 10.24695077, it is the number whose square equals 105. Understanding square roots enriches comprehension of mathematical relationships, offering insights into numerical behavior and patterns.
Square Root of 105: 10.246950766
Exponential Form: 105^½ or 105^0.5
Radical Form: √105
Is the Square Root of 105 Rational or Irrational?
The square root of 105 is an irrational number
The square root of 105 is irrational because it cannot be expressed as a fraction of two integers. Therefore, it is not a rational number.
Rational Number:
A rational number can be expressed as a fraction of two integers, denoted as a/b, where the denominator isn’t zero. Examples encompass positive, negative, or zero values, like 3/4, -5/2, 0, 1, -2, etc.
Example: For instance, consider 3/4; since both 3 and 4 are integers, and the denominator isn’t zero, 3/4 is rational.
Irrational Number:
An irrational number, such as √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, thus it defies representation in the form a/b.
Example: Take √2; it has a non-repeating, non-terminating decimal expansion (√2 ≈ 1.41421356…), rendering it irrational.
Method to Find Value of Root 105
To find the value of the square root of 105, you can use various methods such as:
Prime Factorization: Break down 105 into its prime factors.
Long Division: Utilize long division to iteratively approximate the square root.
Estimation: Estimate the square root based on nearby perfect squares.
Square Root of 105 by Long Division Method
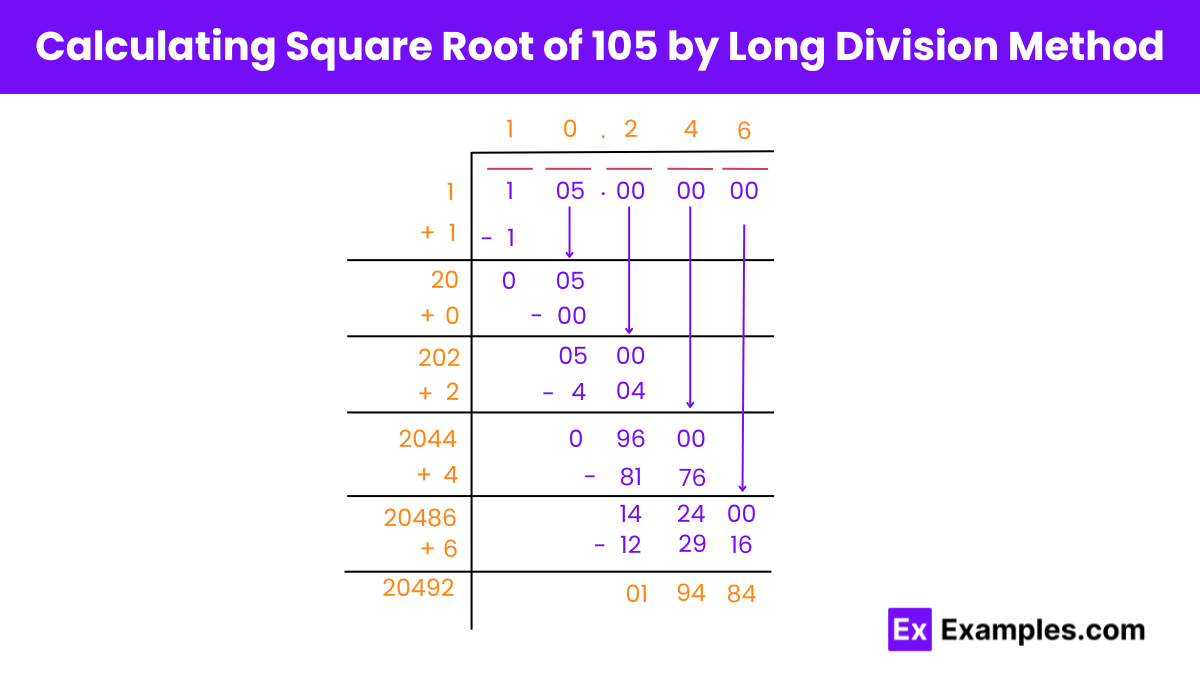
Step 1: Pairing Digits
Begin by grouping digits in pairs from the right side of the number 105. In this case, there are two pairs: 05 and 1.
Step 2: Initial Division
Find a number (n) whose square is less than or equal to 1. Here, n = 1 since 1 × 1 = 1 ≤ 1. The quotient is thus 1.
Step 3: New Divisor
Add the divisor (n) with itself to obtain the new divisor (2n), which equals 2.
Step 4: Bringing Down the Next Pair
Bring down the next pair (005) to form the new dividend.
Step 5: Finding the Next Digit
Find a digit (A) such that 2A × A is less than or equal to 5. Here, A = 0.
Step 6: Decimal Placement and Iteration
Place a decimal point after 5 in the dividend and after 1 in the quotient. Add three pairs of zeros to the dividend after the decimal and repeat the previous steps for these pairs.
Step 7: Conclusion
Continue this process until the desired level of precision is achieved. In this case, the square root of 105 is approximately 10.246 by the long division method.
105 is Perfect Square root or Not?
No, 105 is not a perfect square number
105 is not a perfect square because its square root is an irrational number. It cannot be expressed as the exact integer value without decimal approximation, indicating that it is not a perfect square.
FAQS
What are the properties of the square root of 105?
The square root of 105 is an irrational number that cannot be expressed as a fraction of two integers
Are there any practical applications of knowing the square and square root of 105?
Knowledge of the square and square root of 105 may be useful in various mathematical and scientific calculations.
How does understanding the square and square root of 105 enrich mathematical comprehension?
Understanding the properties and relationships of the square and square root of 105 deepens comprehension of mathematical concepts and patterns.
Where can I find more information about squares, square roots, and their relevance to 105?
Additional information about squares, square roots, and their relevance to 105 can be found in mathematics textbooks, online resources, and educational websites.
Share :
Practice Test
Find the square root of 11025.
103
104
105
106
of 10
Which of the following is the approximate value of the square root of 105?
10.24
10.25
10.26
10.27
of 10
What is the square of 105.5?
11050.25
11100.25
11153.25
11200.25
of 10
Find the square root of 11130.25.
105.5
106.5
107.5
108.5
of 10
Which of the following is closest to the square of 104.9?
10980.01
11001.61
11024.01
11041.21
of 10
What is the square root of 11024.01?
104.7
104.8
104.9
104.0
of 10
What is the square of 105.1?
11050.51
11062.01
11065.01
11068.51
of 10
What is the square root of 11065.01?
105.0
105.1
105.2
105.3
of 10
Find the square root of 11073.04.
105.1
105.2
105.3
105.4
of 10