Square & Square Root of 108
Square & Square Root of 108
Within algebraic studies, understanding squares and square roots is pivotal. Squaring, exemplified by multiplying a number like 108 by itself to yield 11664, is foundational. This operation is key in exploring rational and irrational numbers. Comprehending these concepts enriches mathematical understanding, revealing patterns and relationships. Squares and square roots are fundamental in unraveling mathematical intricacies, essential for discerning the properties of rational and irrational numbers. Mastery of these concepts not only strengthens algebraic proficiency but also fosters a deeper appreciation of mathematical intricacies and the interplay between numbers and their properties.
Square of 108
A square number, such as the square of 108, is obtained by multiplying 108 by itself, resulting in 11664. Square numbers, inherent in algebra, illustrate foundational concepts and serve as building blocks for understanding mathematical relationships. They demonstrate the fundamental operation of squaring within mathematical exploration.
Square Root of 108
Or
√108 = 10.392 Upto 3 decimals
The square root of 108, a fundamental concept in mathematics, is approximately 10.39. It represents the number that, when multiplied by itself, yields 108. Understanding square roots elucidates algebraic principles and aids in solving equations. They are essential in deciphering the roots of numbers and their mathematical significance.
Square Root of 108: 10.3923048454
Exponential Form: 108^½ or 108^0.5
Radical Form: √108
Is the Square Root of 108 Rational or Irrational?
The square root of 108 is irrational. This means it cannot be expressed as a fraction of two integers. It is a non-repeating, non-terminating decimal, indicating its irrational nature.
Rational Numbers:
Rational numbers are expressed as the quotient or fraction of two integers, where the denominator is not zero. They take the form a/b, where both a and b are integers, and b is not zero.
Examples : 1/2, 3/4, and 5/7. Any integer can also be represented as a rational number by placing it over 1.
Irrational Numbers:
Irrational numbers cannot be expressed as fractions and possess non-repeating, non-terminating decimal representations. They do not conform to the quotient of two integers.
Examples : π, √2, and e. These numbers exhibit infinite and non-repeating decimal expansions.
Methods to Find Value of Root 108
There are several methods to find the value of the square root of 108:
Prime Factorization Method: Break down 108 into its prime factors (2² × 3²). Then, extract the square root of each prime factor and multiply them together.
Estimation Method: Use approximation techniques such as the Babylonian method or successive approximation to approximate the square root of 108.
Calculator: Utilize a scientific calculator or an online calculator to directly compute the square root of 108.
Table Lookup: Refer to mathematical tables or tables of square roots to find the approximate value of the square root of 108.
Square Root of 108 by Long Division Method
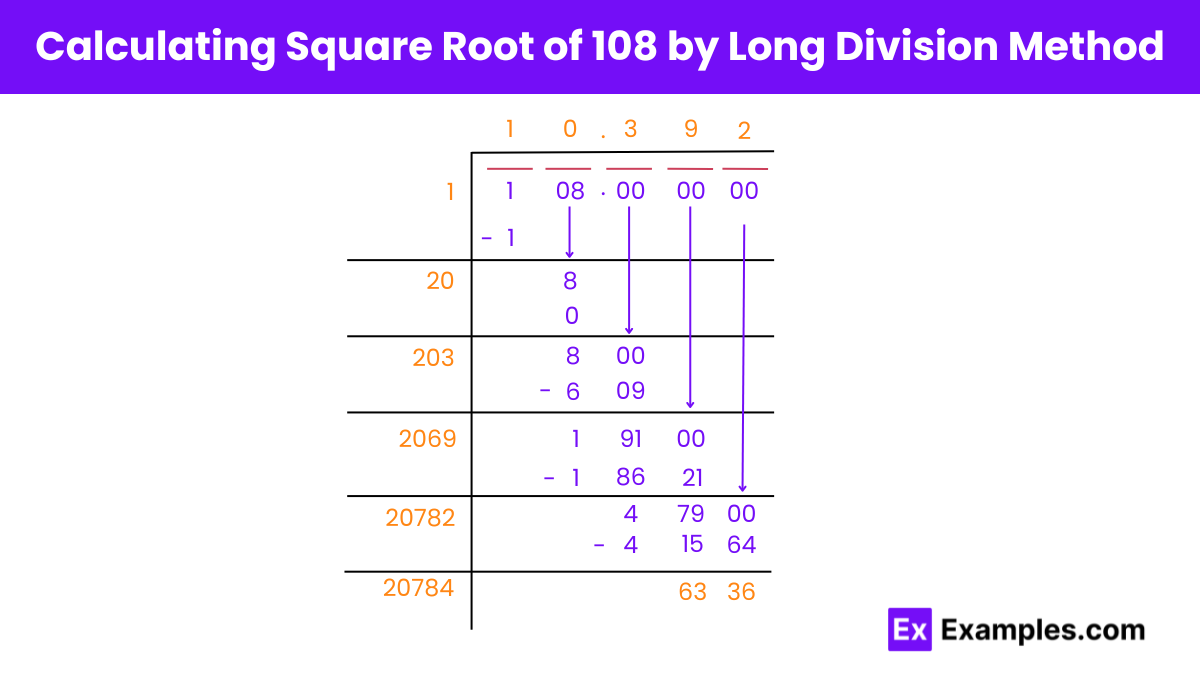
Finding the Square Root of 108 by Long Division Method
Prepare the Number: Write 108.000000 and group digits in pairs from the right: 08 (pair) and 1 (standalone).
Initial Division: Divide 1 by a number, finding a quotient of 1 and a remainder of 0.
Double the Quotient: Double 1 to get 2, setting up 20 as the new divisor.
Next Pair of Digits: Bring down 08 for division, giving 800 as the new dividend.
Trial and Error: Find a number to add to 200 (the doubled quotient) so that the product is 800 or less. In this case, it’s 3, resulting in 203 as the new divisor.
Update Quotient and Remainder: 3 becomes part of the quotient, and the remainder becomes 191.
Iterate: Continue the process until reaching desired precision (3 decimal places).
Final Result: The square root of 108 is approximately 10.392.
Is 108 Perfect Square root or Not
No, 108 is not a perfect square, as it does not have an integer square root. The square root of 108 is approximately 10.3923, which is not a whole number. Therefore, 108 is not a perfect square.
FAQ’S
How Does Knowing the Square Root of 108 Help in Mathematics?
Understanding the square root of 108 helps in various mathematical calculations, problem-solving, and understanding the concept of irrational numbers.
Can 108 be Written as the Sum of Two Squares?
Yes, 108 can be written as the sum of two squares: 108 = 9² + 3².
What is the Importance of Squares and Square Roots in Mathematics?
Squares and square roots are fundamental concepts in mathematics, used in various fields such as algebra, geometry, and calculus. They help in solving equations, understanding patterns, and analyzing data.
Are There Applications of the Square Root of 108 in Real Life?
Yes, the square root of 108 and similar mathematical concepts are used in various real-life applications such as engineering, physics, finance, and computer science.
Can I Simplify the Square Root of 108 Further?
No, the square root of 108 cannot be simplified further because it is an irrational number. It can only be approximated to a certain number of decimal places.
Share :
