What is the square of 117?
13689
13989
14400
13600
of 10
Square & Square Root of 117
Square & Square Root of 117
Square of 117
The square number of 117 is 13,689. A square number is obtained by multiplying a number by itself. In this case, 117 multiplied by 117 equals 13,689. Square numbers hold significance in algebraic studies, showcasing fundamental operations and laying the groundwork for exploring mathematical relationships and patterns.
Square root of 117
√117= 10.816653826391969
or
√117= 10.816 upto 3 decimals
The square root of 117, an irrational number, is approximately 10.816653826391969. It represents the number that, when multiplied by itself, equals 117. Understanding square roots illuminates mathematical principles, offering insights into numerical relationships and facilitating problem-solving across various disciplines.
Is the Square Root of 117 Rational or Irrational?
A number is considered irrational if it cannot be expressed as a simple fraction (i.e., as the ratio of two integers). The square root of 117 cannot be expressed this way, and its decimal representation is non-repeating and non-terminating: approximately 10.816653826391969. Therefore,√117 is an irrational number.
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. Rational numbers include fractions, integers, and terminating or repeating decimals.
Methods to Find Value of Root 117
Prime Factorization Method:
Decompose 117 into its prime factors: (117 = 3× 3×13).
Pair the prime factors in groups of two: (3 ×3 = 9) (one pair).
Since 13 is left alone, it remains outside the square root.
Thus, √117= = 3√13.
Estimation Method:
Find perfect squares close to 117: (11² = 121) and (10² = 100).
Since 117 is closer to 121 than 100, you can estimate the square root of 117 to be between 10 and 11.
A closer estimation can be found using averages: (10=+11)/2= 10.5.
Use 10.5 as a starting point for iterative methods like Newton’s method or the Babylonian method.
Iterative Methods:
Newton’s Method: Use the formula (xₙ₊₁ = 1/2 (xₙ + 117/xₙ) with an initial guess. Repeat until convergence.
Babylonian Method: Use the formula (xₙ₊₁ = 1/2 (xₙ + 117/xₙ)) iteratively until the value converges to the square root of 117.
Using a Calculator or Computer:
Most calculators and computers have built-in functions to calculate square roots directly. Simply input 117 and find the square root.
Square Root of 117 by Long Division Method
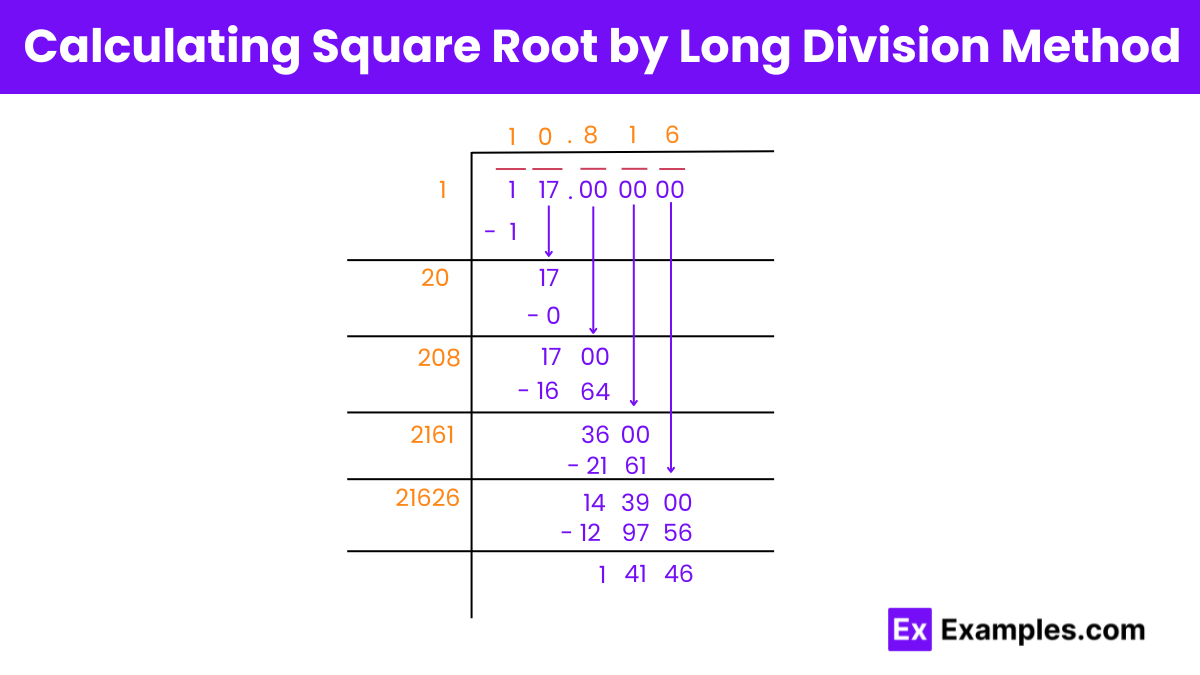
Step 1: Begin by pairing the digits of 117 from right to left. Place a horizontal bar to indicate the pairs. Since 117 has two digits, we have one pair, 17, and a single digit 1.
Step 2: Find a number that, when multiplied by itself, gives a product less than or equal to 1. We know (1 × 1 = 1).
Step 3: Multiply the quotient (initially 0) by 2. This gives us 2, which becomes the starting digit of the new divisor.
Step 4: Place 0 at the units place of the new divisor, resulting in 20. Multiply 20 by 0 to get 0. The answer is now 1, and we bring down 00.
Step 5: Multiply the quotient (now 10) by 2. This gives 20, the starting digits of the new divisor.
Step 6: Place 8 at the units place of the new divisor (208) because (208 × 8 = 1664). The remainder obtained is 36, and we bring down 00.
Step 7: Multiply the quotient (now 108) by 2. This gives 216, the starting digits of the new divisor.
Step 8: Place 1 at the units place of the divisor (2161) because (2161×1 = 2161). The answer obtained is 1439. Next, bring down the next pair of numbers, 00.
Step 9: Multiply the quotient (now 1081) by 2. This gives 2162, the starting digits of the new divisor.
Step 10: Place 6 at the units place of the divisor (21626) because (21626× 6 = 129756). The remainder obtained is 14144. Continue these steps until achieving the desired number.
Is 117 Perfect Square root or Not
A perfect square is a number that can be expressed as the product of an integer multiplied by itself. Since there is no integer ( n ) such that ( n×n = 117 ), 117 is not a perfect square.
FAQs
What is the cube root of 117?
The cube root of 117 is approximately ( 4.973 ) when rounded to three decimal places.
What is 117 divisible by?
The cube root of 117 is approximately ( 4.973 ) when rounded to three decimal places.
How to simplify the square root of 117?
117 is divisible by 1, 3, 9, 13, 39, and 117.
Share :
Practice Test
What is the square root of 13,689?
115
117
120
123
of 10
What is the approximate value of the square root of 117?
10.8
10.9
11.0
11.1
of 10
Which number is closest to the square of 117?
13600
13700
13689
13800
of 10
If x² = 117, what is the approximate value of ?
10.8
10.9
11.0
11.1
of 10
Which statement is true about the square root of 117?
It is a whole number.
It is a rational number.
It is an irrational number.
It is an integer.
of 10
What is the result of 117 squared minus 50?
13639
13689
13739
13789
of 10
Which of the following is the closest integer to the square root of 117?
10
11
12
13
of 10
What is the difference between 14000 and the square of 117?
3000
3010
3020
3030
of 10
If the square root of a number is approximately 10.9, what is the number?
117
118
119
220
of 10