Square & Square Root of 1225 – Methods , Calculations , Examples

In the realm of mathematics, particularly in algebra, understanding how to manipulate numbers through squaring and finding square roots is crucial. This guide zeroes in on the number 1225, demonstrating its squaring process which yields 1,500,625, and detailing the computation of its square root, which is exactly 35. These operations are excellent examples of algebra at work, illustrating the application of algebraic principles to solve real-world problems and understand complex mathematical patterns.

Square of 1225

The square of 1225 refers to the result obtained when the number 1225 is multiplied by itself. Mathematically, this operation is expressed as 1225². When calculated, the square of 1225 is 1,500,625. This squaring process is a fundamental arithmetic operation that helps in various mathematical contexts, such as computing areas, understanding quadratic relationships, and analyzing patterns within numerical data.

Square Root of 1225

The square root of 1225 refers to the number that, when multiplied by itself, results in 1225. In mathematical terms, this is expressed as √1225​. For the number 1225, the square root is 35, as 35×35=1225. Understanding square roots is crucial for solving various mathematical problems, including quadratic equations, geometric measurements, and in many real-life applications where determining underlying values from square results is necessary.

Is the Square Root of 1225 Rational or Irrational?

Rational:

The square root of 1225 is rational. A rational number is defined as a number that can be expressed as the fraction 𝑝𝑞​, where 𝑝 and 𝑞 are integers, and 𝑞 is not zero. The square root of 1225 is 35, which can be expressed as 35/1​. It fits perfectly into the category of rational numbers because it results in an integer without any need for an infinite or non-repeating decimal.

Irrational:

In contrast, a number is considered irrational if it cannot be expressed as a simple fraction where both the numerator and the denominator are integers, with the denominator not being zero. Irrational numbers have non-repeating, non-terminating decimal expansions. However, since the square root of 1225 is 35, a whole number, it is not irrational.

Methods to Find the Value of Root 1225

Finding the square root of 1225 can be done using several methods, each offering a clear pathway to understanding and determining the value. Here are a few commonly used methods:

1. Prime Factorization

• Begin by factorizing 1225 into its prime factors. Since 1225=5²×7², the square root can be found by taking the root of each prime factor:
• √1225=√5²×7²=5×7=35.

2. Using a Calculator

• The simplest and quickest method; just type 1225 into a calculator and press the square root function to get the exact value of 35.

3. Estimation

• If you do not have access to a calculator, you can estimate the square root by finding numbers you know the squares of that are near 1225. For example, you know 30²=900 and 40²=1600. Since 1225 is closer to 900, you start estimating around 30 and find that 35²=1225.

4. Using Exponent Rules

• Recognize that 1225 can be expressed as 35². This straightforward observation leads directly to the square root:
• √1225=√352²=35.

Square Root of 1225 by Long Division Method

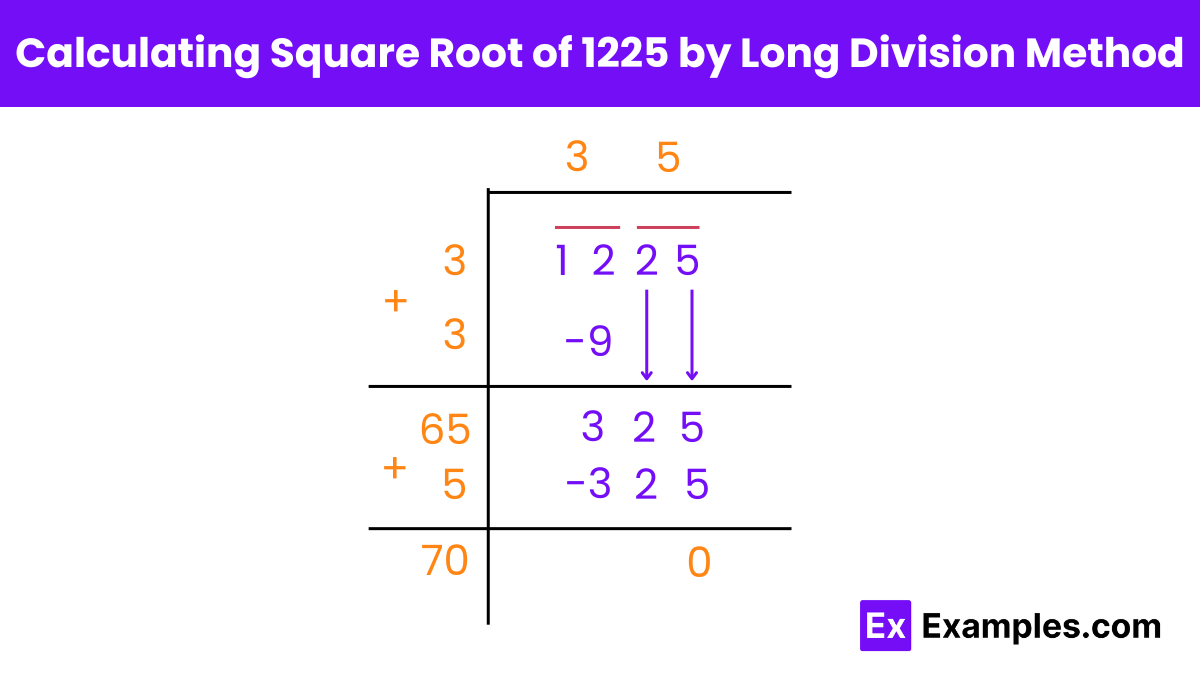
To find the square root of 1225 using the long division method, you’ll follow a step-by-step process that breaks down the number systematically. Here’s how to do it:

1. Set up the number: Arrange the digits of 1225 in pairs from right to left. For 1225, this will be 12 | 25.
2. Find the largest square less than or equal to the first pair (12): The largest perfect square less than 12 is 9 (3²), so write 3 as the first digit of the quotient above the pair.
3. Subtract the square from the first pair and bring down the next pair: Subtract 9 from 12 to get a remainder of 3. Bring down the next pair, making it 325.
4. Double the quotient: Double the current quotient (which is 3), making it 6. This number will be the beginning of your next divisor.
5. Find the next digit of the quotient: Look for a digit 𝑋 to place next to 6 in the quotient (making it 6X) and as the last digit in the divisor (60X + X), such that (60𝑋+𝑋)×𝑋≤325. 𝑋 will be 5 because 65×5=325.
6. Complete the calculation: Subtract 325 from 325 to get a remainder of 0. Your quotient, which is now 35, is the square root of 1225.

1225 is Perfect Square root or Not?

Yes, 1225 is a perfect square. A number is considered a perfect square if it can be expressed as the square of an integer. In the case of 1225, it is the square of 35, since 35×35=1225. Thus, it meets the criteria to be classified as a perfect square, with its square root being a whole number.

FAQS

What can be multiplied to get 1225?

To get 1225, you can multiply the number 35 by itself, as 35×35=1225. Another combination includes multiplying 49 by 25, since 49×25=1225, demonstrating the different factor pairs that result in 1225.

What is the least common multiple of 1225?

The least common multiple (LCM) of 1225 and any of its factors is 1225 itself, since it is the smallest number that all factors of 1225 can divide without leaving a remainder.

What prime numbers make 1225?

The prime numbers that make up 1225 are 5 and 7, expressed in its prime factorization as 5²×7². These prime numbers are squared to form the composite number 1225.

How does the knowledge of square roots like that of 1225 assist in real-world measurements?

Understanding square roots like that of 1225 is essential in fields like surveying and construction, where precise area calculations are necessary.

Is the square root of 1225 used in solving quadratic equations?

Yes, knowing that the square root of 1225 is 35 can be used to solve quadratic equations where 1225 is a term.