What is the approximate square root of 123?
10
11
12
13


In the domain of mathematics, particularly in algebraic studies, the foundational principles of squares and square roots are of utmost significance. Squaring a number, as demonstrated by multiplying a number by itself, such as 123 squared yielding 15129, is a fundamental operation. It forms a cornerstone in exploring the properties of both rational numbers (expressible as a fraction of two integers) and irrational numbers (which cannot be expressed as a neat fraction). Understanding these basic concepts enhances one’s grasp of mathematical relationships and patterns.
123² (123 × 123) = 15129
A square number results from multiplying a number by itself, like the square of 123, yielding 15129. In mathematics, understanding squares and their roots is fundamental. They illuminate properties of rational and irrational numbers, enriching comprehension of mathematical relationships and patterns.
√123 = 11.0905365064
Or
√123 = 11.090 Upto 3 decimals
The square root of a number, such as the square root of 15129, which is 123, uncovers the original value. This fundamental concept in mathematics, exemplified by the square of 123, elucidates properties of both rational and irrational numbers, deepening understanding of mathematical principles and patterns.
Square Root of 123: 11.0905365064
Exponential Form: 123^½ or 123^0.5
Radical Form: √123
The square root of 123 is an irrational number
The square root of 123 is irrational because it cannot be expressed as a fraction of two integers. It is a non-repeating, non-terminating decimal, demonstrating its irrational nature.
Rational Number:
A rational number is expressible as the quotient or fraction of two integers, with a non-zero denominator. It’s written as a/b, where a and b are integers. Examples include 3/4, -5/2, 0, 1, -2, etc.
Example: Take 3/4; it’s expressed as a fraction, with 3 as the numerator and 4 as the denominator. As both are integers and the denominator isn’t zero, 3/4 is rational.
Irrational Number:
An irrational number is a real number not expressible as a ratio of two integers. Its decimal representation neither terminates nor repeats, and it can’t be written as a/b, where a and b are integers and b isn’t zero. Examples include √2, π, and φ.
Example: For √2, its decimal expansion is approximately 1.41421356…, non-repeating and infinite. Unable to be written as a fraction of two integers, √2 is irrational.
To find the value of √123, you can use various methods:
Approximation: Use estimation methods like Newton’s method or approximation techniques to get a close value.
Prime Factorization: Decompose 123 into its prime factors to simplify the root.
Decimal Expansion: Use algorithms like long division or Newton’s method to compute the decimal approximation of √123.
Calculator: Utilize a calculator with a square root function for an accurate numerical value.
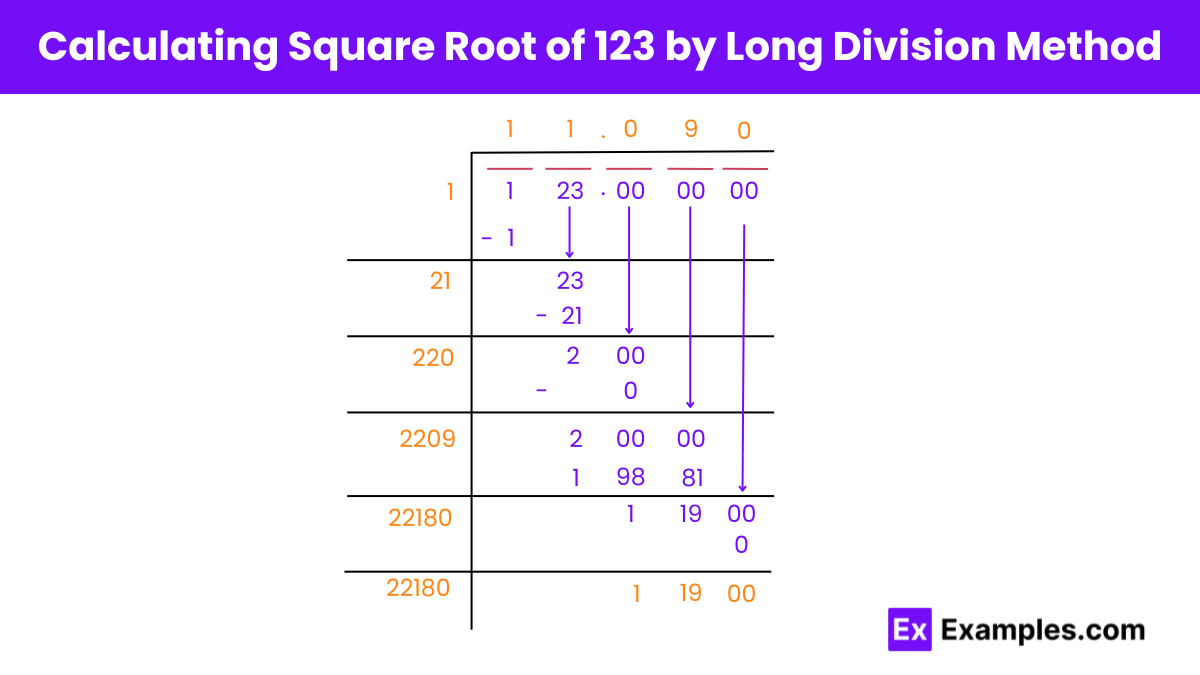
Finding the Square Root of 123 by Long Division Method
Step 1: Preparation
Write 123 as 1 23.00 00 00 and group the digits in pairs. The digit ‘1’ is left alone.
Step 2: Initial Division
Divide the first digit ‘1’ by finding a number × number such that the result is ≤ 1. We get 1 × 1 = 1. The remainder is 0.
Step 3: Bringing Down the Next Pair
Bring down the next pair ’23’ for division. Double the quotient obtained, resulting in 2. The new divisor becomes 20.
Step 4: Iterative Division
Find a number such that (number + 20) × number results ≤ 23. We find (1 + 20) × 1 = 21. Subtract this from 23 to get a remainder of 2.
Step 5: Continuing the Process
Bring down the next pair ’00’. Double the quotient obtained, yielding 22. The new divisor becomes 220.
Step 6: Further Iteration
Find a number such that (number + 220) × number results ≤ 200. We find (0 + 220) × 0. The remainder remains 200.
Step 7: Repeating the Process
Continue the process until reaching the desired level of precision, approximating the square root of 123 to 3 decimal places.
No, 123 is not a perfect square number
123 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since 123 cannot be expressed as the product of an integer multiplied by itself, it is not a perfect square.
123 is a natural number that appears in various mathematical contexts but does not hold any particular significance on its own.
No, the square root of 123 cannot be simplified further because 123 does not have any perfect square factors.
No, 123 is not a prime number because it has divisors other than 1 and itself.
Applications include calculating distances, areas, volumes, and in engineering and physics where precise measurements are required.
The factors of 123 are 1, 3, 41, and 123. However, none of these factors are perfect squares, indicating that 123 is not a perfect square.
The square root of -123 is a complex number, denoted as ±√(-123), which lies in the realm of complex numbers.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the approximate square root of 123?
10
11
12
13
What is the square of 12?
144
122
130
156
Which of the following is the closest whole number to the square root of 123?
10
11
13
12
What is the result of squaring 11?
121
123
130
144
Which number squared is closest to 123?
11
12
13
14
What is the square of the number that is closest to the square root of 123?
121
144
169
100
What is the approximate value of the square root of 123 to the nearest whole number?
10
11
12
13
What is 11.1 squared?
123.21
122.21
130.21
140.21
What is the difference between 144 and 123?
10
15
21
25
Which value is closer to the square root of 123: 11.1 or 11.2?
11.1
11.2
Both are equally close
Neither is close
Before you leave, take our quick quiz to enhance your learning!

