What is the square of 145?
21025
20850
20725
21100
of 10
Square & Square Root of 145 – Methods, Calculation, How to find
Square & Square Root of 145 – Methods, Calculation, How to find
In the realm of , mathematics particularly in algebra, squares and square roots are fundamental concepts. They are essential for understanding the nature of rational and irrational numbers. When we square a number like 145, we delve into these foundational operations, enriching our grasp of mathematical relationships and patterns.
Square of 145
A square number, such as 145, is the result of multiplying an integer by itself. The square of 145 is 21,025, illustrating key algebraic principles and deepening our understanding of mathematical relationships and patterns within algebra and beyond.
Square Root of 145
or
√145 ≈ 12.041 upto to three decimal places
The square root of 145, which is not a perfect square, is approximately 12. Mastering square roots involves identifying the number that, when multiplied by itself, equals 145. This is crucial for exploring algebraic relationships and patterns within mathematics.
Exponential Form: 145^1/2 or 145^0.5
Radical Form: √145
Is the Square Root of 145 Rational or Irrational?
Rational Numbers : Rational numbers can be expressed as fractions of two integers.
Irrational Numbers : Irrational numbers cannot be expressed as fractions of integers.
Since the square root of 145 is not a perfect square, it is irrational. It cannot be expressed as a fraction of two integers.
Methods to Find the Value of √145
- Estimation Method: Start with an initial guess and refine it iteratively using methods like Newton-Raphson.
- Prime Factorization Method: Express 145 as a product of prime factors, then find the square root of each prime factor.
- Calculator: Use a calculator with a square root function to compute√145 directly.
Square Root of 145 by Long Division Method
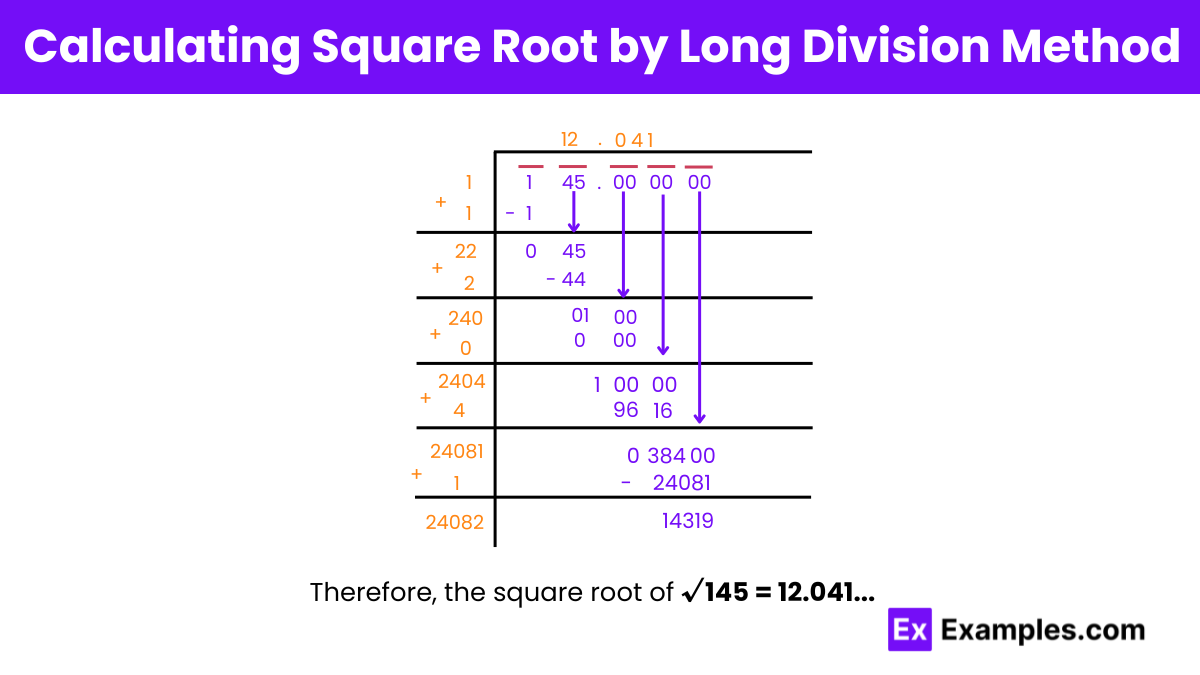
Step 1: Identify the first digit: Find a number ( a ) whose square is less than or equal to 1. The value of ( a ) will be 1, as ( 1× 1 = 1≤ 1 ).
- Quotient: 1
- New divisor: ( 2a = 2 )
Step 2 : Form the new dividend: Drag the next pair down (45), making the new dividend 45. Find a number ( A ) such that ( 2A× A ≤ 45 ). In this case, ( A ) will be 2, as ( 2 × 2 × 2 = 8 ≤ 45 ).
Step 3 : Update quotient: Now, the quotient becomes 12. Place a decimal point after 2 in the quotient and in the original number, turning it into 145.00.
Step 4 : Extend the process: Add three pairs of zeros to the dividend after the decimal (145.000000). Repeat the process for each pair of zeros:
- New divisor: ( 12 × 2 = 24 )
- Drag down the next pair (00), making the new dividend 0000.
- Find the largest ( A ) such that ( 240 A× A ≤ 0000 ). Repeat this step for accuracy.
Is 145 a Perfect Square?
A perfect square is a number that can be expressed as the product of an integer with itself. In other words, there must be an integer ( n ) such that ( n × n = 145 ). For 145, there is no such integer, as its square root √145 is approximately 12.0415946, which is not an integer. Therefore, 145 cannot be expressed as the square of any integer, confirming that it is not a perfect square.
Is the square of 145 used in real-world applications?
Yes, squares and square roots are used in various fields, including engineering, physics, and finance for calculations and modeling.
Can prime factorization help find the square root of 145?
Yes, but 145 does not have easily paired prime factors for simple square root calculation.
What is the geometric interpretation of squaring 145?
Squaring 145 represents the area of a square with each side measuring 145 units.
Is 145 a prime number?
No, 145 is not a prime number; it factors into 5 × 29.
Share :
Practice Test
What is the square root of 21025?
143
144
145
146
of 10
Which of the following numbers is closest to the square root of 145?
12
12.05
12.1
12.2
of 10
What is the approximate square root of 145 to the nearest whole number?
11
12
13
14
of 10
The square of which of the following is closest to 145?
12
13
14
15
of 10
What is the value of √145 in decimal form rounded to two decimal places?
12.04
12.10
12.20
12.30
of 10
If x² =145, what is the value of ?
12
12.04
12.1
12.2
of 10
Which number squared is just above 145?
12
13
14
15
of 10
What is the square of 13?
169
144
156
175
of 10
The value of √145 falls between which two consecutive integers?
11 and 12
12 and 13
13 and 14
14 and 15
of 10