Square & Square Root of 147
Square & Square Root of 147
In the domain of mathematics, particularly within algebra, squares and square roots hold paramount importance. They serve as the cornerstone upon which our comprehension of rational and irrational numbers is built. By considering a number like 147 and squaring it, we unveil the fundamental essence of this operation, facilitating a deeper exploration of mathematical relationships and patterns.
Square of 147
A square number, such as 147, arises from multiplying an integer by itself. The square of 147 equals 21,609, showcasing algebraic principles and enriching our understanding of mathematical relationships and patterns within algebraic studies and beyond.
Square Root of 147
or
√147 ≈ 12.124 upto 3 decimals
The square root of 147, a perfect square number, is approximately 12.124. Mastering square roots involves identifying the number that, when multiplied by itself, equals 147. This understanding is crucial for exploring algebraic relationships and patterns within mathematics.
Exponential Form: 147^1/2 or 147^0.5
Radical Form: √147
Is the Square Root of 147 Rational or Irrational?
Rational Numbers : Rational numbers are expressible as fractions of two integers.
Irrational Numbers : Irrational numbers cannot be expressed as fractions of integers.
Since the square root of 147 is not a perfect square, it is irrational. It cannot be expressed as a fraction of two integers.
Methods to Find the Value of Root 147
- Estimation Method: Begin with an initial approximation and refine it iteratively using methods like Newton-Raphson.
- Prime Factorization Method: Express 147 as a product of prime factors, then find the square root of each prime factor.
- Calculator: Utilize a calculator with a square root function to directly compute the square root of 147.
Square Root of 147 by Long Division Method
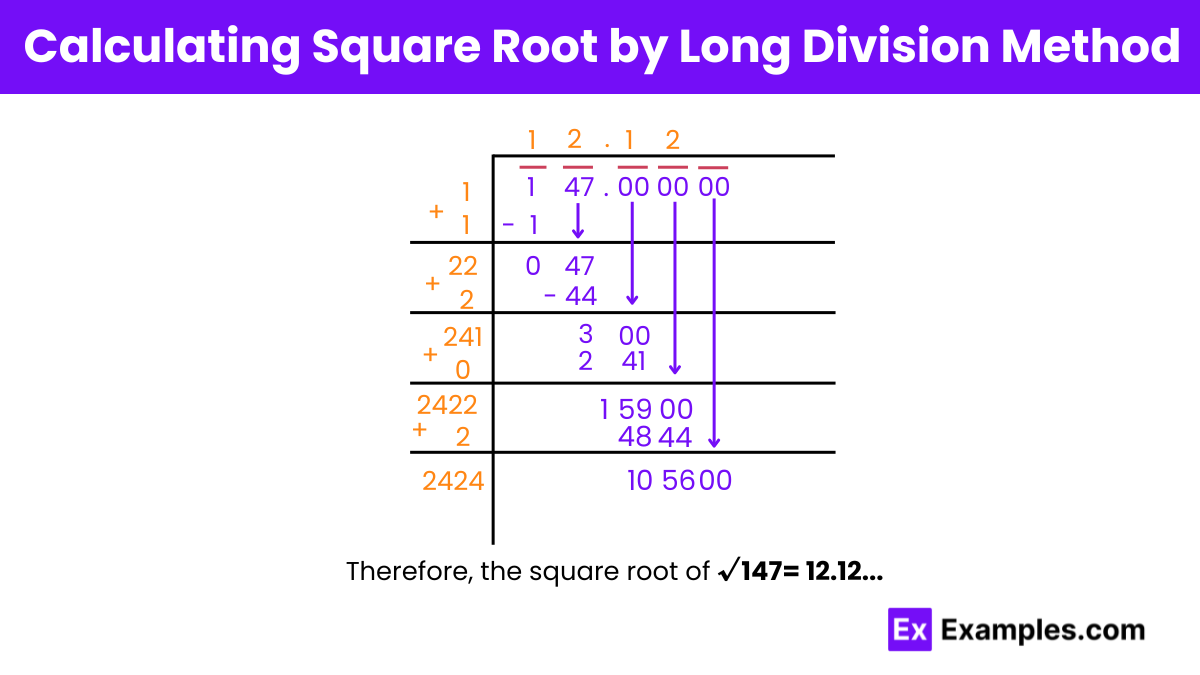
Step 1: Pairing Digits
Starting from the right, we’ll pair up the digits 147 by placing a bar above 47 and 1 separately. Additionally, we’ll pair the 0s in the decimal part in pairs of 2 from left to right.
Step 2: Finding Initial Quotient
Find a number that, when multiplied by itself, results in a product less than or equal to 1. Since this is 1, place 1 in the quotient and divisor’s place, resulting in a remainder of 0.
Step 3: Bringing Down
Drag down 47 beside the remainder 0. Also, add the divisor to itself and write it below (1 + 1 = 2).
Step 4: Continuing Division
Find a number ( X ) such that ( 2X × X ) results in a number less than or equal to 47. The number 2 fits here, so fill it next to 2 in the divisor as well as next to 1 in the quotient.
Step 5: Expanding the Divisor
Find the remainder and now drag down the pair of 0s from the decimal part of the number. By adding ( X ) to the divisor, the new divisor becomes 24.
Step 6: Repeat
Repeat this process iteratively to obtain additional decimal places as needed.
147 is a Perfect Square or Not
147 is not a perfect square because it cannot be expressed as the product of an integer multiplied by itself. In other words, there are no integers where the product of the integer with itself equals 147.
What is the product of 2 and 4 radical 147?
The product of (2) and (4 √147) is (8 √147).
What are the factors of 147?
The factors of 147 are 1, 3, 7, 21, 49, and 147.
What is the prime factorization of root 147?
The prime factorization of (√147) is (3 √147)
What is 147 divisible by?
147 is divisible by 1, 3, 7, 21, 49, and 147.
Share :
