What is the square of 162?
26244
32400
2916
28000
of 10
Square & Square Root of 162 – Methods, Calculation, How to find
Square & Square Root of 162 – Methods, Calculation, How to find
In mathematics, especially in algebra, squares and square roots are fundamental concepts. Squaring a number like 162 involves multiplying it by itself to get 26244. This operation is crucial for exploring properties of rational and irrational numbers, enhancing comprehension of mathematical relationships and patterns. Squares reveal numerical interactions, forming the basis of algebraic analysis, while square roots unveil the origins of numbers, highlighting their significance in mathematical frameworks. Mastering these concepts enhances mathematical prowess and analytical skills.
Square of 162
A square number, like 162, is obtained by multiplying a number by itself. The square of 162 equals 26244. Understanding square numbers elucidates their role in algebraic analysis, showcasing their significance in mathematical patterns and relationships, which is essential for comprehending fundamental mathematical concepts and their applications.
Square Root of 162
Or
√162 = 12.716 Upto 3 decimals
The square root of 162, when squared, equals 162. It’s the number that, when multiplied by itself, gives 162. The square root, approximately 12.727, unveils the origin of 162. Understanding square roots elucidates their role in algebraic analysis, showcasing their significance in mathematical patterns and relationships.
Exponential Form: 162^1/2 or 162^0.5
Radical Form: √162
Is the Square Root of 162 Rational or Irrational?
A rational number is one that can be expressed as the ratio of two integers.
An irrational number cannot be expressed as such a ratio and has a non-repeating, non-terminating decimal expansion.
Methods to Find Value of Root 162
Method 1: Estimation and Trial-and-Error
- Estimate:
Since ( 162 ) is between ( 144 ) and ( 169 ), which are the squares of ( 12 ) and ( 13 ) respectively, we know that √162 is between (12) and ( 13 ). - Trial-and-Error:
Test values between ( 12 ) and ( 13 ) to refine the estimate.
12.5² = 156.25 (too low)
12.6² = 158.76 (too low)
12.7² = 161.29 (very close)
12.8² = 163.84 (too high) - Conclusion:
√162 is approximately ( 12.7 ).
Method 2: Long Division
- Set up long division:
Start with ( 162.000000 ). - Find the square root digit by digit:
Follow the long division process to find the square root of ( 162 ) to the desired precision.
Method 3: Newton’s Method (Iterative)
- Initial Guess: Start with an initial guess ( x₀ ) close to the actual value of √162, for example, ( x₀ = 12 ).
- Iterative Calculation: Use the iterative formula ( xₙ₊₁} = 1/2( xₙ + 162/xₙ) to successively improve the approximation.
- Repeat: Continue iterating until the desired level of precision is reached.
Square Root of 162 by Long Division Method
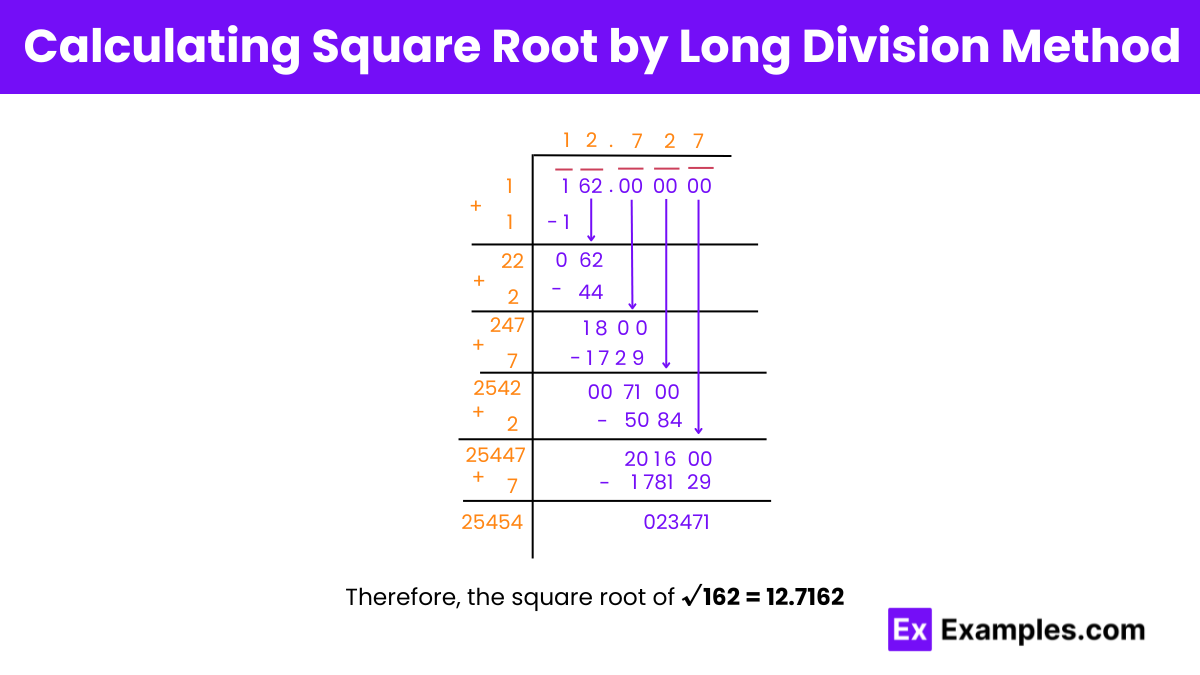
Step 1: Find a number (n) which when multiplied with itself (n × n ≤ 1). So, (n) will be (1) since (1 ×1 = 1).
Step 2: Now, we get the quotient as (1). Also, we have to add the divisor (n) with itself to get the new divisor. The new divisor here will be (2).
Step3: Bring down the pair (62). So, our new dividend is (62). Now find a number (m) such that (2m× m≤ 62). The number (m) will be (2) as (2²×2 = 4× 2 = 8 ≤ 62).
Step 4: Add a decimal in the dividend and quotient part simultaneously. Also, add 3 pairs of zero in the dividend part.
162 is Perfect Square root or Not
A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In other words, perfect squares are the squares of integers. For example, ( 9 ) is a perfect square because ( 3 × 3 = 9 ).
FAQs
What are the square factors of 162?
The square factors of 162 are (1), (9), and (81), as (1² = 1), (3² = 9), and (9² = 81).
What is 162 cubed square root?
The cube root of 162 is approximately 5.4508
What is the 4th square root of 162?
The fourth root of 162 is approximately 3.0723.
What is rationalizing factor of √162?
The rationalizing factor of √162 is ( 3√2} ), achieved by multiplying both the numerator and denominator by (√2).
Share :
Practice Test
What is the square root of 2916?
150
162
170
180
of 10
Which of the following numbers is closest to the square root of 162?
12.7
12.8
13
13.2
of 10
What is the approximate square root of 162 to the nearest whole number?
12
13
14
15
of 10
The square of which of the following is closest to 162?
12
13
14
15
of 10
What is the value of √162 in decimal form rounded to two decimal places?
12.72
12.82
12.90
12.75
of 10
If x² = 162, what is the value of ?
12.7
12.72
13
12.8
of 10
Which number squared is just above 162?
12
13
14
15
of 10
What is the square of 14?
196
182
210
202
of 10
The value of √162 falls between which two consecutive integers?
12 and 13
13 and 14
11 and 12
14 and 15
of 10