What is the approximate value of the square root of 178?
13.33
13.41
13.25
13.50
of 10
Square & Square Root of 178 – Examples, Methods, Calculation
Square & Square Root of 178 – Examples, Methods, Calculation
In tthe realm of mathematics, particularly within algebraic studies, the foundational concepts of squares and square roots are of paramount importance. Squaring a number, exemplified by taking a number like 178 and multiplying it by itself to yield a result of 31684, is a fundamental operation. This operation serves as a cornerstone in investigating the properties inherent in both rational numbers (those expressible as a fraction of two integers) and irrational numbers (which defy expression as a neat fraction). A comprehension of these fundamental concepts enriches one’s understanding of mathematical relationships and patterns, essential for exploring the intricate interplay between algebraic expressions and numerical values.
Square of 178
178²(178 × 178) = 31684
The square of 178, a square number, is 31684. In mathematics, squaring involves multiplying a number by itself, revealing its inherent properties. Understanding square numbers is fundamental, shedding light on mathematical relationships and paving the way for exploring algebraic concepts and numerical patterns with precision and depth.
Square Root of 178
√178 = 13.34166
Or
√178 = 13.341 Upto 3 decimals
The square root of 178, denoted as √178, is approximately 13.3417. In mathematics, finding the square root involves determining a number that, when multiplied by itself, equals the original number. Understanding square roots illuminates numerical relationships, aiding in solving equations and grasping the essence of mathematical structures.
Square Root of 178 : 13.3417
Exponential Form : 178^½ or 178^0.5
Radical Form : √178
Is the Square Root of 178 Rational or Irrational?
The square root of 178 is irrational.
The square root of 178 is irrational. This means it cannot be expressed as a fraction of two integers. Instead, it is a non-repeating, non-terminating decimal, indicating its irrational nature.
Certainly! Here’s a revised version:
Rational Number:
A rational number is a fraction of two integers, expressed as a/b, where a and b are integers and b ≠ 0. Examples include 3/4, -5/2, 0, 1, -2, etc.
Example: 3/4 is rational because it’s a fraction with both numerator and denominator as integers, and the denominator isn’t zero.
Irrational Number:
An irrational number cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating. Examples include √2, π, and φ.
Example: The square root of 2, √2, has a decimal expansion of approximately 1.41421356…, which is non-repeating and infinite, making it irrational.
Methods to Find the Value of Root 178
There are several methods to find the value of the square root of 178:
Prime Factorization: Express 178 as a product of its prime factors, then identify pairs of identical factors. Take one factor from each pair and multiply them to find the square root.
Estimation: Use estimation techniques to approximate the square root of 178, possibly by considering known square roots nearby, such as 169 (13^2) and 196 (14^2).
Newton’s Method: Iteratively refine an initial guess until it converges to the square root of 178 using Newton’s method for root finding.
Calculator: Utilize a scientific calculator or online calculator to directly compute the square root of 178. Most calculators have a square root function that provides accurate results.
Choose the method that best suits your preference and level of mathematical proficiency.
Square Root of 178 by Long Division Method
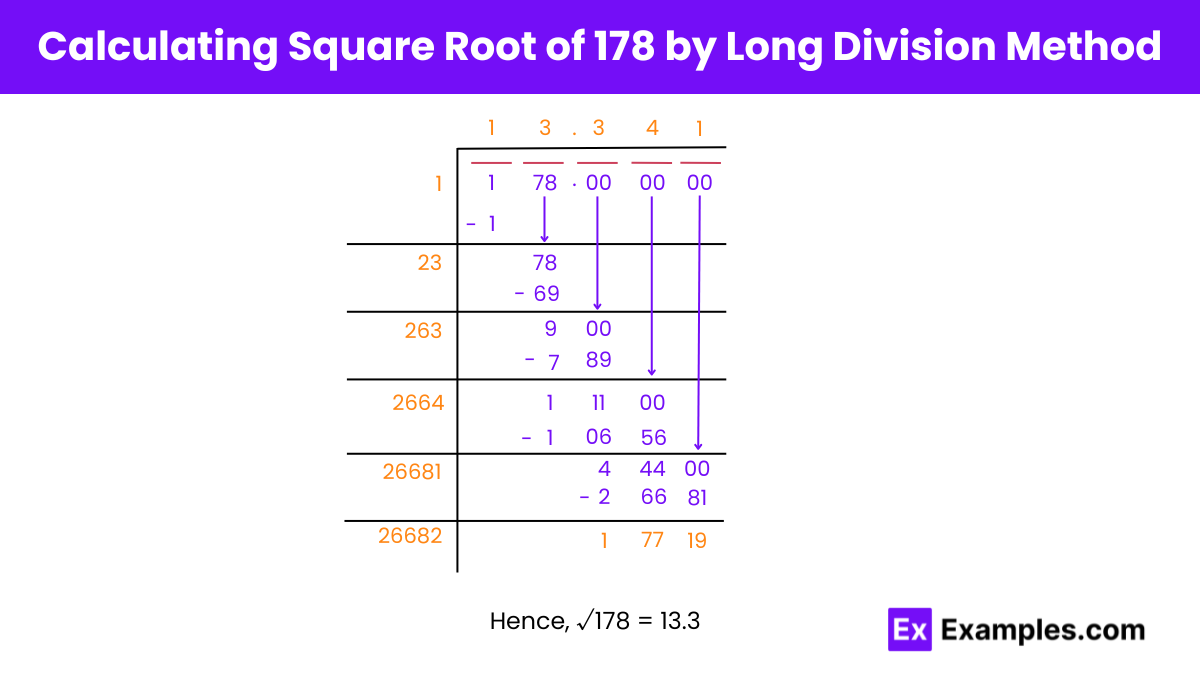
Certainly, here are the steps rewritten with subheadings:
Finding the Square Root of 178 by Long Division Method
Step 1: Grouping Digits
Form pairs: 01 and 78.
Step 2: Finding Initial Quotient
Find a number Y (1) such that its square is less than or equal to 01. Divide 01 by 1, resulting in a quotient of 1.
Step 3: Bringing Down the Next Pair
Bring down the next pair 78, to the right of the remainder 0. The new dividend becomes 78.
Step 4: Forming the New Divisor
Add the last digit of the quotient (1) to the divisor (1), yielding 2. Find a digit Z (which is 3) such that 2Z × Z is less than or equal to 78. Together, 2 and Z (3) form a new divisor 23 for the new dividend 78.
Step 5: Dividing and Finding Remainder
Divide 78 by 23 with the quotient as 3, resulting in a remainder of 9.
Step 6: Decimal Places
Continue the process to find decimal places after the quotient 13. Bring down 00 to the right of this remainder 9, making the new dividend 900.
Step 7: Repeating the Process
Repeat the above steps for finding more decimal places for the square root of 178.
Conclusion: Approximation
Therefore, the square root of 178 by the long division method is approximately 13.3.
178 is Perfect Square root or Not?
No, 178 is not a perfect square.
To determine if 178 is a perfect square, we need to find its square root.
The square root of 178 is a decimal number, approximately 13.341664, which means 178 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. Since the square root of 178 is not an integer, 178 is not a perfect square.
FAQS
Can the square root of 178 be simplified?
No, the square root of 178 cannot be simplified further into a simpler radical or fraction. It is an irrational number.
How is the square root of 178 represented in mathematical notation?
The square root of 178 is represented as √178.
What are some real-world applications of the square root of 178?
The square root of 178 can be used in various mathematical and scientific calculations, such as in geometry, physics, engineering, and finance.
What are the properties of the square and square root of 178?
The square of 178 is a positive integer, while the square root of 178 is an irrational number. The square root of 178 is approximately 13.3417.
Share :
Practice Test
Which of the following is the square of the number closest to the square root of 178?
169
182
144
196
of 10
The square root of 178 can be expressed as which of the following irrational numbers?
√176
√181
√178
√169
of 10
If the square root of 178 is represented as √178, what is √178 squared?
178
356
358
400
of 10
What is the result of multiplying the square root of 178 by itself?
123
178
13.41
13.25
of 10
If a number's square root is approximately 13.41, what is the approximate value of the number itself?
169
172
178
196
of 10
How does the square of the square root of 178 compare to the number itself?
It is half of the number.
It is twice the number.
It is the same as the number.
It is smaller than the number.
of 10
Which number squared is closest to 178?
13
14
15
16
of 10
What is the principal square root of 178?
13.25
-13.41
13.41
13
of 10
If √178 is approximated to 13.4, what is the approximate value of √178 squared?
178.00
13.40
13.41
13.00
of 10