Square & Square Root of 180 – Examples, Methods, Calculation

In the realm of mathematics, particularly within algebra, squares and square roots are foundational. Squaring, demonstrated by multiplying a number like 180 by itself to yield 32400, is fundamental. This operation lays the groundwork for exploring properties of rational and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns, vital in algebraic studies and beyond. Squares and square roots serve as cornerstones in algebra, shedding light on the properties of rational and irrational numbers. Mastery of these fundamentals enhances one’s grasp of mathematical relationships and patterns, contributing to a deeper understanding of algebraic concepts and their applications across various mathematical domains.

Square of 180

A square number, like 180, results from multiplying an integer by itself. The square of 180 equals 32,400. This fundamental operation illuminates algebraic principles, showcasing the inherent properties of rational and irrational numbers, enriching understanding of mathematical relationships and patterns within algebraic studies.

Square Root of 180

The square root of 180, a non-square number, is an irrational number approximately equal to 13.416. Understanding square roots involves finding the number that, when multiplied by itself, equals 180. Mastery of square roots unveils fundamental mathematical concepts, essential for exploring algebraic relationships and patterns.

Is the Square Root of 180 Rational or Irrational?

The square root of 180 is irrational. It cannot be expressed as a fraction of two integers, and its decimal representation continues infinitely without repeating. Thus, it falls under the category of irrational numbers.

Rational Number:
A rational number is a fraction of two integers, with a non-zero denominator, expressed as a/b, where a and b are integers. Examples include 3/4, -5/2, 0, 1, -2, etc.

Example: 3/4 is rational as it’s a fraction with both numerator and denominator as integers, and the denominator isn’t zero.

Irrational Number:
An irrational number cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating. Examples include √2, π, and φ.

Example: √2’s decimal expansion is approximately 1.41421356…, non-repeating and infinite, hence it’s irrational.

Method to Find Value of Root 180

One method to find the square root of 180 is using the long division method. Here’s a simplified explanation of the steps:

Pair the digits of 180 starting from the decimal point, and place a bar over the pair.

Find the largest digit ‘x’ such that x × x is less than or equal to 180. This gives the first digit of the square root.

Subtract the square of the obtained digit from the pair of digits, and bring down the next pair of zeros.

Double the first digit to form a partial divisor and find the next digit of the square root by trial and error, ensuring the product of the new partial divisor and the new digit does not exceed the remainder.

Repeat step 4 until the desired level of accuracy is achieved.

Alternatively, you can use approximation methods or a calculator to find the square root of 180 efficiently.

Square Root of 180 by Long Division Method

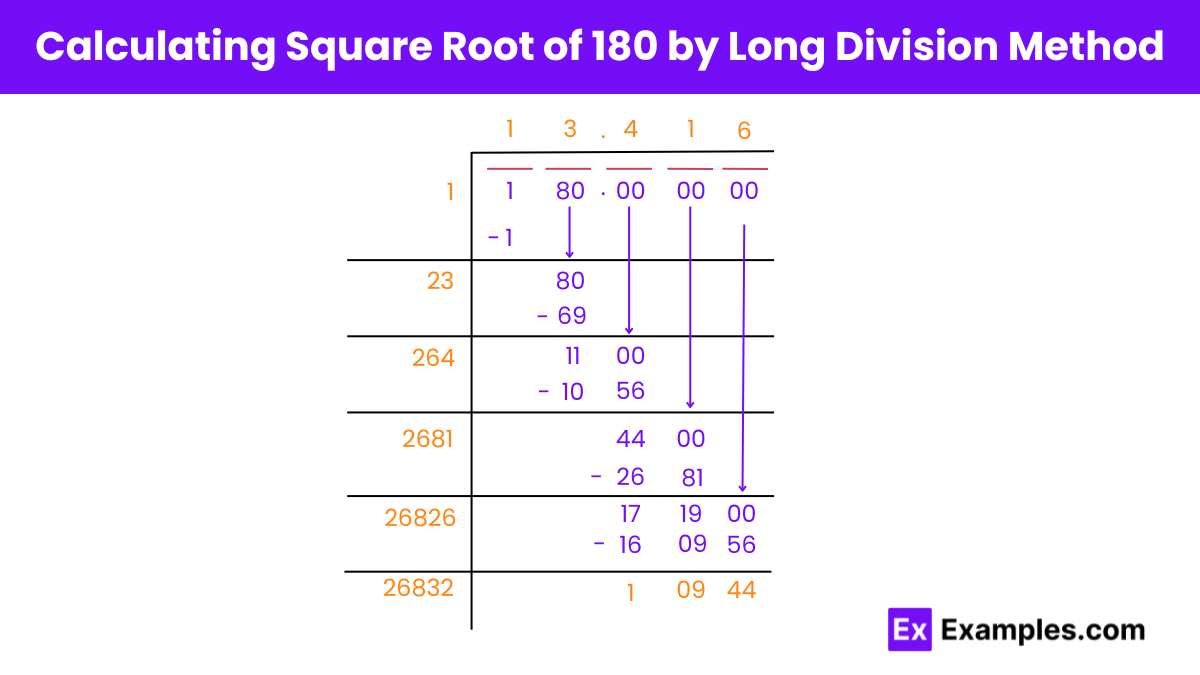
Long Division Method for Finding the Square Root of 180

Step 1: Setting Up
Express 180 as 180.000000. Group the digits into pairs from the right: 80 as a pair and 1 standing alone.

Step 2: Initial Quotient
Find a quotient equal to the divisor. 1 × 1 = 1. Multiply the quotient by the divisor and subtract from 1.

Step 3: Doubling the Quotient
Double the quotient obtained in step 2 to get 2, which becomes the new divisor. Bring down 80 as a pair to form the new dividend.

Step 4: Finding the Next Digit
Find a digit to add to the quotient such that when multiplied by the new divisor, the product is less than or equal to 80. Determine 23 × 3 = 69. Subtract from 80 to get a remainder of 11.

Step 5: Decimal Placement
Place a decimal point after the quotient ’13’ and bring down two zeros to form the new dividend, which becomes 1100. The new divisor is 13× 2 = 26x.

Step 6: Iterative Division
Continue finding digits to add to the quotient and subtracting from the dividend until reaching the desired level of precision, typically three decimal places.

Step 7: Final Result
Repeat the process until obtaining the desired number of decimal places in the quotient. Thus, the square root of 180 is approximately 13.416.

180 is Perfect Square root or Not?

180 is not a perfect square because it cannot be expressed as the square of an integer. In other words, there is no integer ‘n’ such that n × n equals 180. Therefore, 180 does not have an exact integer square root.

FAQs

What are some properties of the square and square root of 180?

The square of 180 is a positive integer, while the square root of 180 is a positive irrational number.

How do I verify if my calculation of the square root of 180 is correct?

You can verify your calculation by squaring the square root value obtained. If the result is 180, then your calculation is correct.

What are some real-life applications of understanding squares and square roots?

Understanding squares and square roots is essential in various fields such as engineering, physics, computer science, and finance for tasks like calculating areas, distances, and determining quantities.

Is there a pattern in the digits of the square root of 180?

The decimal representation of the square root of 180 is non-repeating and non-terminating, indicating no discernible pattern in its digits.

How does knowing the square and square root of 180 contribute to my understanding of algebraic concepts?

Understanding squares and square roots serves as a foundational step in algebra, helping to comprehend concepts like equations, inequalities, and polynomial functions.