Square & Square Root of 216
Square & Square Root of 216
Within the domain of mathematics, particularly in algebraic studies, the foundational principles of squares and square roots are pivotal. Squaring a number, such as 216, involves multiplying it by itself, resulting in 46656, a fundamental operation crucial in exploring the properties of both rational and irrational numbers. Understanding these concepts enriches comprehension of mathematical relationships and patterns. Mastery of these fundamentals is essential for navigating complex algebraic equations, where squares and square roots frequently emerge, illuminating the intricacies of numerical relationships within the framework of fractions and integers.
Square of 216
A square number, like 216, is the product of multiplying a number by itself. The square of 216 equals 46,656. In mathematics, understanding square numbers illuminates concepts such as area in geometry and serves as a foundational step in exploring algebraic expressions and equations.
Square Root of 216
Or
√216 = 14.696 Upto3 decimals
The square root of 216, approximately 14.6969, represents the number that, when multiplied by itself, equals 216. In mathematics, comprehending square roots reveals fundamental relationships between numbers and aids in solving equations and problems involving area, volume, and other geometric and algebraic concepts.
Square Root of 216: 14.6969384567
Exponential Form: 216^½ or 23^0.5
Radical Form: √216
Is the Square Root of 216 Rational or Irrational?
The square root of 216 is irrational. It cannot be expressed as a simple fraction of two integers. Instead, it is a non-repeating, non-terminating decimal.
Methods to Find Value of Root 216
There are several methods to find the value of the square root of 216:
Prime Factorization Method: Decompose 216 into its prime factors (2³ × 3³). Then, take the square root of each prime factor and multiply them together: √(2³ × 3³) = 2 × 3√2 = 6√2.
Long Division Method: This involves a step-by-step division process similar to long division but for square roots. It’s a bit more complex but provides an accurate result.
Using a Calculator: Most scientific calculators have a square root function that can directly provide the square root of 216 as approximately 14.6969.
Estimation Method: By knowing the square roots of nearby perfect squares, you can estimate the square root of 216. For example, 216 is between 196 (14²) and 225 (15²), so the square root of 216 is between 14 and 15.
Choose the method that suits your preference and the level of precision required.
Square Root of 216 by Long Division Method
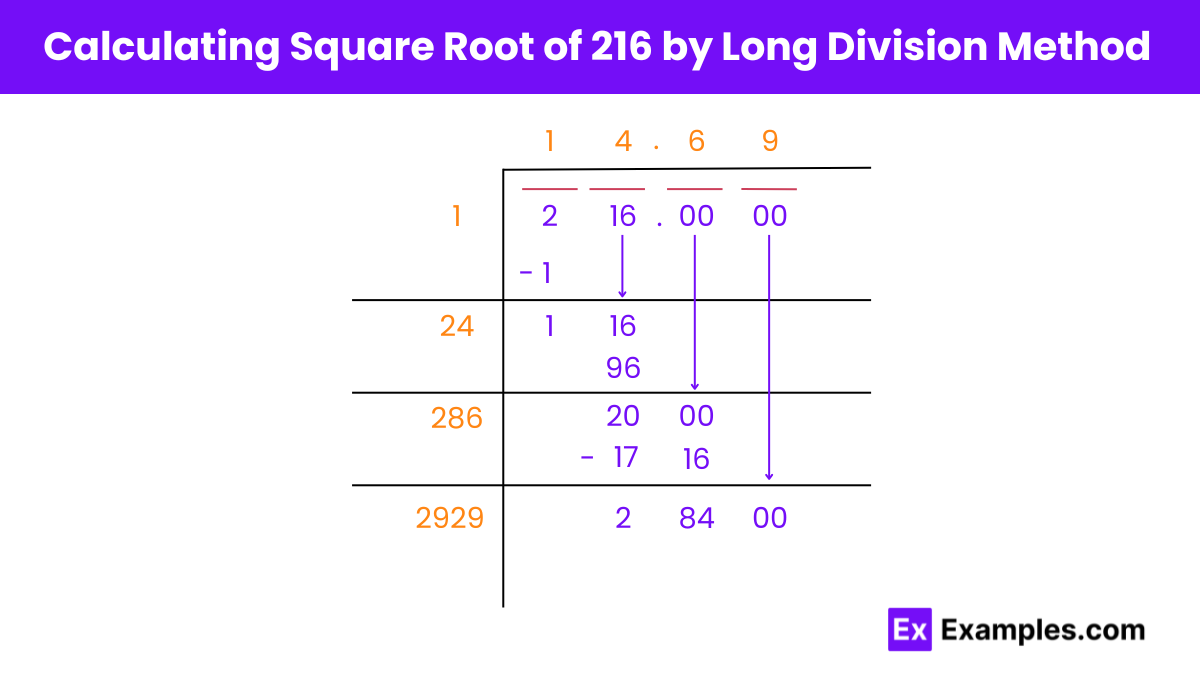
Sure, here’s a breakdown of finding the square root of 216 using the long division method with step-by-step headings:
Step 1: Pairing Digits
Starting from the right, group the digits of 216 in pairs. Place a bar above 16 and 1 separately, and pair the 0s in decimals in pairs of 2 from left to right.
Step 2: First Digit Estimation
Find a number that, when multiplied by itself, gives a product less than or equal to 2. This will be 1, so place 1 in the quotient and calculate the remainder.
Step 3: Update Divisor and Quotient
Drag down 16 beside the remainder. Also, add the divisor to itself and write it below.
Step 4: Second Digit Estimation
Find a number that, when added to the current divisor and multiplied by itself, results in a product less than or equal to 116. In this case, it’s 4. Update the divisor and quotient accordingly.
Step 5: Iteration for Decimal Places
Continue the process by repeating steps 3 and 4 to get additional decimal places if desired.
Step 6: Repeat Iteration
Repeat steps 3 to 5 until the desired level of precision is achieved.
Is 216 Perfect Square root or Not
No, 216 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. Since there is no integer value that, when multiplied by itself, equals 216, it is not a perfect square.
FAQ’S
How do you approximate the square root of 216 without a calculator?
You can use estimation methods or mental math techniques, such as finding the square roots of nearby perfect squares or using patterns in the digits.
What is the significance of the square root of 216 in geometry?
The square root of 216 can be used to find the length of the diagonal of a cube with side length 216, aiding in calculations related to volume, surface area, and spatial relationships.
Is there a pattern in the digits of the square root of 216?
While there isn’t a simple repeating pattern, the digits of the square root of 216 exhibit certain properties and relationships that mathematicians study, such as the distribution of prime factors.
Can the square root of 216 be expressed as a fraction?
No, the square root of 216 cannot be simplified into a fraction. It is an irrational number, meaning it cannot be expressed as a ratio of two integers.
How can the square root of 216 be used in real-life scenarios?
The square root of 216 can be applied in fields such as engineering, physics, and finance for calculations involving measurements, proportions, and rates of change.
Share :
