Square & Square Root of 252 – Methods , Calculations , Examples
In mathematics, particularly in algebra, understanding the concepts of squares and square roots is vital. When you square the number 252, by multiplying it by itself, it results in 63504. This action explores the nature of whole numbers and paves the way for investigating more complex mathematical relationships and patterns. Such exploration is crucial for enhancing our grasp of sophisticated mathematical concepts and theories.
Square of 252
252²(252 × 252) = 63504
The square of 252 refers to the result of multiplying the number 252 by itself. In mathematical terms, this is represented as 252². When you calculate 252 squared, it equals 63504. Squaring a number is a basic arithmetic operation used frequently in various mathematical calculations to determine area, formulate equations, and analyze data, among other applications.
Square Root of 252
√252= 15.874507
Or
√252= 15.874 Upto 3 decimals
The square root of 252 refers to the number that, when multiplied by itself, results in 252. Mathematically, this is expressed as √252. The value of the square root of 252 is approximately 15.87. Understanding square roots is important for solving quadratic equations, understanding geometric concepts, and analyzing real-world scenarios that involve area and other measurements.
Square Root of 252: 15.874507
Exponential Form of 252: (252)¹/² or (252)⁰.⁵
Radical Form of 252: √252
Is the Square Root of 252 Rational or Irrational?
The square root of 252 is irrational number
Rational:
The square root of 252 is not rational. Rational numbers are those that can be expressed as a fraction 𝑝/𝑞, where 𝑝 and 𝑞 are integers and 𝑞≠0. For a number to have a rational square root, all the prime factors in its prime factorization must have even exponents.
Irrational:
The square root of 252 is irrational number because it cannot be expressed as a fraction with integer numerator and denominator. The prime factorization of 252 is 2²×3²×7. The presence of the prime number 7 raised to an odd power (1) in the factorization ensures that the square root will be a non-repeating, non-terminating decimal, which is characteristic of irrational numbers.
Methods to Find the Value of Root 252
Finding the square root of 252 can be approached through various mathematical methods, suitable for different situations and tools available. Here are some commonly used methods:
1. Prime Factorization
- Factorize 252 completely into its prime factors: 252=2²×3²×7
- Since the prime factorization includes an odd exponent (7^1), the square root will be irrational.
- However, to approximate, you can simplify: √252=√2²×3²×7=6√7
2. Using a Calculator
- The quickest and most accurate way to find the square root of 252, especially when an exact fractional form isn’t easily achievable, is to use a calculator. This will provide the decimal approximation, which is about 15.87.
3. Estimation
- You can estimate the square root by identifying squares that are close to 252. For instance, 15²=225 and 16²=256. Since 252 is closer to 256, you can estimate the square root of 252 is slightly less than 16.
4. Numerical Methods (Newton’s Method)
- For a more precise calculation without a calculator, Newton’s method (or the method of approximations) can be applied. This involves an iterative formula: 𝑥𝑛₊₁=1/2(𝑥ₙ+252/𝑥ₙ), starting with a guess close to the actual square root (e.g., start with 15 or 16).
5. Exponent Rules
- If dealing with powers and roots in algebra, the exponential forms can be useful. Recognize 252 in terms of its prime factors, apply the square root to each factor, and simplify as much as possible.
Each method offers a pathway to understanding how the square root of 252 can be calculated or approximated, depending on the resources and level of precision required.
Square Root of 252 by Long Division Method
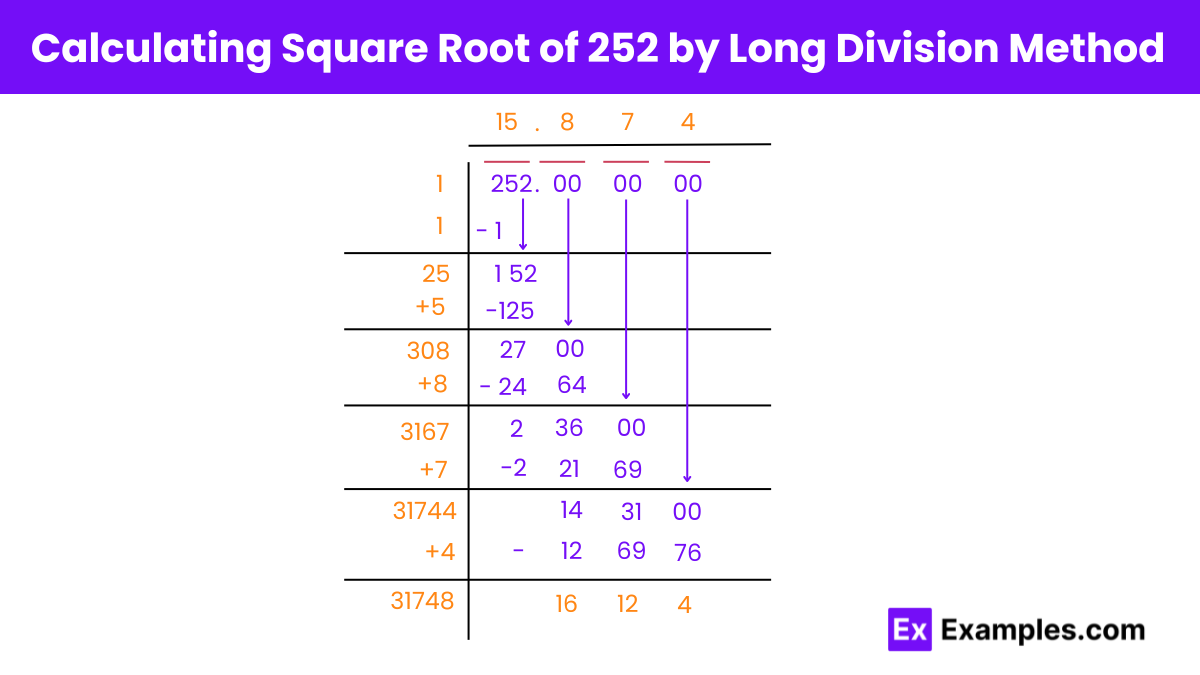
To find the square root of 252 using the long division method, follow these steps, which are ideal for manual calculation:
- Set up the number: Arrange the digits of 252 in pairs from right to left. Since it’s a three-digit number, you will have one pair and one single digit: 2 | 52.
- Find the largest square less than or equal to the first digit: The largest perfect square less than or equal to 2 is 1 (1²=1), so place 1 as the divisor and the beginning of your quotient above the pair.
- Subtract and bring down the next pair: Subtract 1 from 2, giving you a remainder of 1. Bring down the next pair of digits (52) to make it 152.
- Double the quotient: Double the current quotient (1), making it 2. This number (20 when considered as 20X) will be part of your new divisor.
- Find the next digit of the quotient: Look for a digit 𝑋 to place next to 2 in the quotient (forming 2X) and as the last digit in the divisor (20X + X), such that (20𝑋+𝑋)²≤152. X is found to be 5, since 25×5=125 fits best without exceeding 152.
- Subtract and continue if necessary: Subtract 125 from 152 to get a remainder of 27. Since we reach a reasonably close approximation and cannot bring down more digits, the process concludes.
252 is Perfect Square root or Not?
No, 252 is not a perfect square
No, 252 is not a perfect square. A number is considered a perfect square if it can be expressed as the square of an integer. The square root of 252 is approximately 15.87, which is not an integer. This indicates that there is no whole number that, when squared, equals 252. Thus, 252 does not meet the criteria to be classified as a perfect square.
FAQS
Can the square root of 252 be simplified further than 15.87?
While 15.87 is a decimal approximation, the square root can also be expressed in simplified radical form as 6√7.
Is the square root of 252 used in constructing geometric shapes?
Yes, understanding the square root of 252 can be crucial in constructing shapes where the dimensions or area calculations are related to this value.
How does the square root of 252 help in understanding quadratic equations?
In quadratic equations, calculating the square root of constants like 252 can be crucial for solving the equations, especially in completing the square or using the quadratic formula.
How is the number 252 used in statistics?
In statistics, 252 can be used to determine sample sizes for experiments, calculate degrees of freedom in chi-square tests, or as part of annual data analysis since there are typically 252 trading days in a financial year.
What is the square factor of 252?
The square factor of 252, derived from its prime factorization 252=2²×3²×7, is 36. This is the largest perfect square ( 2²×3²=4×9 ) that divides 252 evenly.



