Square & Square Root of 288
Square & Square Root of 288
In the domain of mathematics, especially within algebra, squares and square roots hold paramount importance. They serve as the cornerstone upon which our comprehension of rational and irrational numbers is built. By considering a number like 288 and squaring it, we unveil the fundamental essence of this operation, facilitating a deeper exploration of mathematical relationships and patterns.
Square of 288
A square number, such as 288, arises from multiplying an integer by itself. The square of 288 equals 82,944, showcasing algebraic principles and enriching our understanding of mathematical relationships and patterns within algebraic studies and beyond.
Square Root of 288
or
√288 ≈ 16.970 upto 3 decimals
The square root of 288, a perfect square number, is approximately 17. Mastering square roots involves identifying the number that, when multiplied by itself, equals 288. This understanding is crucial for exploring algebraic relationships and patterns within mathematics.
Exponential Form: 288^1/2 or 288^0.5
Radical Form: √288
Is the Square Root of 288 Rational or Irrational?
Rational Numbers: Rational numbers are expressible as fractions of two integers.
Irrational Numbers: Irrational numbers cannot be expressed as fractions of integers.
Since the square root of 288 is a perfect square, it is rational. It can be expressed as the fraction 17/1.
Methods to Find the Value of Root 288
Estimation Method: Begin with an initial approximation and refine it iteratively using methods like Newton-Raphson.
Prime Factorization Method: Express 288 as a product of prime factors, then find the square root of each prime factor.
Calculator: Utilize a calculator with a square root function to directly compute the square root of 288.
Square Root of 288 by Long Division Method
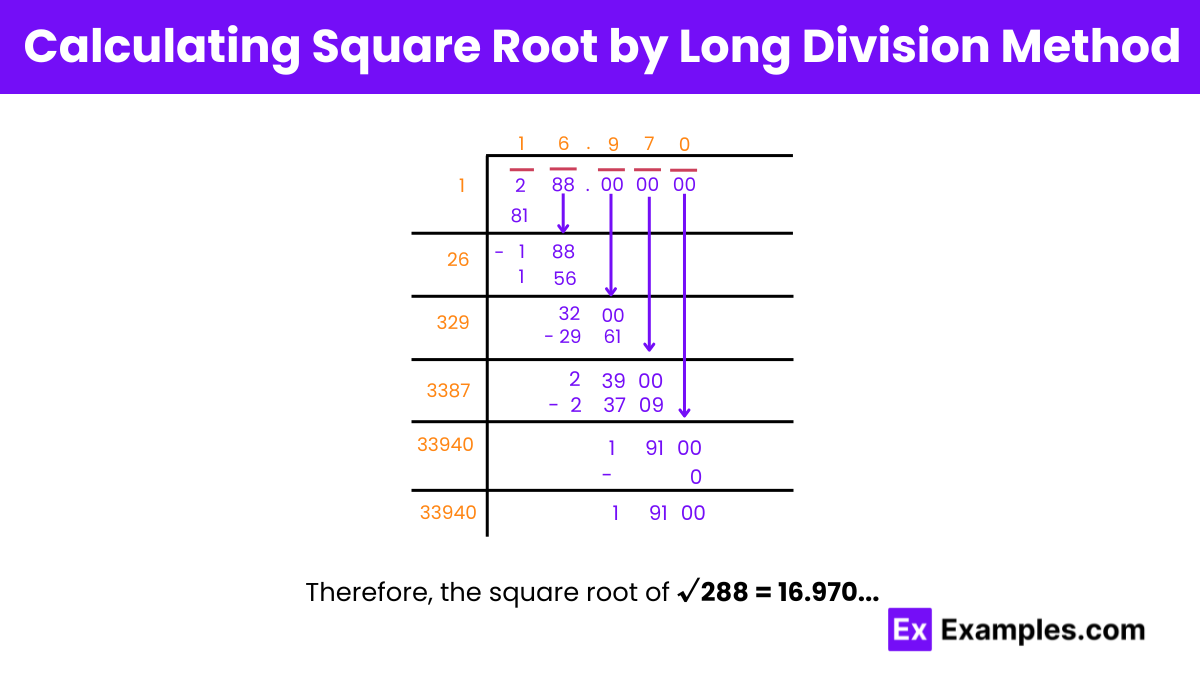
Step 1: Pair the digits of the number starting from the one’s digit. 288 has 3 digits. Pair 88 by placing a bar over them.
Step 2: Find a number such that its square is less than or equal to the first pair from the left side (2). Subtract the square (1) from the first pair and add the next pair (88) as the divisor.
Step 3: Take double the quotient (1) and place a digit with the divisor such that their product is less than the dividend. Add a number (6) with 2 to form 26, whose square is 156. Subtract from 188, resulting in 32.
Step 4: Take double the quotient (26) and place a digit with the divisor, adding a pair of zeros to the original dividend. Multiply 329 by 9, yielding 2961. Subtract from 18800, giving 191.
Step 5: Repeat the process, taking double the quotient (169) as a divisor and adding a digit (7). Multiply 3387 by 7, resulting in 23709. Subtract from 19100, yielding 191.
Step 6: Continue the process iteratively until the desired level of accuracy is achieved.
288 is a Perfect Square or Not
288 is not a perfect square because it cannot be expressed as the product of an integer multiplied by itself. In other words, there are no integers where the product of the integer with itself equals 288.
How to convert 288 into perfect square number?
To convert 288 into a perfect square number, multiply it by a factor that will result in a perfect square. For instance, multiplying 288 by 4 yields 1152, a perfect square.
What is 288 cube square root?
The cube root of 288 is approximately 6.879, as it is the number that, when multiplied by itself twice, equals 288.
Is the square root of 288 an integer?
No, the square root of 288 is not an integer. It is approximately 17, which is not a whole number.
What are the factors of 288
The factors of 288 include 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, and 288.
Share :
