Square & Square Root of 3600 – Methods, Calculation, How to find

In algebra, squares and square roots are indispensable, serving as keystones in myriad calculations and analyses. They unlock deeper insights into numerical systems, bridging the realms of rationality and irrationality. Mastery of these fundamentals empowers mathematicians to navigate complexities, from basic arithmetic to advanced equations, fostering a holistic understanding of mathematical principles. Thus, the study of squares and square roots transcends mere computation, evolving into a profound exploration of mathematical structure and logic.

Square of 3600

A square number results from multiplying an integer by itself. The square of 3600 is 12,960,000. In mathematics, square numbers exhibit distinct properties, crucial for understanding algebraic relationships and patterns. Exploring the square of 3600 unveils fundamental principles, enriching comprehension of mathematical structures and operations.

Square Root of 3600

The square root, a fundamental concept in mathematics, reveals the number that, when multiplied by itself, yields the original number. The square root of 3600 is 60. Understanding square roots elucidates the properties and relationships underlying numbers, offering insights into the square of 3600 and its mathematical significance.

Is the Square Root of 3600 Rational or Irrational?

Rational numbers are numbers that can be expressed as the quotient of two integers, where the denominator is not zero

Irrational numbers are numbers that cannot be expressed as the quotient of two integers. Their decimal expansions are non-terminating and non-repeating.

Methods to Find Value of Root 3600.

1. Prime Factorization Method:

• Factorize 3600 into its prime factors:
  3600 = 2⁴ × 3² × 5²
• Take the square root of each factor:
  √3600 = √2⁴ × 3² × 5²
• Simplify by taking the square root of each component:
  √2⁴ = 2² = 4
  √3² = 3
  √5² = 5
• Multiply the results:
  [ 4 × 3 × 5 = 60 ]
  Therefore, (√3600 = 60 ).

2. Long Division Method:

• Group the digits in pairs from right to left (36 and 00).
• Find the largest number whose square is less than or equal to 36 (which is 6):
  [ 6 × 6 = 36 ]
• Subtract and bring down the next pair of digits (00), making it 0000.
• Double the quotient (6), giving us 12, and find a digit (0) to place next to 12 to complete the square root process. This method shows that:
  [√3600 = 60 ]

3. Using a Calculator:

• Simply input 3600 and press the square root (√) button.
• The display will show 60.

Square Root of 3600 by Long Division Method

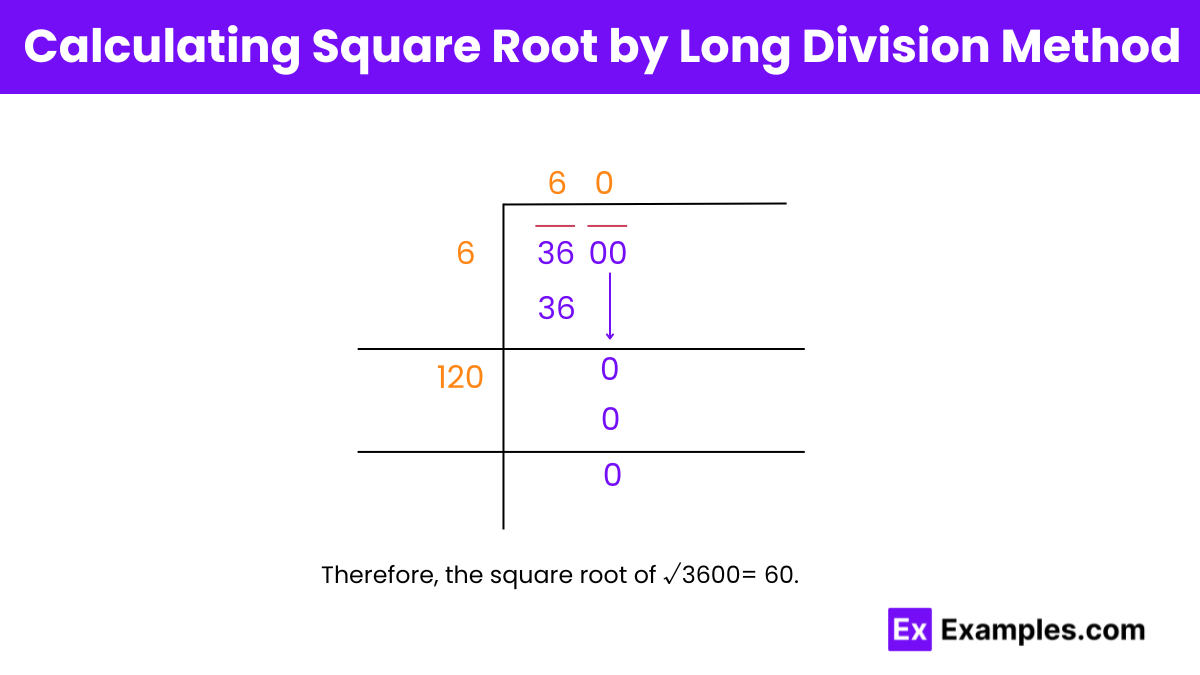
Step 1: Form pairs: 36 and 00.

Step 2: Find a number Y (6) such that its square is less than or equal to 36. Divide 36 by 6, resulting in a quotient of 6.

Step 3: Bring down the next pair, 00, to the right of the remainder 0, making the new dividend 0.

Step 4: Add the last digit of the quotient (6) to the divisor (6), giving 12. To the right of 12, find a digit Z (which is 0) such that (12Z × Z ≤ 0). After finding Z, 12 and Z (0) together form a new divisor, 120, for the new dividend, 0.

Step 5: Divide 0 by 120, with the quotient as 0, resulting in the remainder (0 – 120 × 0 = 0 – 0 = 0).

3600 is Perfect Square root or Not

A perfect square is a number that is the square of an integer. In the case of 3600, it is the square of the integer 60.

FAQs

What is the prime factorization of 3600?

The prime factorization of 3600 is ( 2⁴ × 3² × 5² ). This represents 3600 as the product of its prime factors raised to their respective powers.

Can the square root of 3600 be simplified further?

No, the square root of 3600 is already in its simplest form as an integer, 60

Can 3600 be expressed as the sum of consecutive square numbers?

Yes, 3600 can be expressed as the sum of consecutive square numbers. For example, 3600=592²+612²