What is the square of 51?
2601
1024
2550
2600
of 10
Square & Square Root of 51 – Examples, Methods, Calculation
Square & Square Root of 51 – Examples, Methods, Calculation
Square of 51
A square number, such as 51, results from multiplying an integer by itself. The square of 51 equals 2,601. This fundamental operation illustrates algebraic principles, showcasing the inherent properties of rational and irrational numbers, enriching understanding of mathematical relationships and patterns within algebraic studies.
Square Root of 51
The square root of 51, an irrational number, is approximately 7.14142842854285. Understanding square roots involves finding the number that, when multiplied by itself, equals 51. Mastery of square roots unveils fundamental mathematical concepts, essential for exploring algebraic relationships and patterns within the realm of mathematics.
Is the Square Root of 51 Rational or Irrational?
This means it cannot be expressed as a simple fraction, and its decimal representation is non-repeating and non-terminating.
A rational number can be expressed as the quotient of two integers, where the denominator is not zero.
An irrational number cannot be expressed as a fraction of two integers, and its decimal representation is non-repeating and non-terminating.
Methods to Find Value of Root 51
1. Prime Factorization Method
- Express 51 as a product of its prime factors.
- Simplify the expression by pairing the factors, then find the square root.
2. Long Division Method
- Use long division to approximate the square root of 51.
3. Using a Calculator
- Input √51 into a scientific calculator to obtain an approximation of the square root.
4. Newton’s Method (Iterative)
- Start with an initial guess for the square root and use iterative formulae to refine the approximation.
5. Using a Table of Squares
- Refer to mathematical tables listing square roots of numbers and find the closest approximation for √51.
Square Root of 51 by Long Division Method
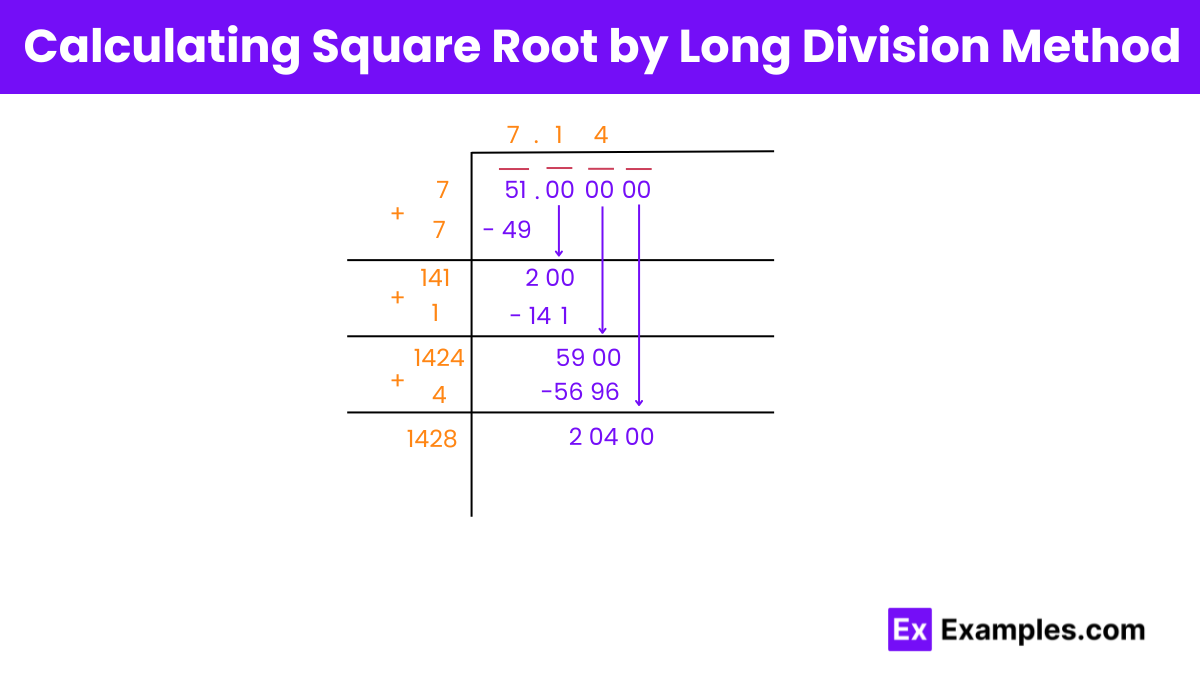
Step 1: Begin by grouping the digits of 51 in pairs, starting from the right, and include any decimals.
Step 2: Identify a number whose square is less than or equal to 51, like 7.
Step 3: Divide 51 by 7, resulting in a quotient of 7 and a remainder of 2.
Step 4: Bring down the next pair of digits (in this case, zeros) to the remainder to form the new dividend, 200.
Step 5: Double the divisor and append a variable, resulting in a new divisor. Determine the value of the variable that makes the product of the divisor and the variable less than or equal to the new dividend.
Step 6: Place the determined value in the quotient after the decimal point, and continue the process with the updated divisor.
Is 51 Perfect Square root or Not
A perfect square is a number that can be expressed as the product of an integer with itself. Since there is no integer (n) such that (n× n = 51), 51 is not a perfect square.
FAQs
Which value is closest to √51?
The two perfect squares surrounding 51 are (7² = 49) and (8² = 64). Since 51 lies closer to 49 than 64, the value closest to √51 is (7).
What is 51 cubed root?
The cube root of 51 is approximately equal to 3.707. This represents the number that, when multiplied by itself twice, equals 51.
Share :
Practice Test
What is the square root of 51 approximately?
7.1
7.5
7.3
7.8
of 10
Which of the following is the closest integer to the square root of 51?
6
7
8
9
of 10
If you square 51, what is the result?
2500
2550
2601
2700
of 10
What is the value of the square root of 51 to two decimal places?
7.14
7.12
7.11
7.10
of 10
How do you find the square of 51?
Multiply 51 by 52
Add 51 to itself
Multiply 51 by itself
Subtract 51 from 100
of 10
Which number squared gives a result closest to 51?
7
8
9
10
of 10
What is the result of 51 squared?
2601
2700
2500
2550
of 10
The square root of 51 lies between which two consecutive integers?
6 and 7
7 and 8
8 and 9
5 and 6
of 10
What is the approximate value of the square root of 51?
7.20
7.10
7.30
7.40
of 10