Square & Square Root of 512 – Examples, Methods, Calculation
In the field of mathematics, particularly in algebraic studies, understanding squares and square roots is crucial. Squaring a number involves multiplying it by itself, as seen when 512 is squared to produce 262144. This operation is essential for exploring the properties of both rational and irrational numbers. Rational numbers can be expressed as a fraction of two integers, whereas irrational numbers cannot be neatly expressed in fractional form. Mastering these basic concepts is vital for deepening one’s grasp of mathematical relationships and patterns, highlighting the significance of squares and square roots in algebraic investigations.
Square of 512
The square number of 512 is a square number calculated by multiplying 512 by itself, resulting in 262144. This square number exemplifies the fundamental concept of squaring in mathematics, showcasing the growth in magnitude when numbers are multiplied by themselves.
Square Root of 512
√512 = 22.627416998
Or
√512 = 22.627 Upto 3 decimals
The square root of 512 is a key concept in mathematics, determining the number that, when multiplied by itself, equals 512. Approximately 22.6274, this value is not a square number, highlighting the intricate relationship between numbers and their roots within algebraic studies.
Square Root of 512 : 22.627416998
Exponential Form : 512^½ or 512^0.5
Radical Form : √512
Is the Square Root of 512 Rational or Irrational?
The square root of 512 is irrational.
The square root of 512 is irrational. This is because it cannot be expressed as a simple fraction of two integers where both the numerator and the denominator are integers without any square factors other than the decimal form of the square root of 512 does not terminate or repeat, further confirming its irrational nature.
Rational Number:
A rational number is defined as a number that can be written as a fraction, where both the numerator and the denominator are integers, and the denominator is not zero. This is typically expressed in the form (a/b). Examples include numbers like 3/4, -5/2, 0, 1, and -2. For instance, 3/4 is a rational number because it has integers as its numerator and denominator, with the denominator non-zero.
Irrational Number:
An irrational number is one that cannot be expressed as a simple fraction of two integers. Its decimal form is both non-terminating and non-repeating. Notable examples of irrational numbers include (√2, π (pi), and φ (phi). For example, (√2) is irrational because its decimal expansion (approximately 1.41421356…) continues indefinitely without repeating.
Method to Find Value of Root 512
Finding the square root of 512 can be approached in several ways, depending on the tools and accuracy you need. Here’s a step-by-step guide to a couple of methods:
1. Estimation Method
This method involves using estimates and refining them:
- First, find two perfect squares between which 512 falls. For example, (22² = 484) and (23² = 529). So, (√512) is between 22 and 23.
- Estimate a middle value between 22 and 23, such as 22.5, and square it to see if it gets closer to 512. Adjust the estimate based on the result.
2. Using a Calculator
For most practical purposes, using a calculator is the easiest and fastest way to find the square root:
- Simply enter 512 and press the square root function √x to get an immediate decimal approximation.
3. Babylonian Method (or Heron’s Method)
This is an ancient algorithm for finding square roots, which uses iteration:
- Start with an initial guess (x_0). Given that 512 is between (22²) and (23²), you could start with (x_0 = 22.5).
- Use the formula (x_{n+1} = 1/2 (xₙ+512/xₙ) to generate better approximations. Repeat until the change between two successive iterations is within your required tolerance.
4. Using Prime Factorization
- Factor 512 into primes: (512 = 2⁹).
- Since the exponent is odd, 2⁹/² = 2⁴.⁵, which confirms the square root is irrational. However, this method also quickly shows that √512 = 2⁴.⁵ = 16 ×√2 ), which is a useful form for some mathematical purposes.
Each method has its pros and cons depending on whether you need a quick answer, a precise one, or a deeper understanding of the properties of the number.
Square Root of 512 by Long Division Method
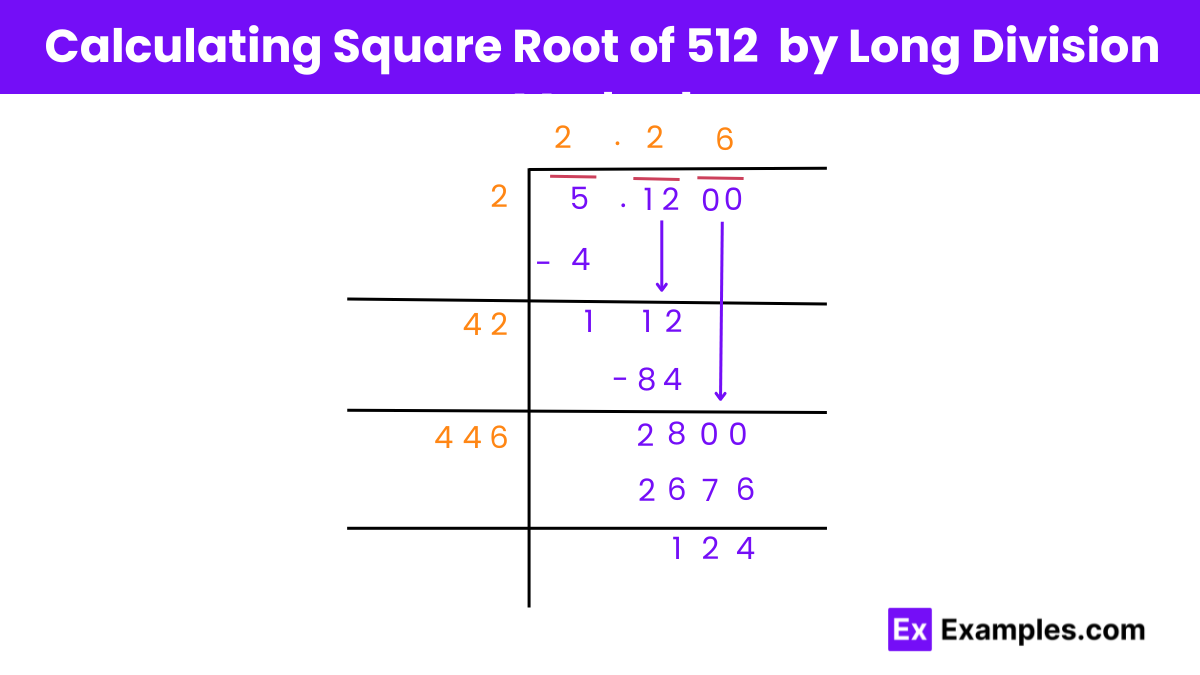
Finding the Square Root of 512 Using Long Division Method
Step 1: Pair the Digits
Group the digits of 512 into pairs from the right. You will have two pairs: ‘5’ and ’12’.
Step 2: Find the First Digit of the Quotient
Identify the largest number whose square is less than or equal to the first group (‘5’). Here, (2² = 4), so the first digit of your quotient is 2.
Step 3: Subtract and Bring Down the Next Pair
Subtract the square of your quotient from the first pair and bring down the next pair. The new dividend is now ‘112’ (from ‘5 – 4′ and ’12’ brought down).
Step 4: Update the Divisor and Find the Next Digit of the Quotient
Add the last quotient digit to the divisor (2 + 2 = 4). Append a digit (say ‘x’) to this sum (making it ‘4x’) such that when ‘4x’ is multiplied by ‘x’, the product is less than or equal to the new dividend ‘112’. ’42 × 2 = 84′ fits since 84 is less than 112. The next quotient digit is thus 2.
Step 5: Repeat with More Precision (if needed)
Continue the process with decimal precision if a more accurate value is desired. Bring down pairs of zeros, adjust the divisor as before, and determine subsequent digits in the quotient.
Step 6: Final Quotient
The quotient obtained through this method provides the approximate square root of 512, refining further as needed with decimals.
512 is Perfect Square root or Not?
No, 512 is not a perfect square.
No, 512 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. When you take the square root of 512, you get an irrational number, approximately 22.6274, which is not an integer. Therefore, 512 does not meet the criteria of a perfect square.
FAQs
What mathematical principles are demonstrated by squaring 512?
Squaring 512 demonstrates principles of exponential growth, which is fundamental in areas like algebra and geometry.
How does the square of 512 relate to powers of two?
The square of 512 (262,144) is itself a power of two, specifically 218218, which shows how exponential functions scale.
Can the square of 512 be broken down into simpler components or factors?
Yes, 262,144 can be factored into smaller powers of 2: 22×216=4×65,53622×216=4×65,536.
What is the significance of the square of 512 in digital computing?
In computing, understanding squares of numbers like 512 can be crucial for designing algorithms and understanding data storage capacities, especially since 512 bytes is a common block size in file systems.
How do mathematicians use the square of 512 in theoretical studies?
The square of 512 can be used in mathematical proofs and theoretical studies, particularly in exploring properties of numbers and their relationships.



