Square & Square Root of 58 – Methods , Calculations , Examples

In mathematics, especially within the domain of algebra, grasping the concepts of squares and square roots is essential. Squaring the number 58, by multiplying it by itself, results in 3364. This computation sheds light on the characteristics of whole numbers and serves as a foundation for probing into more intricate mathematical relationships and patterns. Engaging in such calculations is fundamental for deepening our understanding of advanced mathematical concepts and theories.

Square of 58

The square of 58 refers to the result of multiplying the number 58 by itself. Mathematically, this is expressed as 58×58. Squaring a number is one of the fundamental operations in arithmetic and algebra, serving as a key concept for developing more complex mathematical ideas. When you square 58, you obtain 3364. This calculation helps illustrate properties of exponents and powers, which are crucial for understanding advanced topics in mathematics such as quadratic equations, power functions, and polynomial identities.

Square Root of 58

The square root of 58 refers to the number that, when multiplied by itself, results in 58. Mathematically, this is expressed as √58. The exact square root of 58 is an irrational number, meaning it cannot be expressed as a simple fraction, and its decimal representation continues indefinitely without repeating. This concept is central in various branches of mathematics, including algebra and geometry, where understanding square roots is crucial for solving equations and calculating dimensions. The square root of 58, approximately 7.61577311, is particularly useful in real-world applications where precise calculations are necessary, such as in engineering and physics.

Is the Square Root of 58 Rational or Irrational?

Rational

No, the square root of 58 is not rational. Rational numbers are those that can be expressed as the ratio of two integers (where the denominator is not zero). The square root of 58, being an irrational number, does not meet this criterion as it cannot be precisely written as a simple fraction and its decimal expansion is non-terminating and non-repeating.

Irrational

Yes, the square root of 58 is irrational. Irrational numbers are defined by their non-terminating, non-repeating decimal expansions, which cannot be accurately represented as fractions. Since 5858​ does not result in a neat, fractional value and its decimal continues indefinitely without repeating, it is classified as irrational.

Methods to Find the Value of Root 58

Finding the value of the square root of 58 involves a few methods. Here are a couple of common ones:

1. Using a Calculator: The quickest and easiest method is to use a calculator that has a square root function. Simply input 58 and press the square root button to get the result. The square root of 58 is approximately 7.61577.
2. Manual Calculation: If you need to find the square root manually, you can use methods like the Babylonian method or long division. The Babylonian method involves making an initial guess and refining it through iterations until you reach a close approximation. Here’s a brief outline:
   • Step 1: Make an initial guess. For example, you can start with 7, as it’s close to the actual square root of 58.
   • Step 2: Divide the number you’re finding the square root of (58) by your initial guess (7).
   • Step 3: Average the result of the division with your initial guess.
   • Step 4: Repeat steps 2 and 3 until you reach a satisfactory level of precision.
   • After a few iterations, you’ll converge to an approximation of the square root of 58, which is approximately 7.61577.

Square Root of 58 by Long Division Method

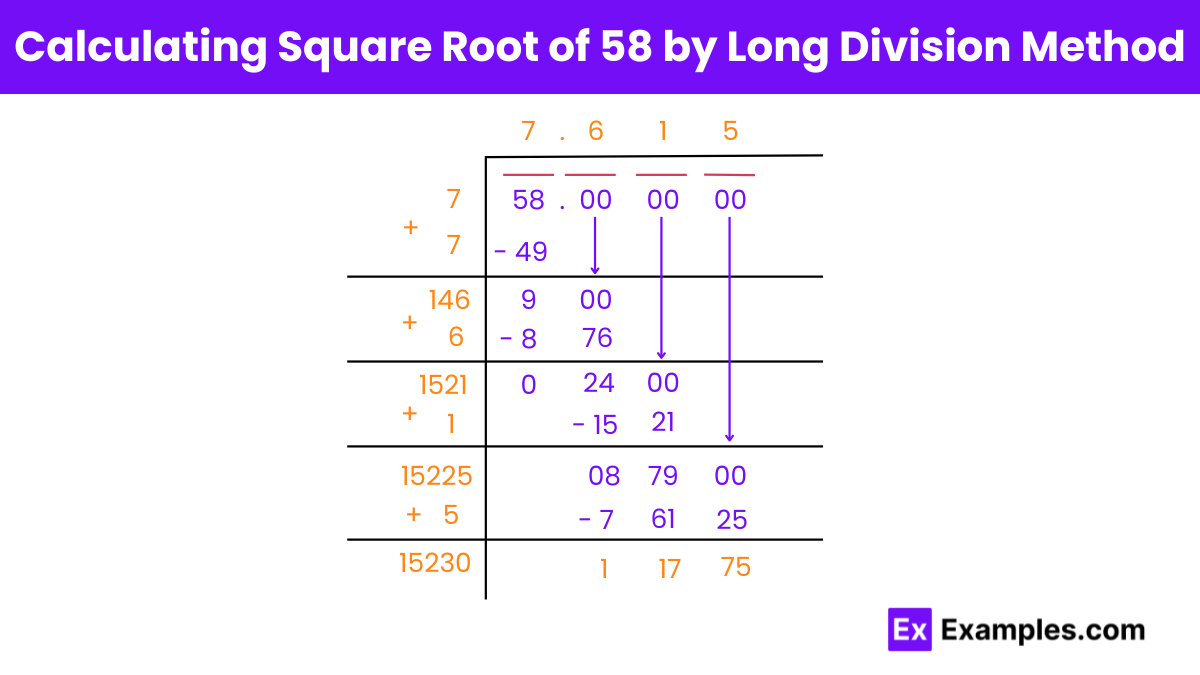
Finding the square root of 58 by long division method involves a series of steps. Here’s how you can do it:

1. Group the Digits: Group the digits of 58 into pairs, starting from the decimal point if there is one. Since 58 is a whole number, we’ll group the digits from right to left, starting with the units digit. So, in this case, we have one pair: 58.
2. Find the Largest Perfect Square: Find the largest perfect square that is less than or equal to the first group. The largest perfect square less than 58 is 49 (7 * 7).
3. Divide and Find Quotient: Divide the first group by this perfect square. In this case, 58 ÷ 49 = 1 with a remainder of 9.
4. Bring Down the Next Pair: Bring down the next pair of digits to the right of the remainder. Since there are no more digits, we’ll add a decimal point and a pair of zeros.
5. Double the Quotient: Double the quotient obtained in step 3 and write it as a tentative divisor.
6. Find the Next Digit of the Root: Find the largest digit ‘x’ such that (20 * (divisor + x)) * x is less than or equal to the number formed by the remainder and the next pair of digits brought down. Here, the number formed by the remainder and the next pair of digits brought down is 900.
7. Repeat: Repeat steps 3 to 6 until you have found the desired level of precision.

58 is Perfect Square root or Not?

No, 58 is not a perfect square. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 25 is a perfect square because it can be expressed as 5×5. However, 58 cannot be expressed as the product of an integer with itself, so it is not a perfect square.

FAQS

What is the significance of the square root of 58?

The square root of 58 is useful in various mathematical and scientific calculations, particularly in geometry, physics, and engineering. It represents the length of one side of a square with an area of 58 square units.

What is the square root of 58 rounded to the nearest whole number?

The square root of 58 rounded to the nearest whole number is 8.

How can the square root of 58 be represented on a number line?

The square root of 58 would be represented on a number line approximately between 7 and 8, closer to 8.

How does the square root of 58 compare to the square root of other numbers?

The square root of 58 is greater than the square root of any perfect square less than 58 and less than the square root of any perfect square greater than 58.