Square & Square Root of 625

In the realm of mathematics, particularly in algebra, understanding squares and square roots is essential. Squaring a number involves multiplying it by itself, as demonstrated with 625, which when squared results in 390,625. This operation delves into the properties of rational numbers and provides a basis for exploring more complex mathematical relationships and patterns, which are vital for gaining deeper insights into advanced mathematical concepts.

Square of 625

625²(625 × 625) = 390625

The square of 625 refers to the result of multiplying the number 625 by itself. In mathematical terms, squaring a number means raising it to the power of two. For 625, this calculation is expressed as 625², which equals 390,625. Squaring is a fundamental arithmetic operation that provides insights into various mathematical properties and is used across different areas of mathematics.

Square Root of 625

√625= 25

The square root of 625 refers to the number that, when multiplied by itself, results in 625. In mathematical notation, this is expressed as √625​. For 625, the square root is 25, since 25×25=625. Understanding square roots is a basic yet crucial concept in mathematics, helping to solve equations, understand geometric properties, and analyze data sets.

Square Root of 625: 25

Exponential Form of 625: 5^⁴

Radical Form of 625: √625

Is the Square Root of 625 Rational or Irrational?

The square root of 625 is rational number

Rational Number:

The square root of 625 is rational. A rational number is defined as a number that can be expressed as the fraction 𝑝𝑞​, where 𝑝 and 𝑞 are integers and 𝑞 is not zero. In this case, √625=25, which can be expressed as 25/1​, satisfying the conditions for rational numbers. Since 25 is a whole number, it clearly fits the definition of a rational number.

Irrational Number:

A number is considered irrational if it cannot be expressed as a simple fraction 𝑝𝑞 where both 𝑝 and 𝑞 are integers and 𝑞 is not zero. Irrational numbers have non-repeating, non-terminating decimal expansions. An example is √2​, which approximates to 1.41421356… and continues indefinitely without repeating. However, since √625=25 is a terminating decimal and can be expressed as a fraction, it is not irrational.

Methods to Find the Value of Root 625

Finding the square root of 625 can be done using various methods. Here are some methods are as follows:

1. Prime Factorization

• Decompose 625 completely into its prime factors.
• Since 625=5×5×5×5=5⁴
• Group the factors in pairs: (5×5)×(5×5)=25×25
• The square root of 625 is 25.

2. Using a Calculator

• This is the simplest and most direct method; simply input 625 into a calculator and press the square root function to obtain 25.

3. Estimation

• By knowing the squares close to 625 (such as 20^²=400 and 30^²=900), you can estimate that the square root of 625 lies between 20 and 30.
• Checking squares around the midpoint, such as 25^², confirms that 25 is the square root.

4. Exponent Rules

• Recognizing 625 as 5^⁴ and applying exponent rules ( √𝑥^²​=x),
• The even exponent 4 allows simplification using the rule √𝑎ᵇ=𝑎ᵇ/² giving 5^⁴/²=5^²​=25

These methods provide various ways to determine the square root of 625, each suited to different situations and levels of mathematical familiarity.

Square Root of 625 by Long Division Method

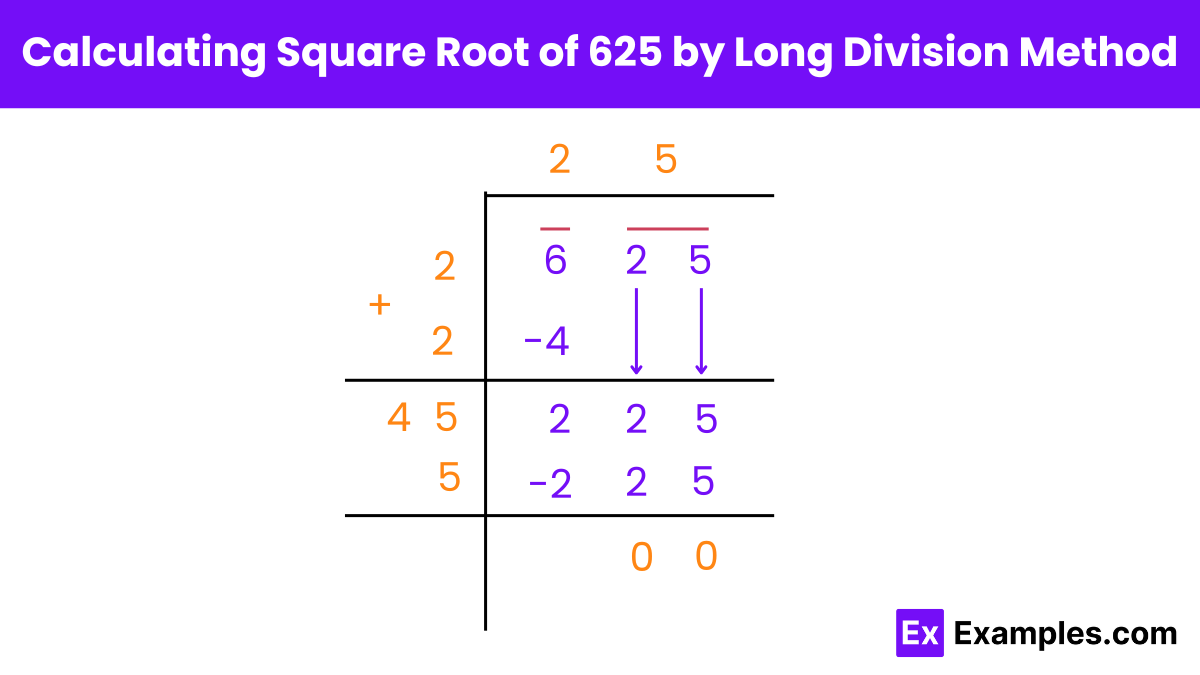
To find the square root of 625 using the long division method, follow these steps:

1. Pair the digits: Start by writing the number 625. Here, you only need to handle the three digits, so you pair them as 6, 25 from right to left.
2. Find the largest square: Look for the largest square less than or equal to the first pair or digit on the left, which is 6. The largest perfect square less than 6 is 4 (2²), so place 2 as the divisor above the first pair.
3. Subtract the square: Subtract 4 from 6, leaving a remainder of 2. Bring down the next pair of digits (25), making the number now 225.
4. Double the quotient: The initial quotient is 2. Double this to make 4. Place it beside the remainder to form a new dividend of 225.
5. Find the next digit: Find a digit 𝑋 that fits in the equation 40𝑋≤225 such that (20𝑋+𝑋)²≤225. 𝑋 will be 5, because 45×5=225.
6. Complete the calculation: Place 5 beside 2 in the quotient area, making the quotient 25. Subtract 225 from 225 to get a remainder of 0.

625 is Perfect Square root or Not?

Yes, 625 is a perfect square.

Yes, 625 is a perfect square. A perfect square is a number that can be expressed as the square of an integer. The integer whose square equals 625 is 25, since 25×25=625. Therefore, 625 fits the definition of a perfect square, with its square root being a whole number.

FAQS

What are the applications of knowing the square root of 625 in real life?

It can be used in various mathematical calculations, architectural designs, and when analyzing data sets that involve areas or other quadratic relations.

Is the square root of 625 used in geometry?

Yes, it is used in geometry to calculate side lengths of squares and is essential for determining areas and perimeters.

What mathematical operations involve the number 625?

Operations include finding its factors, multiples, square, and square root, which are useful in algebra and number theory.

How is the number 625 used in statistics?

In statistics, 625 can be used to calculate sample sizes, variance analyses, and in the construction of symmetric square matrices for complex data interpretations.

What is 4 root 625?

The fourth root of 625 is the number that, when multiplied by itself four times, equals 625. Mathematically, this is expressed as 4√625​. By breaking it down, since 625=5^⁴, the fourth root of 625 simplifies to 5 (5^⁴/⁴=5¹=5). Thus, the fourth root of 625 is 5. This calculation is an example of applying roots to simplify numbers exponentially.