Square & Square Root of 63 – Examples, Methods, Calculation

Square of 63

The square of 63 is 3,969. Squaring 63 entails multiplying it by itself, showcasing a fundamental mathematical operation. Understanding the properties of square numbers like 63 aids in comprehending mathematical concepts and relationships, contributing to a deeper understanding of numerical systems and their applications.

Square Root of 63

The square root of 63, an irrational number, is approximately 7.937253933193772. It represents the number that, when multiplied by itself, equals 63. Understanding square roots illuminates mathematical principles, offering insights into numerical relationships and facilitating problem-solving across various disciplines.

Is the Square Root of 63 Rational or Irrational?

This is because 63 is not a perfect square, meaning there are no integers that, when multiplied by themselves, equal 63. The square root of 63 is approximately 7.937253933193772, which cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. Thus, it is classified as an irrational number.

Rational numbers can be expressed as a fraction of two integers, where the denominator is not zero.

Irrational numbers cannot be expressed as a fraction and have non-repeating, non-terminating decimal expansions.

Methods to Find Value of Root 63

1. Prime Factorization Method

Find the Prime Factors:

• 63 = 3 × 3 × 7 = 3²×7

Express the Square Root:

• √63 = √3²×7= 3√7

Approximate the Value:

• Using the approximate value of √7≈2.645757​
• 3 × 2.64575 ≈ 7.93725

2. Long Division Method

Set Up the Long Division:

Group the digits in pairs from the decimal point outwards. For 63, it’s simply 63.000000…

Find the Largest Integer:

• Find the largest integer whose square is less than or equal to 63. This is 7 (since (7² = 49) and (8² = 64)).

Divide and Average:

• Start with an approximation (e.g., 7) and refine using:
• (7+ 63/7)/2= (7+9)/2= 8
• Repeat the process with 8, (8+63/8)/2= (8 + 7.875)/2 = 7.9375

Continue Refining:

• The more iterations you do, the closer you get to the precise value.

3. Using a Calculator

Direct Calculation:

• Use a scientific calculator to find√63.
• The result is approximately 7.937253933193772.

4. Newton’s Method (Iterative)

Initial Guess:

• Start with an initial guess, x₀. Let’s use 8.

Iterative Formula:

• Use the formula: xₙ₊₁ = 1/2(xₙ +63/xₙ)
• Iteratively apply the formula:
  • x₁ = 1/2 (8+63/8) = 7.9375
  • x₂= 1/2(7.9375 +63/7.9375) ≈ 7.937254
  • Continue until the desired accuracy is reached.

5. Using a Table of Squares

Reference Tables:

• Some mathematical tables list the square roots of numbers. Check the table for (\sqrt{63}).

Interpolate if Necessary:

• If √63 is not directly available, use values around it to estimate.

These methods help you find the value of √63, with varying degrees of precision and computational effort.

Square Root of 63 by Long Division Method

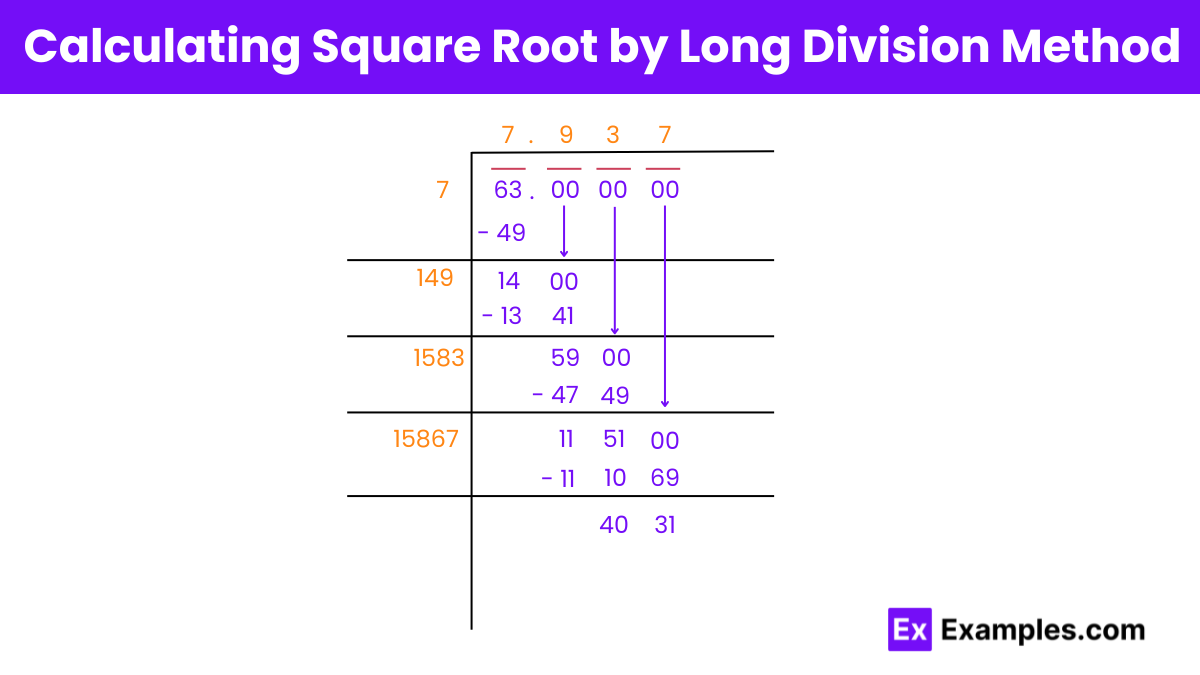
Step 1: Pair the Digits

• Place a bar over the number 63, starting from the one’s place, to create pairs. For 63, it’s just 63. Represent this inside the division symbol.

Step 2: Find the Initial Divisor

• Identify the largest number that, when multiplied by itself, gives a product less than or equal to 63. The number 7 works since (7 × 7 = 49), which is less than 63. Now, divide 63 by 7.

Step 3: Introduce Decimal Point and Zero Pairs

• After the initial division, place a decimal point in the quotient and add pairs of zeros to continue the division. Multiply the current quotient (7) by 2, resulting in 14, which becomes the starting digits of the new divisor.

Step 4: Find the Next Digit

• Determine the largest digit to place in the unit’s position of the new divisor (140X) such that the product is less than or equal to 1400. The number 9 fits because (149 × 9 = 1341). Subtract 1341 from 1400 to get the remainder and bring down the next pair of zeros.

Step 5: Repeat the Process

• Continue by bringing down pairs of zeros. Multiply the current quotient (79, ignoring the decimal point) by 2, resulting in 158. This forms the starting digits of the new divisor.

Step 6: Determine the Next Digit

• Choose the largest digit for the new divisor (158X) such that its product is less than or equal to the remainder plus the next pair of zeros. For example, 3 works because (1583 \times 3 = 4749). Subtract 4749 from 5900 to get the new remainder.

Step 7: Continue the Division

• Keep adding pairs of zeros, finding the new digit for the divisor, and performing the division as described in the previous steps until you reach the desired level of accuracy.

63 is Perfect Square root or Not

A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In other words, a perfect square is the square of an integer. For example, 4, 9, 16, 25, etc., are perfect squares because they can be expressed as 2², 3², 4², 5², etc.

However, the number 63 cannot be expressed as the square of an integer. Therefore, it is not a perfect square.

FAQs

What is the simplified form of √63?

The simplified form of √63 is 3√7.

A factor of 63 is any number that divides evenly into 63, such as 1, 3, 7, 9, 21, and 63.63 is not a prime factor because it can be divided by other numbers besides 1 and itself. Its prime factors are 3 and 7.

What is a factor of 63?

A factor of 63 is any integer that divides 63 without leaving a remainder. For example, the factors of 63 are 1, 3, 7, 9, 21, and 63.

What is 63 a prime factor?

63 is not a prime factor because it can be divided by other numbers besides 1 and itself. However, its prime factors are 3 and 7.