Square & Square Root of 68

In the realm of mathematics, particularly in algebra, understanding squares and square roots is vital. When we square the number 68 by multiplying it by itself, we get 4,624. This operation not only illustrates the basic principles of multiplication but also sheds light on the behavior of numbers, distinguishing between rational and irrational types. By examining the square and square root of 68, we deepen our insight into mathematical relationships and patterns, paving the way for more sophisticated mathematical concepts and problem-solving strategies. This foundational knowledge is crucial for both academic studies and practical applications.

Square of 68

68²(68 × 68) = 4,624

The square of a number is obtained by multiplying the number by itself. In the case of 68, when we square it, we perform the calculation 68×68. This multiplication yields a product of 4,624. Squaring is a fundamental operation in mathematics that helps to build a deeper understanding of algebraic expressions and functions.

Square Root of 68

√68 = 8.246

The square root of a number is a value that, when multiplied by itself, yields the original number. The square root of 68, denoted as √68, is an irrational number because it cannot be expressed as a simple fraction, and its decimal representation is non-repeating and non-terminating.

Square Root of 68: 8.246

Exponential Form of 68: (68)^½ or  or (68)^0.5 

Radical Form of 68: √68

Is the Square Root of 68 Rational or Irrational?

The square root of 68 is Irrational

Rational:

The square root of 68 is not a rational number. A rational number is one that can be expressed as a fraction with integer in the numerator and the denominator, or as a repeating or terminating decimal. The square root of 68 does not meet these criteria, as it cannot be expressed as a fraction of two integers.

Irrational:

The square root of 68 is an irrational number. Irrational numbers are those that cannot be precisely expressed as a simple fraction, and their decimal representation is non-repeating and non-terminating. The square root of 68, approximately 8.246, continues indefinitely without repeating, fitting the definition of an irrational number. These numbers play a vital role in mathematics, offering unparalleled precision in various calculations and contributing to theoretical foundations in algebra and geometry.

Method to Find Value of Root 68

1. Using a Calculator

The most straightforward and precise method for most uses is simply using a calculator. Most calculators can provide the square root of any number, giving you an accurate decimal approximation almost instantaneously.

2. Estimation

You can estimate the square root of 68 by identifying numbers whose squares are close to 68. For instance, since 8²=64 and 9²=81, you know that √68 lies between 8 and 9. Fine-tuning this estimate, you might guess √68 is around 8.2 to 8.3, as these squared are close to 68.

3. Newton-Raphson Method

This numerical method is useful for finding better approximations of the roots of real-valued functions. For √68, you can use the function 𝑓(𝑥)=𝑥²−68f(x)=x²−68. The Newton-Raphson formula is:

𝑥_𝑛+1=𝑥_𝑛−𝑓(𝑥_𝑛)𝑓′(𝑥_𝑛)=𝑥_𝑛−𝑥𝑛²−68/2𝑥_𝑛

Starting with an initial guess (e.g., 8), you iterate this formula until the changes between successive guesses are minimal.

4. Babylonian Method (Heron’s Method)

This ancient algorithm is another way to find square roots and is very similar to the Newton-Raphson method:

• Start with an initial guess, 𝑥0​ (e.g., 8).
• Use the iterative formula: 𝑥_𝑛+1=1/2(𝑥_𝑛+68_𝑥𝑛)
• Repeat the process until the value stabilizes.

5. Exponential and Logarithmic Functions

If you have access to a scientific calculator or software that can handle exponents and logarithms, you can find the square root using these functions:

√68=𝑒^1/2log⁡(68)

Square Root of 68 by Long Division Method

Calculating the square root of 68 using the long division method involves a detailed step-by-step process that breaks down the number systematically to find its square root. This method is particularly useful when you need a decimal approximation of the square root and do not have access to a calculator. Here’s how you can calculate the square root of 68 using the long division method:

Step-by-Step Calculation of √68 Using the Long Division Method

1. Set up the number under a square root bracket: Place the number 68 under the square root symbol. Since 68 has no decimal, you work with it as is.
2. Pair the digits from right to left:
   • Since 68 is less than 100, consider it as 68.00, and pair from right to left. You pair 68 as (68).
3. Find the largest number whose square is less than or equal to the first pair:
   • The first pair here is 68. The largest whole number whose square is less than or equal to 68 is 8 because 8²=64
4. Subtract the square of the number from the first pair and bring down the next pair:
   • Subtract 64 from 68, which gives 4. Now bring down the next pair (00), making it 400.
5. Double the divisor and choose a new digit in the dividend:
   • The current divisor is 8. Double it to get 16. Now, find a digit ‘X’ such that (160 + X)X is less than or equal to 400.
   • The best fit for ‘X’ here is 2 since 162×2=324
6. Subtract and find the remainder:
   • Subtract 324 from 400, leaving a remainder of 76.
7. Repeat the process with more decimal places if higher precision is needed:
   • Bring down another pair of zeros (making the new remainder 7600), double the latest result of the divisor (162) to get 324, and repeat the process to find the next digit.
   • Continuing in this manner, you can find more digits of the square root of 68.

68 is Perfect Square root or Not?

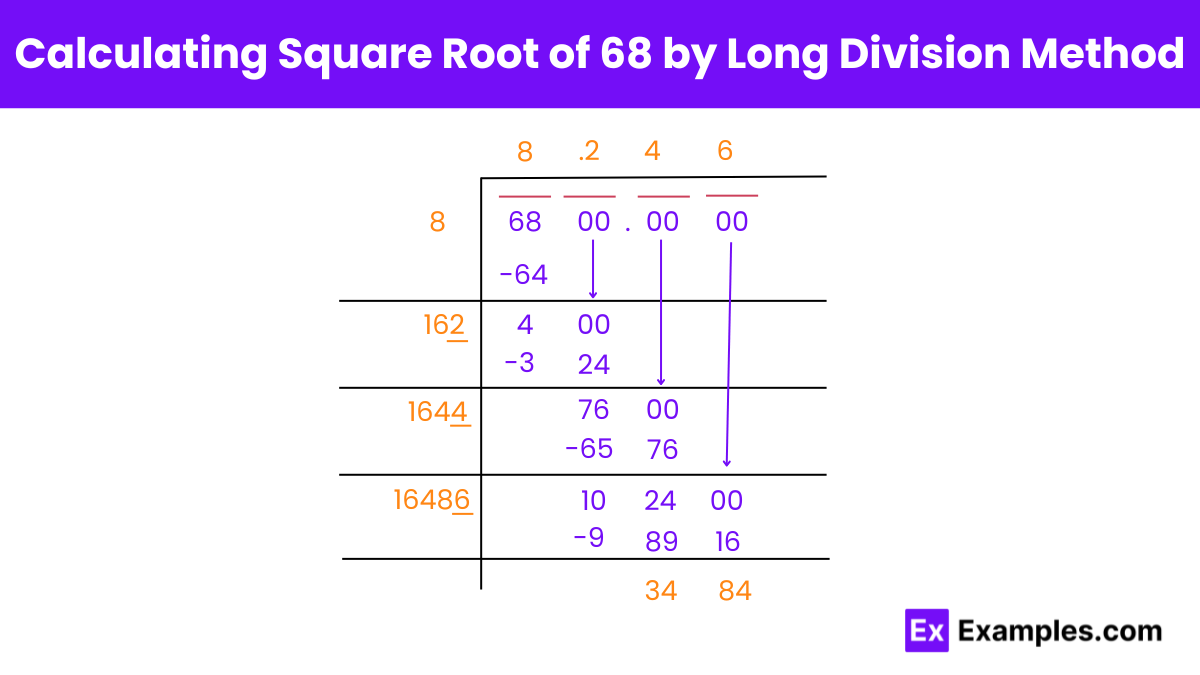
No, 68 is not a perfect square

No, 68 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. The square root of 68, approximately 8.246, is not an integer, indicating that 68 cannot be expressed as the square of any whole number. Hence, it is not a perfect square.

FAQS

Can the square root of 68 be a negative number?

Yes, the square root of any positive number has two values: one positive and one negative. Thus, the square root of 68 can also be -8.246, although the principal square root (commonly referred to in most contexts) is 8.246.

Are there any quick tips or tricks to estimate the square root of 68?

A quick estimate can be made by knowing squares of numbers close to 68. For example, since 8² = 64 and 9² = 81, it’s clear that √68 is slightly more than 8.

How can errors be minimized when calculating the square root of 68 manually?

Errors can be minimized by carefully performing each step in the long division method or using estimation techniques. Double-checking each step and using additional pairs of zeros can also help achieve more accurate results.

How accurate are calculators at computing the square root of 68?

Calculators are typically very accurate when computing the square root of numbers like 68, providing values to several decimal places. The level of accuracy depends on the calculator’s design and the algorithms it uses.

Can the square root of 68 be simplified?

Since 68 is not a perfect square and does not have square factors, its square root cannot be simplified into a simpler radical form.