Square & Square Root of 77

In the domain of mathematics, particularly within algebraic studies, the foundational principles of squares and square roots stand as paramount. Squaring a number, such as taking 77 and multiplying it by itself to yield 5929, is a fundamental operation. This process serves as a cornerstone in exploring the properties inherent in both rational numbers (expressible as a fraction of two integers) and irrational numbers (which defy expression as a neat fraction). Understanding these fundamental concepts enriches one’s comprehension of mathematical relationships and patterns, fostering a deeper insight into the subject’s intricacies.

Square of 77

77² (77 × 77) = 5929

A square number, exemplified by the square of 77, results from multiplying a number by itself. In this case, squaring 77 yields 5929. These numbers play a fundamental role in mathematics, serving as building blocks for understanding various mathematical concepts and relationships.

Square Root of 77

√77 = 8.77496438739

Or

√77 = 8.774 Upto 3 decimals

The square root of a number, such as the square root of 5929, reveals the original number that, when multiplied by itself, yields the given square. In the case of 77 squared, its square root is 77, indicating the number that produces 5929 when squared.

Square Root of 77: 8.77496438739

Exponential Form: 77^½ or 77^0.5

Radical Form: √77

Is the Square Root of 77 Rational or Irrational?

The square root of 77 is an irrational number

The square root of 77 is an irrational number because it cannot be expressed as a fraction of two integers. It is a non-repeating, non-terminating decimal. This classification aligns with the general property of square roots of non-perfect squares being irrational.

Rational Number:
A rational number can be expressed as a fraction of two integers, denoted as a/b, where b isn’t zero. Examples include positive, negative, or zero values, like 3/4, -5/2, 0, 1, -2, etc.

Example: For instance, 3/4 is rational as both 3 and 4 are integers, and the denominator isn’t zero.

Irrational Number:
An irrational number, such as √2 or π, cannot be expressed as a fraction of two integers. Its decimal expansion neither ends nor repeats, thus defying representation as a/b.

Example: Consider √2; its decimal expansion (√2 ≈ 1.41421356…) is non-repeating and non-terminating, making it irrational.

Method to Find Value of Root 77

Finding the exact value of the square root of 77 can be challenging because it is an irrational number. However,

you can approximate its value using various methods such as the Babylonian method or numerical methods like Newton’s method. Here’s a brief explanation of the Babylonian method:

Initial Guess: Start with a reasonable initial guess. A common choice is to start with half of the number you’retrying to find the square root of, so for √77, you could start with around 8.5 because 8.5² is 72.25, which is close to 77.

Iteration: Use the formula (xⁿ⁺¹ = 1/2 xₙ + S/xₙ) where (xₙ) is the current guess and (S) is the number you’re finding the square root of (in this case, 77). Repeat this formula with the initial guess to get a better approximation.

Repeat: Keep applying the formula until you reach a desired level of accuracy or until the approximation stops changing significantly.

This method converges relatively quickly to the actual value of the square root.

Square Root of 77 by Long Division Method

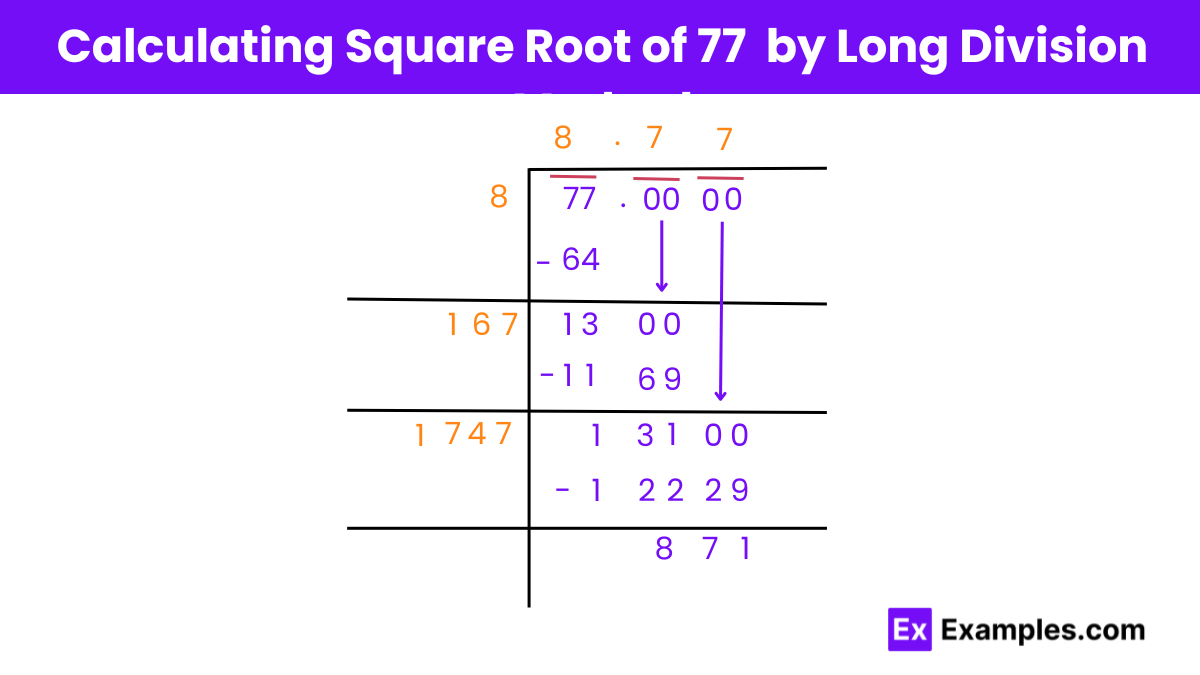
Sure, here’s a breakdown of the steps to find the square root of 77 using the long division method, organized into subheadings:

Step 1: Pairing Digits

Starting from the right, pair up the digits of 77 by placing a bar above them.

• Also, pair up the 0s in the decimal part from left to right.

Step 2: Finding the First Digit

Find a number that, when multiplied by itself, gives a product less than or equal to 77.

The number 8 fits here as (8² = 64).

Divide 77 by 8, giving a quotient of 8 and a remainder of 13.

Step 3: Bringing Down the Next Pair of Digits

Drag a pair of 0s down and place them next to the remainder (13) to make the new dividend 1300.

Step 4: Doubling the Divisor

Double the divisor (8) to get 16 and enter it below with a blank digit on its right.

Think of a number that is greater than or equal to the dividend, i.e., 1300.

167 is a suitable number to divide 1300.

Step 5: Finding the Next Digit

Multiply 167 by 7 ((167 × 7 = 1169 < 1300)) and write the product below.

Subtract the product from 1300, leaving a remainder of 131.

Step 6: Repeat Until Desired Precision is Achieved

Repeat the process until you get the desired level of accuracy in your approximation of the square root of 77.

Following these steps systematically will help you find the square root of 77 using the long division method.

77 is Perfect Square root or Not?

No, 77 is not a perfect square number

No, 77 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since the square root of 77 is not an integer (it’s approximately 8.774964387), 77 is not a perfect square.

FAQs