What is the square of 800?
640,000
560,000
720,000
640,800
of 10
Square & Square Root of 800 – Methods, Calculation, How to find
Square & Square Root of 800 – Methods, Calculation, How to find
In the realm of mathematics, particularly within algebra, the significance of squares and square roots cannot be overstated. These concepts form the bedrock upon which our understanding of rational and irrational numbers is built. By taking a number like 800 and squaring it, we illustrate the fundamental nature of this operation, paving the way for deeper exploration of mathematical relationships and patterns.
Square of 800
A square number such as 800 arises from multiplying an integer by itself. The square of 800 equals 640,000, highlighting algebraic principles and enriching comprehension of mathematical relationships and patterns within algebraic studies and beyond.
Square Root of 800
or
√800 ≈28.284 upto 3 decimals
The square root of 800 is approximately 28.2842712. Mastery of square roots involves identifying the number that, when multiplied by itself, equals 800. This understanding is crucial for exploring algebraic relationships and patterns within mathematics.
Exponential Form: 800^1/2 or 800^0.5
Radical Form: √800
Is the Square Root of 800 Rational or Irrational?
Rational Numbers: Rational numbers are expressible as fractions of two integers.
Irrational Numbers: Irrational numbers cannot be expressed as fractions of integers.
As the square root of 800 is not a perfect square, it is irrational. It cannot be expressed as a simple fraction.
Methods to Find the Value of Root 800
- Estimation Method: Begin with an initial approximation and refine it iteratively using methods like Newton-Raphson.
- Prime Factorization Method: Express 800 as a product of prime factors, then find the square root of each prime factor.
- Calculator: Utilize a calculator with a square root function to directly compute the square root of 800.
Square Root of 800 by Long Division Method
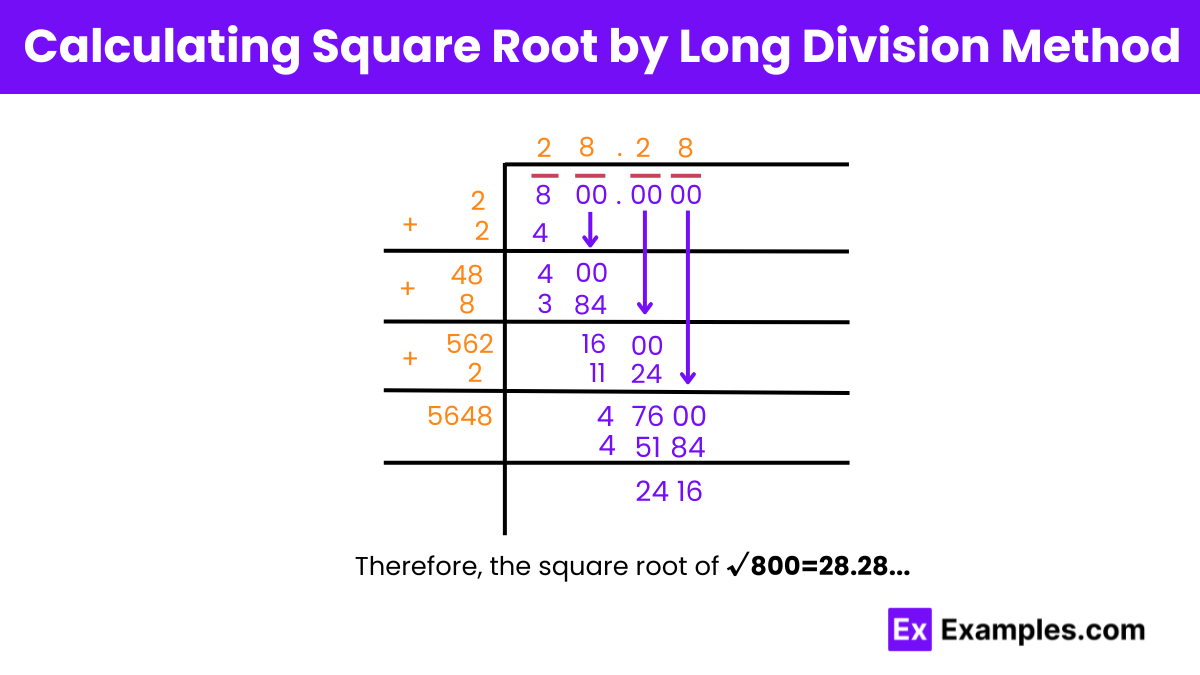
Step 1: Starting from the right, pair up the digits of 800 by placing a bar above 00 and 8 separately. Also, pair the 0s in the decimal part in pairs of 2 from left to right.
Step 2: Find a number that, when multiplied by itself, gives a product less than or equal to 8. This will be 2, so place 2 in the quotient and the divisor’s place, resulting in a remainder of 4.
Step 3: Drag down 00 beside the remainder, making it 400. Add the divisor to itself and write it below (2 + 2 = 4).
Step 4: Find a number X such that 4X × X results in a number less than or equal to 400. The number 8 works here, so place 8 next to the divisor and in the quotient, making the new divisor 48.
Step 5: Find the remainder and drag down the pair of 0s from the decimal part of the number. Add X to the divisor, making the new divisor 56.
Continue in this manner to get the desired decimal places.
800 is a Perfect Square or Not
800 is not a perfect square because it cannot be expressed as the product of an integer multiplied by itself. In other words, there is no integer such that its square equals 800.
FAQs
What is 800 in multiples?
The multiples of 800 are 800, 1600, 2400, 3200, 4000, 4800, 5600, 6400, 7200, and 8000. These are obtained by multiplying 800 by integers 1 through 10.
Is 800 divisible by any square numbers?
Yes, 800 is divisible by 4, 16, 25, and 100.
What are the prime factors of 800?
The prime factors are 2⁵×5²
Share :
Practice Test
What is the square root of 800 rounded to the nearest tenth?
28.1
28.2
28.3
28.4
of 10
Which number multiplied by itself gives a product closest to 800?
28
29
30
31
of 10
If 800 is divided by its square root, what is the result?
20
25
28.28
32
of 10
The square of a number is 640,000. What is that number?
500
600
700
800
of 10
How many times does the square root of 800 go into 800?
25
26
27
28
of 10
If y = 800, what is y²?
640,000
620,000
660,000
680,000
of 10
The area of a square is 640,000 square units. What is the length of one side of the square?
700 units
750 units
800 units
850 units
of 10
What is the square root of 800 expressed as a decimal?
28.25
28.28
28.29
28.30
of 10
What is the square of 800 divided by 4?
150,000
160,000
170,000
180,000
of 10