What is the square of 82?
6722
6724
6726
6728
of 10
Square & Square Root of 82 – Methods, Calculation, How to find
Square & Square Root of 82 – Methods, Calculation, How to find
In mathematics, especially in algebraic studies, squares and square roots are fundamental. Squaring a number, such as 82, involves multiplying it by itself to get 6724, a key operation. It’s crucial for exploring properties of rational (expressible as fractions) and irrational numbers (not neat fractions). Understanding these concepts enriches comprehension of mathematical relationships and patterns. Squares reveal how numbers interact, forming the basis of algebraic analysis. Likewise, square roots unveil the origin of numbers, shedding light on their nature and significance within mathematical frameworks. Mastering these concepts enhances one’s mathematical prowess and analytical skills.
Square of 82
A square number, like 82, is obtained by multiplying a number by itself. The square of 82 equals 6724. Understanding square numbers elucidates their role in algebraic analysis, showcasing their significance in mathematical patterns and relationships, essential for comprehending fundamental mathematical concepts and their applications.
Square Root of 82
Or
√82 ≈ 9.055 Up to 3 decimals
The square root of 82, when squared, equals 82. It’s the number that, when multiplied by itself, gives 82. The square root, approximately 9.055, unveils the origin of 82. Understanding square roots elucidates their role in algebraic analysis, showcasing their significance in mathematical patterns and relationships.
Exponential Form: 82^1/2 or 82^0.5
Radical Form: √82
Is the Square Root of 82 Rational or Irrational?
This is because it cannot be expressed as a fraction of two integers. It is approximately equal to 9.05538513814, and its decimal representation goes on indefinitely without repeating or terminating.
Rational Number : A rational number is expressible as a fraction of two integers, where the denominator is non-zero.
Irrational Number : An irrational number is a real number that cannot be expressed as a ratio of two integers
Methods to Find Value of Root 82
Prime Factorization Method: Express 82 as a product of prime factors and group pairs of similar factors to find the square root of 82.
Estimation Method: Make an initial estimate (e.g., 9) and square it (81). Adjust the estimate based on whether the square is greater or less than 82, refining the estimate until it’s close enough.
Long Division Method: Perform long division to find the square root iteratively, similar to the traditional long division method.
Newton’s Method: Utilize iterative approximation using Newton’s method, which involves refining guesses based on the tangent line to the function curve.
Calculator or Software: Use a calculator or mathematical software capable of computing square roots directly.
Square Root of 82 by Long Division Method
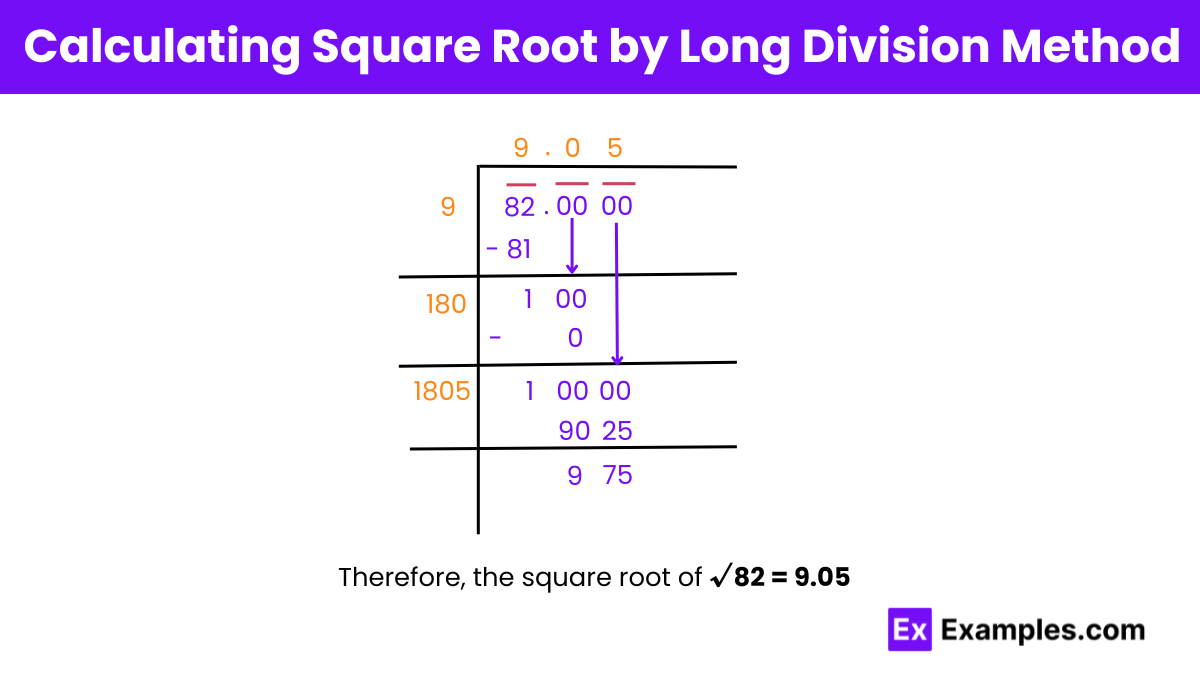
Step 1: Place a bar over every pair of digits of the number starting from the unit’s place (right-most side). We will have 1 pair, i.e., 82. After 82, we can add zeroes with a decimal point.
Step 2: Divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair (9 × 9 = 81).
Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor (9 + 9 = 18). Find a suitable number for the new divisor (180) for the new dividend (100).
Step 4: The new number in the quotient will be the same as selected in the divisor (180 × 0 = 0). It should be either less or equal to that of the dividend (180 > 100).
Step 5: Continue this process further using a decimal point and adding zeros in pairs to the remainder.
Step 6: The quotient obtained will be the square root of the number.
82 is Perfect Square root or Not
82 is not a perfect square because it cannot be expressed as the square of an integer. Its square root is an irrational number, approximately equal to 9.05538513814
FAQs
Which number is closest to the square root of 82?
The number closest to the square root of 82 is 9, as it is the integer closest to the square root of 82, which is approximately 9.055.
What is the factor of 82?
The factors of 82 are 1, 2, 41, and 82.
Is 82 divisible by?
82 is divisible by 1, 2, 41, and 82.
Why is 82 a prime number?
82 is not a prime number because it has factors other than 1 and itself, namely 2 and 41.
Share :
Practice Test
What is the square root of 6724?
81
82
83
84
of 10
Which of the following numbers is closest to the square root of 82?
8.9
9
9.1
10
of 10
What is the approximate square root of 82 to the nearest whole number?
8
9
10
11
of 10
The square of which of the following is closest to 82?
8
9
10
11
of 10
What is the value of √82 in decimal form rounded to two decimal places?
9.04
9.05
9.10
9.20
of 10
If x² = 82, what is the value of ?
9
8.5
9.05
9.1
of 10
If the square of a number is 82, what is the number?
8.5
9
9.05
9.1
of 10
What is the nearest perfect square to 82?
81
64
100
121
of 10
Which of the following is not a square root of 82?
9.05
9
8.9
9.1
of 10