Square & Square Root of 84

In the vast domain of algebraic mathematics, the fundamental concepts of squares and square roots are pivotal. Squaring a number, as demonstrated with 84 yielding 7056, stands as a cornerstone operation. It’s integral in exploring the properties of rational (expressible as a fraction) and irrational numbers (resistant to neat fraction representation). Understanding these bedrock principles enhances comprehension of mathematical relationships and patterns. These concepts delve into the essence of numbers, illuminating their intrinsic properties and behaviors within equations and functions. Mastery of squares and square roots extends beyond mere calculation; it fosters a deeper appreciation for the elegance and interconnectedness within the realm of mathematics.

Square of 84

84²(84 × 84) = 7056

A square number results from multiplying an integer by itself. The square of 84, calculated by multiplying 84 by 84, equals 7056. Understanding square numbers elucidates fundamental mathematical principles and lays the groundwork for exploring algebraic concepts, serving as a cornerstone in mathematical inquiry and problem-solving.

Square Root of 84

√84 = 9.16515138991

Or

√84 = 9.165 Upto 3 decimals

The square root of 84, approximately 9.165, represents the number that, when multiplied by itself, equals 84. Understanding square roots is essential in mathematics, aiding in solving equations and grasping numerical relationships. It unveils the inverse operation to squaring, pivotal in both algebraic and geometric contexts for calculations and problem-solving.

Square Root of 84 : 9.16515138991

Exponential Form : 84^½ or 84^0.5

Radical Form : √84

Is the Square Root of 84 Rational or Irrational?

The square root of 84 is irrational.

The square root of 84 is an irrational number. This means it cannot be expressed as a simple fraction of two integers. It is a non-repeating, non-terminating decimal, indicating its irrational nature.

Rational Number:
A rational number is any number that can be expressed as a fraction, where both the numerator and denominator are integers, and the denominator is not zero. It is typically denoted in the form (a/b). Examples include 3/4, -5/2, 0, 1, and -2. For instance, 3/4 qualifies as a rational number because it consists of integers as its numerator and denominator, with the denominator being non-zero.

Irrational Number:
An irrational number is a number that cannot be represented as a simple fraction of two integers. Its decimal representation is both non-terminating and non-repeating. Notable examples include √2, π (pi), and φ (phi). For instance, √2 is irrational because its decimal expansion (approximately 1.41421356…) continues indefinitely without exhibiting any repetitive pattern.

Method to Find Value of Root 84

To find the square root of 84, you can use various methods:

Prime Factorization Method: Decompose 84 into its prime factors (2² × 3 × 7). Then, pair the prime factors and take one from each pair (2 × 3 = 6). The product is the square root of 84.

Estimation Method: Approximate the square root of 84 by considering perfect squares near it (e.g., √81 = 9, √100 = 10). Interpolate between these values to get a close approximation.

Calculator: Use a calculator with a square root function to directly find the square root of 84. This provides a precise value without needing manual calculations.

Newton’s Method: Utilize iterative approximation methods such as Newton’s method to converge towards the square root of 84 through successive calculations based on initial guesses.

These methods offer different levels of precision and complexity, allowing flexibility in choosing the most suitable approach based on the requirements.

Square Root of 84 by Long Division Method

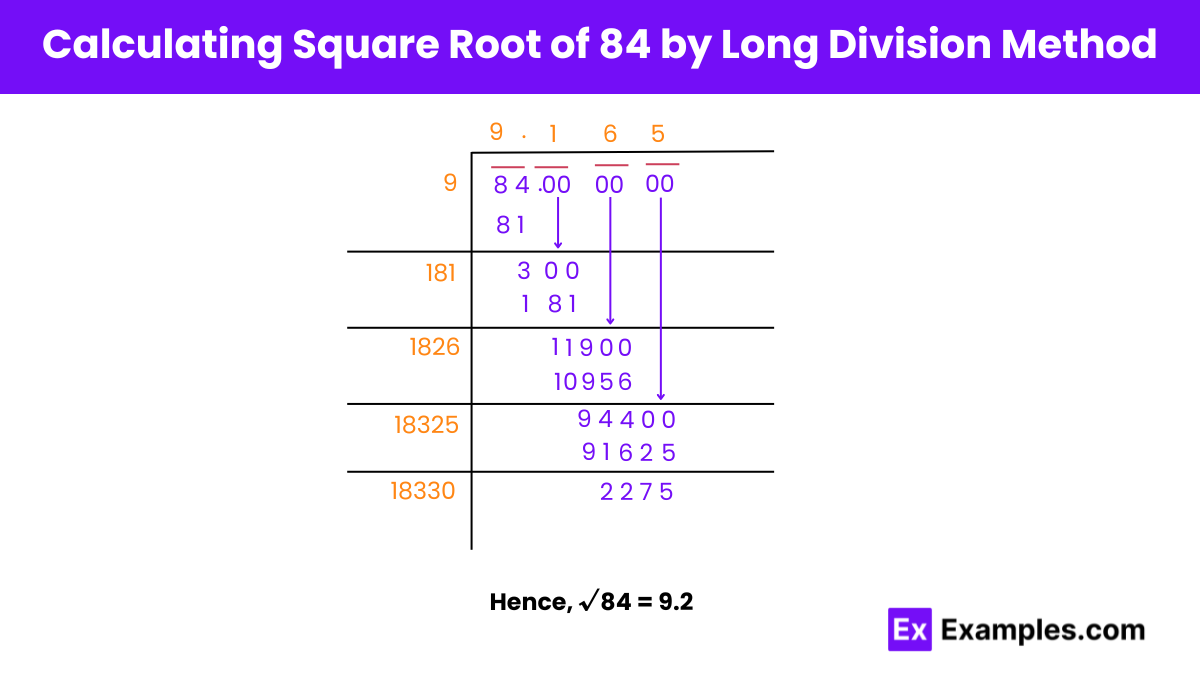
Square Root of 84 by Long Division Method

Dividend Setup: Write 84 as 84.0000. Identify a number × number that gives a product of 84 or less.

Initial Quotient: Determine 9 × 9 = 81. Subtract this from 84 to obtain a remainder of 3. Bring down the next pair of zeros (300).

Doubling the Quotient: Double the quotient (9) to get 18. Determine 18x × x ≤ 300.

Next Iteration: Identify 181 × 1 = 181. Subtract this from 300 to obtain a remainder of 119. Bring down the next pair of zeros (11900).

Further Iteration: Double the quotient (9.1) to get 182. Determine 182x × x as the new divisor.

Final Iteration: Determine 1826 × 6 = 10956. Subtract this from 11900 to get a remainder of 944. Bring down the next pair of zeros.

Repeat Process: Continue iterations until the quotient is approximated to 3 decimal places.

Result: √84 ≈ ±9.165.

84 is Perfect Square root or Not?

No, 84 is not a perfect square.

No, 84 is not a perfect square because it cannot be expressed as the square of an integer. The square root of 84 is approximately 9.165, which is not a whole number. In other words, there is no integer value that, when squared, equals 84.

FAQs

What is the significance of the square root of 84 in mathematics?

The square root of 84 is important in mathematics as it represents a fundamental concept in algebra and number theory. It illustrates the relationship between a number and its square root and is utilized in various mathematical calculations and problem-solving scenarios.

Can the square root of 84 be simplified further?

No, the square root of 84 cannot be simplified further because it is an irrational number, meaning it cannot be expressed as a simple fraction or in radical form with integers.

How is the square root of 84 used in real-life applications?

The square root of 84 can be used in practical applications such as calculating distances, areas, or volumes in geometry, engineering, physics, and other scientific fields where measurements and calculations involving squares and square roots are required.